Конспект лекций Глазова / 5.2. Среднее от ф-ции по анс арг

5.2. Среднее от функции по ансамблю аргументов.

В дальнейшем рассматривается частный случай, когда и аргументы и функции - непрерывные случайные величины. Говорят, что значения случайной величины Х (в общем случае - многомерной) составляют ансамбль. Геометрически ансамбль задается точками в пространстве (в общем случае - многомерном) значений.

Определение. Пусть имеется функция Y=(X) (в общем случае - векторного) случайного аргумента. Средним по ансамблю аргументов значением функции Y (или просто средним значением Y) называется (в общем случае - векторная) величина

M(Y)=M[(X)]=.

(5.2.1)

Это векторное равенство эквивалентно k скалярным равенствам, где k - размерность Y. В частном случае одномерной Y (k=1) получаем одно скалярное равенство

M(Y)=M[(X)]=(x)fx(x)dx.

(5.2.2)

Если аргумент тоже одномерный, то среднее значение функции Y

M(Y)=M[(X)]=(x)fx(x)dx.

(5.2.3)

M(Y) есть ничто иное, как математическое ожидание m_y , только оно найдено не по определению

my=,

(5.2.4)

а усреднением по ансамблю аргумента Х. Разница вычислений по (5.2.3) и по (5.2.4) принципиальна: если плотность f_x(x) аргумента известна, то этого достаточно для вычисления m_y по (5.2.3), а для вычисления по (5.2.4) необходимо знать плотность величины Y; как мы увидим в дальнейшем, вычисление плотности функции по плотности аргумента возможно, но это более сложная задача, чем вычисление среднего от функции, особенно в многомерном случае. Другими словами, для вычисления среднего от функции случайных аргументов нет необходимости сначала находить распределение этой функции, достаточно знать распределение аргументов. То же самое в еще большей степени относится к случаю, если и аргумент и функция многомерны, т. к. нахождение многомерного распределения функции по многомерному распределению аргументов представляет собой, чаще всего, очень сложную, или даже неразрешимую, задачу. В этом случае

M(Y)=(m_y1, m_y2, ..., m_yk),

- вектор математических ожиданий k-мерной СВ Y.

Букву M (в одномерном случае - букву M) в выражениях типа M[(X)] можно понимать как обозначение оператора усреднения; его действие называется усреднением функции случайных аргументов (или просто усреднением); алгоритм усреднения функции - «умножение на плотность аргументов и интегрирование». Полезно заметить, что усреднение - это взвешивание функции с весом плотности аргументов.

Использование оператора усреднения как такового вместо громоздких интегралов часто существенно сокращает выкладки. Это станет возможным, если заметим, что, как следует из интегрального представления (5.2.1), это линейный оператор:

M[a1(x)+a2(x)]=a1M[(x)]+a2M[(x)],

(5.2.5)

где а₁, а₂ - постоянные.

Среднее от функции случайных аргументов - фундаментальное понятие теории вероятностей. Глубокое осознание этого понятия требует математического аппарата, выходящего за рамки данного курса. Но и на элементарном уровне важность этого понятия видна уже из того, что почти все статистические характеристики и аргументов и функции (как числовые, так и функциональные) можно (и полезно) интерпретировать в терминах этого понятия. Покажем это на примерах, взяв для простоты случай одномерной функции одного аргумента.

• Плотность вероятности случайной величины Х:

  f_x(x)=

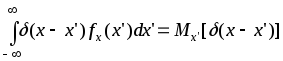
  (среднее параметрически зависит от х), (.) - дельта-функция.

• Функция распределения случайной величины Х:

F_x(x)=,

где - характеристическая функция интервала (, х) (не путать с характеристической функцией случайной величины):

(среднее параметрически зависит от х).

• Характеристическая функция величины X:

.

• Характеристическая функция величины Y=(X):

.

• Начальный момент порядка k случайной величины X:

.

• Центральный момент порядка k случайной величины Х:

• Начальный момент порядка k случайной величины Y=(X):

  .

• Центральный момент порядка k случайной величины Y=(X):

.