Конспект лекций Глазова / 5.4.2 Распр одном ф-ции двух аргум

5.4.2. Распределение одномерной функции

двух случайных аргументов.

Постановка задачи: пусть X и Y составляют двумерную систему случайных величин с известной плотностью f(x, y), а величина Z связана с ними известной функцией Z=(X, Y) двух переменных; требуется найти распределение величины Z.

Найдем сначала функцию распределения величины Z, а затем ее плотность вероятности. По определению

.

Последняя вероятность может быть вычислена, по общему правилу, интегрированием плотности f(x, y) в плоскости XOY по области D, во всех точках которой выполняется неравенство

,

(5.4.14)

т. е.

.

(5.4.15)

Плотность вероятности величины Z находим дифференцированием:

.

Практически область D находится следующим образом: рассматривается граничная кривая в плоскости XOY

;

(5.4.16)

эта кривая разбивает плоскость XOY на две или более подобластей, одна часть которых удовлетворяет неравенству (5.4.14), другая - противоположному неравенству. Интеграл (5.4.15) берется по всем подобластям, которые удовлетворяют неравенству (5.4.14). Например, если кривая (5.4.16) - окружность, то областью D, в зависимости от вида функции (.), является или круг, ограниченный этой окружностью, или вся плоскость XOY за исключением этого круга.

Т. о. общий алгоритм решения задачи нахождения распределения одномерной функции двух случайных аргументов таков: а) записывается уравнение (5.4.16) граничной кривой; б) находится область D; в) интегрированием по (5.4.15) находится F_y(y); г) дифференцированием находится f_y(y).

До сих пор не конкретизировались ни функция (.,.), ни плотность f(x, y), в этом смысле получен общий результат поставленной задачи. Теперь в качестве полезных и поучительных упражнений рассмотрим некоторые частные случаи, конкретизируя сначала функцию (.,.), а затем и плотность f(x, y).

Сумма двух случайных величин. Пусть

Z= (X, Y)=X+Y,

а плотность f(x, y) произвольна. Уравнение (5.4.16) граничной «кривой» принимает вид

x+y=z,

(5.4.17)

т. е. это прямая на плоскости XOY (см. рис. 5.4.2), составляющая угол 135⁰ с осью ОХ.

Рисунок 5.4.2.

Область D расположена левее-ниже этой прямой (на рис 5.4.2 заштрихована). Записав (5.4.17) в виде x=z-y, и выполняя внутреннее интегрирование в (5.4.15) по х, а внешнее - по у, имеем

;

(5.4.18)

Записав (5.4.17) в виде y=z-x, и выполняя внутреннее интегрирование в (5.4.15) по у, а внешнее - по х, имеем

.

(5.4.19)

Мы получили два разных выражения для одной и той же функции распределения; поскольку левые части равны, то равны и правые части.

Дифференцируя по z равенство (5.4.18), получаем

,

(5.4.20)

а дифференцируя по z равенство (5.4.19), получаем

.

(5.4.21)

Теперь мы получили два выражения для одной и той же плотности; поскольку левые части равны, то равны и правые части. Последние представляют собой два варианта записи свертки функции двух переменных. Тождество этих вариантов - известное в математике свойство. Заметим, что пока мы не предполагали независимости Х и Y, и в этом смысле рассматривали общий случай. Итак, плотность вероятности суммы двух случайных величин равна свертке двумерной плотности вероятности этих величин.

Разность двух случайных величин. Пусть Z= (X, Y)=X-Y. Граничная линия области D имеет уравнение х-у=z Это прямая на плоскости XOY (см. рис. 5.4.3), составляющая угол 45⁰ с осью ОХ. Область D находится выше-левее этой прямой (на рис. 5.4.3 заштрихована).

Рисунок 5.4.3.

Записывая интеграл в (5.4.15) двумя способами: сначала по х, затем по у, или сначала по у, затем по х, находим

.

Дифференцируя оба выражения по z, получаем

.

(5.4.22)

Сумма двух независимых случайных величин. Пусть опять Z=(X, Y)=X+Y, но теперь Х и Y независимы. Тогда их двумерная плотность факторизуется:

f(x, y)=fx(x)fy(y),

(5.4.23)

и подставляя это равенство в (5.4.20) и (5.4.21), находим:

.

Итак, плотность вероятности суммы двух независимых случайных величин равна свертке их плотностей.

Разность двух независимых случайных величин. Пусть опять Z=(X, Y)=X-Y, но теперь Х и У независимы. Подставляя (5.4.23) в (5.4.22), получаем

.

Произведение двух случайных величин. Пусть Z=XY. Граничная кривая имеет уравнение y=z/x и представляет собой при z>0 две ветви гиперболы, расположенные в первом и третьем квадрантах (см. рис. 5.4.4), а при z<0 - две ветви гиперболы, расположенные во втором и четвертом квадрантах. Область D заключена между этими ветвями (на рис 5.4.4 заштрихована).

Рисунок 5.4.4.

Интегрируя по этой области, при z>0 имеем:

.

Дифференцируя по z, находим

.

Аналогичный результат получится при z<0. В частном случае независимых X, Y при z>0 имеем

,

и аналогичный результат - при z<0.

Отношение двух случайных величин. Пусть Z=X/Y. Граничная кривая в плоскости XOY имеет уравнение y=x/z, и представляет собой прямую, проходящую через начало координат с угловым коэффициентом 1/z (см. рис. 5.4.5).

Рисунок 5.4.5.

Область D (на рис. 5.4.5 заштрихована) состоит из двух частей: ниже прямой при x<0, выше прямой при x>0. Интегрируя f(x, y) по этой области, имеем

.

Дифференцируя по z, получаем

.

В частном случае независимых X, Y имеем

.

Модуль двумерного случайного вектора. Пусть Z=. Если X и Y считать проекциями случайного вектора, то Z - модуль этого вектора. Пусть задана двумерная плотность f(x, y) проекций, найдем плотность f_z(z) модуля.

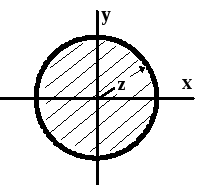
Рисунок 5.4.6.

Уравнение граничной кривой запишется в виде

x²+y²=z²,

т. е. область D - круг радиуса z (z0) с центром в начале координат (см. рис. 5.4.6; область D заштрихована). Интегрирование по этой области удобно провести в полярной системе координат. Полагая

,

имеем

Дифференцирование по z дает

.

(5.4.24)

В частном случае, когда Х и Y независимы, получаем

(5.4.25)

Модуль нормального двумерного случайного вектора с независимыми компонентами. Хотя это частный случай предыдущей задачи, именно этот случай важен в статистической радиотехнике и некоторых других приложениях. Задача сводится к подстановке в (5.4.25) одномерных плотностей величин Х, Y:

Чтобы несколько упростить задачу, сделаем еще одно предположение: . Подынтегральная функция в (5.4.25) равна

.

Обозначив m_x=a, m_y=b, и записав выражение в квадратных скобках в виде

z²+a²+b²-2z(acos+bsin),

подставляем в (5.4.25):

.

Этот интеграл не выражается конечной комбинацией элементарных функций и равен

,

где - модифицированная функция Бесселя первого рода нулевого порядка. В результате получаем

,

(5.4.26)

где

,

- модуль вектора математических ожиданий. Распределение (5.4.26) называется обобщенным распределением Рэлея или распределением Райса (см. рис. 5.4.7).

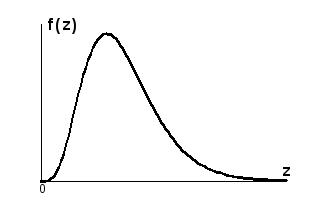
Рисунок 5.4.7.

Плотность вероятности распределения Райса.

В еще более частном случае, когда m_x=m_y=0, будет , и поскольку , получаем

.

(5.4.27)

Это важное в ряде приложений распределение Рэлея. Еще раз уточним, что оно получено как распределение модуля нормального двумерного вектора, компоненты которого независимы, имеют одинаковые дисперсии и нулевые математические ожидания. Кратко двумерное распределение компонент можно записать как

N(0, 0, ).

Рисунок 5.4.8.

Плотность вероятности распределения Рэлея при .

Обсудим поведение кривой плотности вероятности распределения Рэлея (см. рис. 5.4.8).

Дифференцируя (5.4.27) по z и приравнивая производную нулю, находим моду z_mod=; это равенство раскрывает смысл единственного параметра распределения . Плотность вероятности f_z(z) равна нулю при z<0, плавно нарастает до значения при , затем плавно убывает до нуля.

Функция распределения Рэлея равна

Обобщенные распределения. На практике часто бывает, что из измерений доступны числовые характеристики случайной величины, и требуется по ним оценить плотность вероятности; такого рода задачи решает математическая статистика, элементы которой изложены ниже. Для решения этой задачи нужно вначале выбрать класс плотностей, которому принадлежит искомая плотность. Для большей гибкости решения обычно выбирают класс с двумя или большим числом параметров. Такой класс можно назвать обобщенным распределением.

Три обобщенных класса можно получить как обобщения распределения Рэлея. Первый класс называется распределением Вейбула и имеет плотность вида

,

где А - коэффициент нормировки, равный, как нетрудно найти, а. Это распределение имеет два параметра а, , в зависимости от значений которых получаются другие, более простые распределения. При а=1 получаем

, >0,

т. е. экспоненциальное распределение. При а=2, =1/2² получаем распределение Рэлея.

Второй класс называется распределением Накагами и имеет плотность вида

,

где B - коэффициент нормировки, равный

.

Это распределение имеет два параметра m, . При получаем

,

т. е. одностороннее нормальное распределение; при m=1, получаем распределение Рэлея.

Третий класс называется гамма-распределением и имеет плотность вида

, >0,

где С - коэффициент нормировки, равный

.

Это распределение имеет два параметра n, , в зависимости от значений которых получаются другие, более простые распределения. В частности, при n=1 получается экспоненциальное распределение, при n=2 - распределение Рэлея.

5.4.3. Распределение одномерной функции

нескольких независимых случайных аргументов.

Мы рассмотрим этот вопрос на примере линейной функции нескольких случайных переменных. Пусть

Z=a₁X₁+a₂X₂+...+a_nX_n ,

и величины {X_k} (k=1, 2, ..., n) независимы. Применим метод характеристических функций (ХФ). ХФ непрерывной СВ Z, введенная в п. 3.6 как преобразование Фурье от плотности

,

может рассматриваться, согласно п. 5.2, как среднее вида

или

,

(5.4.28)

т. е. ХФ величины Z равна произведению ХФ величин Y_k=a_kX_k (k=1, 2, ..., n). При выводе формулы (5.4.28) учтено, что оператор усреднения линеен, и что среднее от произведения независимых (а следовательно, и некоррелированных) случайных величин равно произведению их средних.

Т. о. алгоритм вычисления плотности f_z(z) таков: а) находим ХФ величин Y_k=a_kX_k по правилу

;

б) перемножая их, находим ХФ величины Z; в) обратным преобразованием Фурье от нее находим плотность величины Z.

Пусть теперь все величины X_k - нормальные N(m_k, ) (k=1, 2, ..., n). Тогда все величины Y_k - нормальные N(a_km_k, ) и также независимы. Поскольку ХФ нормальной N(m, ) величины равна , то ХФ величины Y_k равна , и перемножая ХФ величин Y_k , получаем

,

что после введения обозначений

,

дает

,

имеющую вид ХФ нормальной величины. Т. о. мы получили важный результат: линейная функция независимых нормальных величин есть величина нормальная; ее средние и дисперсия соответствуют результатам, полученным в п. 5.3. На самом деле справедлив и гораздо более общий результат: n-мерная линейная функция m-мерной величины есть n-мерная нормальная случайная величина (независимость не предполагается).