Конспект лекций Глазова / 4.3. Механич интерпр распр

4.3. Механическая интерпретация распределений.

Для лучшего понимания статистических характеристик случайных величин полезна некоторая механическая аналогия. Рассмотрим ее отдельно для дискретных и непрерывных, одномерных и двумерных СВ.

Рассмотрим идеализированный жесткий тонкий стержень пренебрежимой массы, сопоставленный с осью координат, к которому в точках x₁, x₂,..., x_N (N - конечно или бесконечно) прикреплены грузики массой m₁, m₂,..., m_N , соответственно. Общая масса системы пусть равна 1 кг:

M==1.

(4.3.1)

Эта система дает механическую интерпретацию дискретного распределения в том смысле, что механические характеристики, по своей математической структуре, аналогичны статистическим характеристикам одномерной дискретной СВ, имеющей значения в тех же точках x₁, x₂, ..., x_N с вероятностями p_i=m_i при всех i. Действительно, равенство (4.3.1) аналогично условию нормировки (3.2.1); кусочно-постоянная функция «зависимость суммы масс не правее точки x от координаты этой точки» аналогична функции распределения СВ; суммарная масса участка (a, b] так же выражается через введенную функцию, как вероятность попадания СВ в тот же интервал - через функцию распределения; координата центра тяжести механической системы

аналогична математическому ожиданию СВ

;

момент инерции механической системы относительно начала координат

,

аналогичен второму начальному моменту ; момент инерции механической системы относительно центра тяжести

,

аналогичен второму центральному моменту и т. д.

Теперь рассмотрим идеализированный жесткий тонкий стержень, сопоставленный с осью координат, имеющий непрерывно распределенную линейную плотность массы (масса на единицу длины стержня) , и пусть общая масса стержня равна 1 кг:

M==1.

(4.3.2)

Эта система дает механическую интерпретацию непрерывного распределения в том смысле, что механические характеристики, по своей математической структуре, аналогичны статистическим характеристикам одномерной непрерывной СВ, имеющей плотность вероятности f(x)=. Действительно, равенство (4.3.2) аналогично условию нормировки (3.3.7) для непрерывной СВ; непрерывная неубывающая функция G(x), равная массе стержня левее точки x, аналогична (и даже равна) функции распределения F(x); масса участка [a, b]

M_{[a, b]}=G(b)-G(a),

так же выражается через функцию G(x), как вероятность попадания СВ на участок [a, b]:

P(X[a, b])=F(b)-F(a),

через функцию F(x); координата центра тяжести механической системы

,

аналогична математическому ожиданию СВ ; момент инерции механической системы относительно начала координат

W₀=,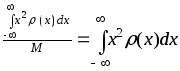

аналогичен второму начальному моменту ; момент инерции механической системы относительно центра тяжести

,

аналогичен второму центральному моменту и т. д.

Перейдем к интерпретации непрерывного двумерного распределения. Рассмотрим идеализированный жесткий тонкий лист, сопоставленный с двумерной декартовой системой координат, имеющий непрерывно распределенную поверхностную плотность массы (масса на единицу площади листа) , и пусть общая масса листа равна 1 кг:

=1.

(4.3.3)

Эта система дает механическую интерпретацию непрерывного двумерного распределения в том смысле, что механические характеристики, по своей математической структуре, аналогичны статистическим характеристикам двумерной СВ, имеющей плотность вероятности f(x, y)=. Действительно, равенство (4.3.3) аналогично условию нормировки

,

для непрерывной двумерной СВ; всюду непрерывная и всюду неубывающая функция G(x), равная массе «угла» с вершиной (x, y), аналогична (и даже равна) функции распределения F(x, y); масса произвольной области E

,

равна вероятности попадания случайной точки в эту же область:

;

координаты x_цт , y_цт точки центра тяжести листа

,

,

совпадают с частными математическими ожиданиями m_x , m_y ; момент инерции листа относительно оси OY

W_OY=,

равен частному второму начальному моменту СВ X ; момент инерции листа относительно оси OX

W_OX=,

равен частному второму начальному моменту СВ Y ; момент инерции листа относительно прямой, проходящей через центр тяжести листа параллельно оси OY,

,

равен частному второму центральному моменту СВ X ; момент инерции листа относительно прямой, проходящей через центр тяжести листа параллельно оси OX,

,

равен частному второму центральному моменту СВ Y и т. д.