Конспект лекций Глазова / 10. Испыт гипотез конкрет задачи

10. Испытание гипотез: конкретные задачи.

В п. 9 рассмотрены элементы общей теории испытания статистических гипотез. В данном пункте рассматриваются сравнительно простые и, в то же время, достаточно важные для приложений конкретные задачи испытания гипотез. Все они относятся к самому простому классу двухальтернативных испытаний простых гипотез, в котором достигнута полная теоретическая ясность.

10.1. Испытание простых гипотез

с нормальными распределениями.

Постановка задачи. Решающая статистика. Рассмотрим испытание гипотез Н₀: N(m₀, ) и Н₁: N(m₁, ), где m₀, m₁, известны. Это не самый общий случай простых нормальных гипотез, т. к. дисперсии в гипотезах одинаковы. Не ограничивая общности, можно считать, что =1 (например, можно перед испытанием гипотез разделить все выборочные значения на , или соответствующим образом изменить отношение правдоподобия и порог). Тогда Н₀: N(m₀, 1), H₁: N(m₁, 1), т. е. плотности одного выборочного значения в гипотезах:

,

,

плотности вероятности выборки в гипотезах:

отношение правдоподобия

.

Возводя круглые скобки в квадрат и приводя подобные, приводим выражение в квадратных скобках к виду:

[...]=,

а выражение для J(x) к виду:

.

(10.1.1)

Подставляя сюда выражение выборочного среднего

,

(10.1.2)

получаем

.

(10.1.3)

Любая комбинация выборочных значений называется статистикой. Мы получили решающую статистику, т. е. статистику, которую нужно сравнивать с порогом и принимать решения. Замечательно, что выборочные значения входят только в величину m*, которая есть однородная функция (т. е. сумма одинаковых степеней) выборочных значений. Такая величина называется достаточной статистикой. Не всякая задача испытания гипотез имеет достаточную статистику, но если она имеется, то предоставляет два преимущества:

1) решающее правило можно сформулировать как сравнение достаточной статистики с некоторым (уже другим) порогом; от этого решающее правило становится проще;

2) порог для достаточной статистики найти проще, чем для решающей статистики J, которая в общем случае не является однородной функцией выборочных значений.

Решающее правило. Переведем неравенство для решающей статистики J (см. (9.3.4))

J

(10.1.4)

в неравенство для достаточной статистики m*. Прологарифмировав (10.1.4) и решив полученное неравенство относительно m*, получим искомое неравенство:

(10.1.5)

где

.

(10.1.6)

Понятно, почему возникли два варианта: гипотезы отличаются только математическими ожиданиями генеральной СВ, и в этом смысле варианты симметричны с точностью до обозначений. Поэтому можно рассмотреть лишь один вариант. Выберем вариант m₀<m₁, тогда второе неравенство (10.1.5) порождает решающее правило:

если , то решение «Н₁»;

если , то решение «Н₀».

Критическая поверхность и критическая область. Поскольку в данной задаче существует достаточная статистика и, соответственно, найдено пороговое решающее правило, для дальнейшего решения задачи форма и положение критической области не нужны. Однако, этот вопрос полезно прояснить для лучшего понимания задачи и, вообще, характера испытания простых гипотез. Из вида решающего правила (10.1.5) при m₀<m₁ и выражения (10.1.2) видно, что критическая поверхность представляет собой гиперплоскость в n-мерном выборочном пространстве W. Из вида выражения (10.1.6) для порога видно, что эта плоскость перпендикулярна прямой, соединяющей точки математических ожиданий в гипотезах Н₀, Н₁ , т. е. точки m₀=(m₀, m₀,..., m₀) и m₁=(m₁, m₁,..., m₁). Полученное ниже выражение для порога показывает, что от фиксированного значения форма и ориентация критической поверхности не зависит; при изменении критическая поверхность остается гиперплоскостью, перпендикулярной указанной прямой, меняется только точка пересечения плоскости и прямой: она находится между m₀ и m₁ , и с увеличением придвигается ближе к m₀ . Критическая область w занимает ту часть пространства W, которая находится по одну сторону от критической плоскости, а именно, на стороне точки m₀.

Вычисление порога. Мы получили пороговое решающее правило, однако порог пока не определен. Его следует определять по фиксированному значению (см. п. 9.3). Поскольку решающее правило отвергает Н₀ при совершении события , то условная вероятность этого события

.

Вероятность в левой части равенства легко найти: поскольку в гипотезе Н₀ распределение каждого выборочного значения есть N(m₀, 1), то m* имеет распределение (см. п. 5.3) N(m₀, ) c плотностью

.

Теперь

.

(10.1.7)

Интеграл в правой части не выражается конечной комбинацией элементарных функций, выразим его через специальную функцию «интеграл вероятности» (см. п. 3.8):

,

(10.1.8)

Сделав в интеграле (10.1.7) замену переменной

,

получаем его в виде

,

и сравнивая его с (10.1.8), получаем (10.1.7) в виде

.

(10.1.9)

Учитывая свойство

,

(10.1.10)

запишем (10.1.9) проще:

,

(10.1.11)

и вводя обозначение

,

(10.1.12)

находим

.

(10.1.13)

Учитывая, что выражается через порог , видим, что нашли выражение фиксируемой вероятности ложной тревоги через порог; но нам нужно обратное выражение порога через . Чтобы его получить, введем функцию (.), обратную функции (.), тогда из (10.1.13) находим

.

(10.1.14)

Окончательно, выражая из (10.1.12) и подставляя (10.1.14), получаем

.

(10.1.15)

Порог найден, (10.1.15) позволяет вычислить его по заданному . Для этого используются таблицы функции (.), или таблицы функции (.), или любой компьютерный статистический пакет. Пусть, например, m₀=2, n=25, зафиксируем на уровне =0.05. С помощью таблиц функции (.) находим (0.05)=-1.6449, и из (10.1.15) получаем порог

.

Вычисление мощности критерия. В этой задаче мощность критерия (см. п. 9.1) можно выразить через параметры задачи и порог в явном виде, что бывает не всегда. Из (9.1.5)

,

(10.1.16)

однако вычисление таким способом очень сложно. Согласно полученному решающему правилу, гипотеза Н₁ принимается тогда, когда совершается событие . Мощность критерия как условная вероятность принятия Н₁ при условии, что на самом деле справедлива Н₁ , равна

.

Сравнивая это выражение с (10.1.7), видим, что можем сразу получить , если в выражении для заменить m₀ на m₁ . Поэтому, сделав эту замену в (10.1.11), сразу находим

.

(10.1.17)

Зададим вопрос: как зависит мощность критерия от параметров задачи m₀, m₁, n? «Различие» между гипотезами Н₀ и Н₁ возрастает с увеличением разности m₁-m₀ , а «информативность» выборки возрастает с увеличением n, поэтому интуитивно ясно, что мощность критерия будет монотонно расти с увеличением как разности m₁-m₀ , так и величины n. Учитывая монотонно возрастающий характер функций и формулы (10.1.15), (10.1.16), можно легко убедиться, что это предположение верно.

Сформулируем теперь конкретный алгоритм испытания двух простых нормальных гипотез.

1) Задаем критическое значение .

2) По формуле (10.1.15) находим порог .

3) По формуле (10.1.2) находим статистическое среднее m*, играющее в данном случае роль решающей статистики в пороговом решающем правиле.

4) Сравнивая m* с порогом, принимаем решение «Н₁» или «Н₀».

5) По формуле (10.1.17) находим мощность критерия .

6) Находим вероятность пропуска как .

10.2. Испытание гипотез с распределениями Коши.

В задаче об испытании простых нормальных гипотез критическая поверхность имела одну и туже форму и ориентацию при любом фиксированном , менялось только ее положение. То же относилось к форме критической области. В общем случае это не так, что показывает рассматриваемая в этом пункте задача.

Рассмотрим испытание простых гипотез

H₀: ,

Н₁: ,

т. е. генеральная величина распределена в гипотезе Н₀ по закону Коши с параметром = 0, а в гипотезе Н₁ - по закону Коши с параметром = 1. Обычно n>>1, но в данном случае, для простоты теоретического рассмотрения, примем n=1.

Отношение правдоподобия

J(x)=f(x/H₀)/f(x/H₁)=[1+(x-1)²]/[1+x²].

Неравенство для критической области

[1+(x-1)²]/[1+x²] ,

где - порог. Собирая члены с одинаковыми степенями х, приведем это неравенство к виду

x²(-1)+2x+(-2)0.

Мы видим, что сам вид критической области w зависит от . Например, если =1, то неравенство принимает вид 2х1, т. е. х1/2 и критическая область - бесконечный полуинтервал w: x; а если =1/2, то неравенство принимает вид x²-4x+30, и критическая область - конечный интервал w: x[1, 3].

При n=1 в этой задаче, так же как в предыдущей, имеется достаточная статистика: это само выборочное значение х, его можно использовать как решающую статистику вместо J. Дальнейшие действия проведем только для названных частных случаев.

А) =1. Фиксированное значение равно

,

мощность критерия

.

Б) =1/2.

,

.

10.3. Испытание нормальной гипотезы

против гипотезы с распределением Лапласа.

До сих пор гипотезы Н₀ , Н₁ предполагали распределения одинакового вида, но с разными параметрами. Лемма Неймана-Пирсона справедлива в любом случае двух простых гипотез, в том числе и таком, когда вид распределения в гипотезах разный.

Рассмотрим испытание двух простых гипотез

Н₀: (N(0, 1)),

Н₁: , ,

т. е. генеральная СВ распределена в гипотезе Н₀ по каноническому нормальному закону, а в гипотезе Н₁ - по закону Лапласа с единичной дисперсией. Заметим, кстати, что в обоих случаях m_x=0 и =1. Опять для простоты математических выкладок рассматриваем случай n=1. Отношение правдоподобия

J(x)=f(x/H₀)/f(x/H₁)=;

неравенство для критической области

J(x)

после логарифмирования приводится к виду

,

и критическая область имеет вид

Решающее правило:

если xw, то решение «Н₁»,

если хw, то решение «Н₀».
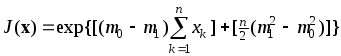
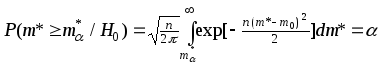