ТОПИН.Лекции, задания / ТОППиН_часть1 / глава 4_

109

Наиболее просто, как указано выше, математический анализ работы СМО выполняется в случае марковского процесса.

Для анализа используется граф переходов и уравнения Колмогорова. В частности, имеет место граф переходов, который носит название «схема гибели и размножения» (рис. 4.11), которая ведет свое начало от биологических задач.

Рисунок 4.11.

Состояния системы пронумерованы по числу требований, находящихся в системе. Это число совпадает с числом занятых каналов, если в системе п каналов.

0 – в СМО нет ни одного требования, 1 – в СМО находится одно требование (занят один канал, остальные

свободны),

- - - - - - - - - - - - - -

k – в СМО находится k требований (k каналов заняты, остальные свободны),

- - - - - - - - - - - - - -

п – в СМО находится п требований (все п каналов заняты).

Обратные переходы происходят следующим образом. Полагаем, что интенсивности обслуживания μ всех каналов одинаковы. Тогда, чтобы произошел переход системы из состояния 1 в состояние 0, необходимо, чтобы первый канал обслужил требование с интенсивностью μ, т.е. μ10 = μ. Если система находится в состоянии 2 (работают два канала), то для перехода в состояние 1, необходимо, чтобы закончил обслуживание либо первый канал, либо второй. Суммарная интенсивность их потоков обслуживания равна 2μ, т.е. μ21 = 2μ. Суммарный поток обслуживания k каналами

имеет интенсивность k μ, т.е. μk, k-1 = k μ и т.д.

Как правило полагают, что все потоки событий переводящие СМО из состояния в состояние простейшие.

При стационарном (устойчивом) процессе система уравнений Колмогорова записывается следующим образом:

и т.д.

n

Нормировочное условие Pi 1.

i 0

110

Из 1-го уравнения находим

P01 P .

110 0

Из 2-го:

Для k-го состояния:

и т.д.

Подставим все Рi в нормировочное условие:

Откуда вероятность 0-го состояния будет равна

Следовательно, Р0 есть величина, обратная сумме всех коэффициентов в вероятностях Pi , i 0, n .

Если интенсивности обслуживания всех каналов одинаковы, то знаменатели коэффициентов перед Р0 будут:

Введем понятие коэффициента загрузки ρ (или приведенная интен-

сивность потока требований, или коэффициент использования СМО):

.

Тогда (обозначая ρ по индексу μ):

Pk k Pk 1 k k 1 2 1 P0 ,

P0 1 1 2 1 n n 1 2 1 1.

Величина ρ (по смыслу) – это среднее число требований, приходящее за среднее время обслуживания одного требования.

Рассмотрим два типа СМО.

111

4.6.1. Многоканальная СМО с отказами [38]

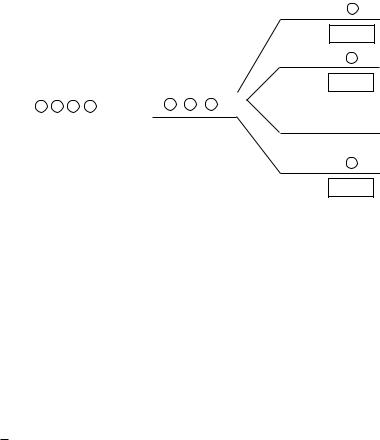
Если рассматривать п-канальную СМО (рис. 4.12) с отказами, то ее граф представлен на рис. 4.11.

Задача ставится так: имеется п-каналов, на которые поступает поток требований на обслуживание с интенсивностью λ. Поток обслуживания имеет интенсивность μ (величина, обратная среднему времени обслуживания Тобсл ср). Финальные вероятности состояний СМО найдены выше:

Р0, Р1, Р2, …, Рk, …. .

Узел обслуживания (приборы)

Входной

поток требований Накопитель

Рисунок 4.12.

По финальным вероятностям необходимо найти характеристики эффективности СМО:

Nср аб – абсолютную пропускную способность, т.е. среднее число требований, обслуживаемых в единицу времени;

Робсл – относительную пропускную способность, т.е. среднюю долю пришедших требований, обслуживаемых системой;

Ротк – вероятность отказа, т.е. того, что требование покинет СМО необслуженным;

k – среднее число занятых каналов.

Определим Ротк – вероятность того, что пришедшее требование получит отказ (не будет обслужено). Для этого нужно, чтобы все п каналов были заняты

Находим относительную пропускную способность – вероятность того, что требование будет обслужено:

Робсл = 1 – Ротк .

Абсолютная пропускная способность получится умножением интенсивности потока требований λ на Робсл:

Nср аб = λ Робсл.

112

Каждый занятый канал в единицу времени обслуживает в среднем μ требований. Следовательно, среднее число занятых каналов равно

k Ncp аб .

Обозначим через tож среднее время ожидания очереди одной заяв-

кой.

За время Т в систему придет λТ требований. Их среднее время ожидания равно λТ tож . Среднее число требований в очереди равно [39]:

Среднее число требований в системе (на приборах и в накопителе)

Nср аб = λ Тср,

где Тср – среднее время пребывания в системе. Отсюда

T Ncp аб .

cp

4.6.2. Одноканальная СМО с неограниченной очередью [38]

В этом случае на очередь не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На СМО поступает поток требований с интенсивностью λ, поток обслуживания имеет интенсивность μ.

Граф переходов приведен на рис. 4.13 (схема гибели и размножения с бесконечным числом состояний).

Рисунок 4.13.

Состояния системы: 0 – канал свободен;

1 – канал занят (обслуживает требование, очереди нет); 2 – канал занят, одно требование стоит в очереди;

- - - - - - - - - - - - - - - - - - -

k – занят канал, k – 1 требования стоят в очереди.

Поток требований с интенсивностью λ переводит систему слева направо, а поток обслуживаний с интенсивностью μ переводит систему справа налево.

113

Для такой системы нет надобности вычислять абсолютную Nср аб и относительную Робсл пропускные способности, т.к. очередь неограниченна и каждая заявка рано или позже будет обслужена. Поэтому Nср аб =λ и Робсл = 1.

Характеристиками эффективности такой системы будут: Nср, Тср,

Nоч , tож , Рзан:

Nср – среднее число требований в системе;

Тср – среднее время пребывания требования в системе; Nоч – среднее число требований в очереди;

tож – среднее время ожидания требования в очереди;

Рзан – вероятность того, что канал занят.

Финальные вероятности такой системы будут существовать только при ρ < 1.

Ряд в формуле представляет собой геометрическую прогрессию. Число слагаемых в этой формуле бесконечно. При ρ < 1 ряд сходится – бесконечно убывающая геометрическая прогрессия. При ρ > 1 ряд расходится.

Суммируя прогрессию, получим

Тогда Р0 = 1 – ρ.

Вероятности Р1, Р2, …, Рk, … находятся по формулам:

Среднее число требований в системе

Среднее время пребывания требования в системе

Среднее число требований в очереди

Среднее время ожидания требования в очереди

Вероятность того, что канал занят равно единице минус вероятность того, что канал свободен

114

Рзан = 1 – Р0 = ρ.

Среднее время обслуживания

4.7. Оптимизация. Методы оптимизации

4.7.1. Общие сведения. Терминология

Некоторые сведения об оптимизации, которые необходимо учитывать при изучении данного раздела, даны в § 1.13.

Проблема оптимальности является одной из важнейших в области конструирования и производства ЭА, так как решение этой проблемы позволяет повышать эффективность изделий и технологических процессов. Принятие тех или иных решений также не обходится без применения методов оптимизации.

Оптимизация (от лат. Optinum – наилучшее) – это процесс нахождения экстремума функции или выбор наилучшего (оптимального) варианта из множества возможных вариантов (альтернатив).

Какую бы техническую задачу ни решал конструктор или технолог, он всегда стремится получить наилучший или оптимальный ответ. Любая практически реализованная конструкция или любой технологический процесс могут рассматриваться с определенной точки зрения как оптимальные, так как имелись определенные основания для предпочтения их остальным. Однако в принципе выбор оптимального варианта является сложной и трудоемкой задачей, не решенной полностью до сих пор.

Если рассматривать задачи оптимизации в конструировании и технологии, то их можно сформулировать следующим образом.

Задача оптимизации в конструировании состоит в выборе наилучшего в некотором определенном смысле варианта технического решения из большого числа возможных вариантов.

Задача оптимизации в технологии состоит в том, чтобы наилучшим образом построить технологический процесс и определить оптимальные режимы его проведения.

При разработке конструкций ЭА и технологических процессов ее производства решается большое количество задач, из которых вытекает многообразие задач оптимизации.

Так при конструировании ЭА решаются задачи:

оптимизация параметров;

оптимизация структур по критериям минимальных массы, затрат, габаритам, числу внутренних и внешних связей, суммарной длине соединительных проводников, числу пересечений соединительных проводников, магнитным и электрическим взаимодействиям;

115

оптимизация конструкции модулей различных уровней по надежности, тепловому режиму, по размещению, по технологичности, по стоимости;

оптимальное резервирование с учетом ограничений по массе, габаритам, стоимости;

оптимизация требований к надежности элементов;

оптимизация количества запасных элементов;

оптимизация последовательности проверок ЭА при ограниченном времени восстановления и другие.

При разработке производственных процессов изготовления ЭА решаются задачи:

оптимизация структуры производственного процесса и его отдельных звеньев;

оптимизация использования при производстве данного изделия технологических процессов и производств;

оптимизация затрат труда, средств и времени на изготовление изделия;

оптимизация номенклатуры технологических документов, применяемых в качестве директивных;

оптимизация типовых, групповых и пр. технологических процессов;

оптимизация раскроя материалов и другие.

Прежде чем приступить к изучению математических методов оптимизации, необходимо ознакомиться с рядом понятий.

Объект оптимизации – система или изделие, подвергаемые оптимизации.

Факторное пространство – это пространство (область) Х с координатами xi , i 1,n , которые соответствуют независимым переменным си-

стемы, варьируемым при исследовании.

Функция отклика F (целевая функция) – функция, связывающая параметр оптимизации y с переменными, варьируемыми при исследовании

y = F(x1, x2, …, xn).

Поверхность отклика – геометрическое изображение функции отклика в факторном пространстве.

При изложении вопросов, связанных с поиском экстремума, полезно использовать графическое изображение поверхности отклика и траектории движения от исходной точки к экстремальной в пространстве управляемых параметров, получающейся в результате ряда последовательных шагов поиска.

Поверхность отклика функции изображают в виде совокупности линий равного уровня. Линия равного уровня – множество точек пространства, в которых рассматриваемая функция имеет одинаковые значения,

116

равные заданной величине (при двух переменных x1 и x2). При трех переменных линии равного уровня становятся поверхностными, а при п > 3 – гиперповерхностными равного уровня (рис. 4.14)

Изображающая точка – точка в факторном пространстве, характеризующая состояние системы (в рассматриваемый момент времени).

Глобальный экстремум – это наибольшее (наименьшее) значение функции отклика F(x1,…, xn) в пределах всей области Х переменных xi (точка 01 на рис. 4.14).

Локальный экстремум – это наибольшее (наименьшее) значение

функции отклика F(x , …, x ) в некоторой точке по сравнению с ее

1 n a X

значениями в точках, принадлежащих малой окрестности точки a (точка

02 на рис. 4.14).

Если в пределах области Х имеется всего один экстремум, то он обязательно будет глобальным.

Рисунок 4.14.

Экстремум называется граничным, если он имеет место в граничных точках области Х, и внутренним, если он соответствует внутренней точке области Х.

Экстремум называется безусловным, если на переменные xi не накладывается никаких ограничений, и условным, если переменные xi связаны ограничениями типа равенств.

При оптимизации могут решаться задачи:

–задача классической оптимизации;

–задача неклассической оптимизации.

Классическая задача оптимизации заключается в оптимизации целевой функции

y = F(x1, x2, …, xn) = extr,

117

т.е. определяются такие значения независимых переменных (проектных параметров) xi, при которых целевая функция приобретает экстремальное значение с учетом всякого рода ограничений.

Неклассическая задача оптимизации имеет место, когда неизвестна функциональная зависимость между показателем качества (параметром оптимизации) y и параметрами xi. Поэтому в такой задаче оптимизируется не только целевая функция, но и сам способ оптимизации. Другими словами при неклассической задаче оптимизации выбирают также оптимальную стратегию поиска экстремума, а не только оптимальное значение параметра оптимизации y.

В общей структуре проектирования и изготовления электронной аппаратуры можно выделить три этапа оптимизации:

–структурная оптимизация – выбор наилучшей конструкторской реализации ЭА, обеспечивающей выполнение заданных функциональных требований;

–параметрическая оптимизация – выбор наилучшего соотноше-

ния номинальных параметров, обеспечивающих заданные электрические характеристики, и определение допусков на параметры элементов по допустимому отклонению выходных параметров;

–технологическая оптимизация – выбор номинальных значений конструкционных параметров и технологической точности на них, исходя из производственных и экономических требований.

На каждом из этапов встает проблема формулировки критерия оптимальности и оптимального решения задачи. Однако системный подход подразумевает общую оптимизацию проектирования и изготовления ЭА, так что в отдельности каждое из них может и не быть оптимальным.

Общая форма показателя оптимальности (эффективности функционирования) должна вытекать из основного постулата исследования операций: оптимальным решением является то решение, которое обеспечивает выполнение поставленной задачи при минимуме материальных затрат, либо то, которое обеспечивает выполнение поставленной задачи с максимальной эффективностью при фиксированных материальных затратах [44*].

4.7.2. Постановка и содержание задачи оптимизации

Задача оптимизации ставится следующим образом. Имеется целевая функция (показатель качества, показатель эффективности функционирования, параметр оптимизации)

y F(x1, x2 ,...,xn ) F(x), i 1,n

и функциональные ограничения типа равенств, неравенств и дискретности, которые накладываются на значения каждого из проектных параметров в отдельности и на связи между ними. Например, функции ограничений или функции связи могут иметь вид