ТОПИН.Лекции, задания / ТОППиН_часть1 / глава 4_

89

Глава 4 МАТЕМАТИЧЕСКИЙ АППАРАТ БОЛЬШОЙ СИСТЕМЫ

4.1. Общие сведения

Математический аппарат, используемый в рассматриваемой большой системе очень разнообразен из-за разнообразия функций и процессов, имеющих место в подсистемах.

Теория множеств и теория графов используются при проектировании конструкций аппаратуры.

Теория подобия и моделирования используется для создания моделей и исследования разрабатываемых конструкций и технологических процессов.

Теория вероятностей и математическая статистика широко используются при построении математических моделей из-за множества случайных воздействий при производстве и эксплуатации.

Методы пассивного и активного экспериментов применяются для построения математических моделей процессов.

Методы оптимизации позволяют отрабатывать на моделях качество объектов и технологических процессов при тех или иных ограничениях.

Теория случайных процессов дает возможность описания и исследования самых разнообразных процессов, происходящих в конструкциях аппаратуры при производстве и в эксплуатации.

Теория массового обслуживания позволяет решать многочисленные задачи обслуживания объектов при производстве и эксплуатации.

Теория надежности используется для исследования объектов и повышения надежности на всех этапах их «жизни».

Как отмечается в [35], все многообразие разработанных и используемых для исследования сложных стохастических процессов математических методов можно разбить на две группы:

вероятностно-статистические методы, включающие использование общих идей теории вероятностей, выборочного метода и проверку статистических гипотез, дисперсионного и регрессионного анализов, статистического планирования эксперимента;

методы исследования операций, включающие линейное, нелиней-

ное и динамическое программирование, теорию массового обслуживания, теорию игр, теорию графов и сетей.

Первые методы успешно применяются для решения технологических задач:

статистический анализ накопленных данных о техпроцессах и свойствах изделий для обобщения информации, для изучения влияния производственных факторов на показатели изделий;

90

разработка математико-статистических моделей для принятия оптимальных технических и экономических решений, а также для

управления процессом или отдельными операциями с использованием ЭВМ.

Общая схема решения технологических задач математикостатистическими методами приведена на рис. 4.1 [35].

Рисунок 4.1.

Вторые методы применяются для решения задач проектирования и обслуживания.

Если говорить о моделях, то существуют аналитические и статистические модели. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато

91

результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А главное, аналитические модели более приспособлены для поиска оптимальных решений.

Статистические модели, по сравнению с аналитическими, более точны и подробны, не требуют грубых допущений, позволяют учесть большое число факторов. Но их недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходится искать «на ощупь», путем догадок и проб.

Поскольку некоторые из перечисленных математических методов, необходимых для принятия того или иного решения, составляют науку «Исследование операций», приведем некоторые сведения о ней.

4.2. Исследование операций

Исследование операций – это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (или оптимального) управления в различных областях целенаправленной человеческой деятельности.

Операция – это совокупность взаимосогласованных действий, направленных на достижение вполне определенных целей.

Цель исследования операций – количественные обоснование принимаемых решений по управлению.

Основная задача исследования операций – нахождение в рамках принятой модели таких решений, которые обеспечивают экстремальное значение показателя эффективности.

Задачи исследования операций (ИО) можно разделить на две большие группы [36]:

1.Тактические задачи – задачи выбора оптимальных методов использования технических устройств.

2.Технические задачи – задачи выбора оптимальных характеристик технических устройств.

Рассмотрим содержание технических задач, имея в виду цели иссле-

дования.

Первая техническая задача ИО – задача определения целесообразности сроков разработки новых технических устройств. Решение этой задачи должно помочь ответить на первый вопрос, возникающий при начале проектирования нового технического устройства – стоит ли вообще начинать разработку нового технического устройства, может целесообразнее воспользоваться уже разработанными техническими устройствами.

Вторая техническая задача ИО – задача выбора оптимального ряда (типажа) технических устройств, т.е. их оптимальных характеристик. Эта задача решается с применением рядов предпочтительных чисел, которые должны быть положены в основу выбора градаций параметров и размеров [37].

92

Третья техническая задача ИО – задача выбора оптимального сочетания проектных параметров.

Четвертая техническая задача ИО – выбор лучшего из «конкурирующих» технических устройств.

Все задачи ИО (тактические и технические) по содержанию принято делить на следующие типы:

1.Распределительные задачи (распределение ресурсов наилучшим образом).

2.Задачи управления запасами. Например, задача выбора оптимального ЗИП (Запасной Инструмент и Принадлежности).

3.Задачи замены оборудования. Например, задачи определения оптимальных сроков разработки новых видов технических устройств, оптимальных сроков профилактической замены элементов, деталей, узлов.

4.Задачи массового обслуживания.

5.Состязательные задачи. Например, задачи об оптимальных стратегиях (т.е. методах действия) двух сторон. Используется теория игр.

6.Задачи упорядочения. Например, задачи сетевого планирования.

7.Задачи поиска. Например, отыскание какого-либо объекта, неисправного элемента и т.п.

8.Задачи выбора оптимальных режимов движения (задача коммивояжера).

Три методологических особенности ИО:

системный подход к анализу поставленной задачи: частная задача влияет на общую, часть системы на всю систему;

оптимальное решение поставленной задачи;

комплектность операционных исследований, т.е. по многим направлениям. Создаются комплексные группы, в которые входят инженеры, математики, экономисты, социологи, психологи и т.д.

Основные этапы операционного исследования:

1.Содержательная постановка задачи (она обычно не бывает окончательной и постепенно уточняется); на этом этапе выполняется формулировка критерия и формирование показателя оптимизации;

2.Построение математической модели – формализация задачи;

3.Нахождение метода оптимального решения задачи. Используются методы математического программирования;

4.Проверка и корректировка модели;

5.Реализация найденного решения на практике.

Исследование операций широко использует математические методы

– теорию вероятностей, математическую статистику, теорию массового обслуживания, теорию игр, методы оптимизации, метод статистических испытаний и т.п.

При исследовании операций (нахождении показателей управляемых параметров, максимизирующих целевую функцию) следует учитывать ограничения, накладываемые на управляемые параметры, выходные параметры, условия проведения операций и т.п.

93

Считается, что математическая модель построена, если имеются следующие зависимости для выходных параметров yi (частные целевые функции) и обобщенной целевой функции W:

yi Fi x1, x2 ,...,xn ; f1, f2 ,..., fs , i 1, m,

WW y1, y2 ,...,ym

изависимости, выражающие ограничения

где xr , r 1, n – управляемые параметры,

f p , p 1, s – неуправляемые параметры, определяющие условия, в ко-

торых проводится операция.

Задача исследования операции состоит в том, чтобы из множества допустимых решений выбрать оптимальные, т.е. определить значения управляемых параметров х1, х2, …, хn, удовлетворяющих заданным ограни-

чениям j , j 1,l и обращающих в максимум (минимум) целевую функцию W.

4.3. Случайные функции и процессы

Параметры элементов и систем в связи с влиянием на них большого количества факторов на этапах проектирования, производства и эксплуатации, имеют случайный характер. Если рассматривать эти параметры при конкретных значениях факторов, от которых они зависят, то параметры будут представлять собой случайные величины. Наилучшим описанием случайной величины является закон ее распределения, приближенным – числовые характеристики (моменты) распределения. Однако представление параметров элементов и систем как случайных величин допустимо лишь в первом приближении.

Для более полного представления о функционировании изделий в реальных условиях эксплуатации необходимо знать, как изменяются их параметры при изменении влияющих факторов. Такое представление дают случайные функции и процессы.

Случайная функция – это функция, которая в результате опыта может принять тот или иной конкретный вид, но неизвестно заранее какой именно. Конкретный вид, принимаемый случайной функцией в результате однократного опыта, называется реализацией случайной функции (рис. 4.2), где: y – параметр, x – фактор.

Случайная функция y(x) = f(x). Конкретные значения y при заданных значениях x являются случайными величинами: y1 = y(x = x1), y2 = y(x = x2).

95

Математическое ожидание M[y(x)] случайной функции y(x) есть неслучайная функция my(x), которая при каждом значении аргумента x равна математическому ожиданию (МО) соответствующего сечения случайной функции

[ y(x)] my (x) y f ( y, x) dy,

где f(y, x) – одномерная плотность вероятностей семейства реализаций случайных функций.

По смыслу МО случайной функции есть некоторая средняя функция, около которой группируются и относительно которой колеблются все реализации случайных функций.

Дисперсия случайной функции y(x) есть неслучайная функция Dy(x), значение которой для каждого x равно дисперсии соответствующего сечения случайной функции

Дисперсия Dy(x) характеризует разброс реализаций в семействе относительно МО my(x).

Среднеквадратичное отклонение случайной функции

y (x) Dy (x).

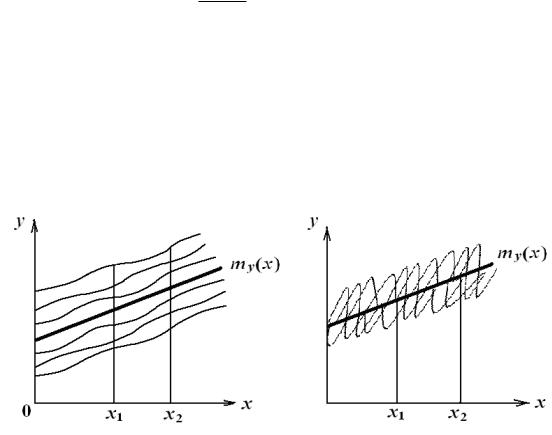
Одномерная плотность распределения f(y, x) позволяет найти среднее значение случайной функции и ее дисперсию, но не содержит информации о поведении случайной функции. Например, две случайные функции обладают одинаковыми средними значениями, но одна из них представляет плавно меняющиеся случайные функции, а другая сильно перемешанные. У первой из них сильно связанные значения y для сечений x1 и x2 (рис. 4.4а), у другой эти значения независимы (рис. 4.4б).

96

Вводится двумерная плотность распределения случайной функции, которая показывает насколько связаны между собой значения случайной функции при двух различных значениях аргумента. Для количественной оценки этой связи (изменения случайной функции с изменением аргумента x) используется автокорреляционная функция (АКФ).

АКФ семейства реализаций случайной функции называется детерминированная функция двух аргументов, которая при каждой паре значений аргумента x1 и x2 равна корреляционному моменту соответствующих значений семейства реализаций случайной функции.

K y (x1 , x2 ) y(x1 ) my (x1 ) y(x2 ) my (x2 )

f y(x1 ), x1; y(x2 ), x2 dyx1 dyx2 .

Функция f [ y(x1 ), x1; y(x2 ), x2 ] в данном случае представляет собой

двумерную плотность вероятностей y(x).

АКФ содержит данные из двух сечений семейства реализаций случайной функции. Следовательно, она определяется двумерными свойствами семейства реализаций. Назначение АКФ – характеризовать степень зависимости между сечениями случайной функции, относящимся к различным значениям аргумента х.

Взаимосвязь вероятностных свойств двух случайных функций y(x1) и z(x2) обычно характеризуется взаимной корреляционной функцией (ВКФ).

B(x1 , x2 ) y(x1 ) my (x1 ) z(x2 ) mz (x2 )

f y(x1 ), x1; z(x2 ), x2 dyx1 dzx2 ,

где f y(x1 ), x1; z(x2 ), x2 – совместная плотность вероятностей значений

y(x1) и z(x2).

Случайный процесс есть случайная функция от независимой переменной t-времени: y(t).

Следовательно, если в качестве аргумента используется время, то имеем дело со случайными процессами.

Реализации случайного процесса называются траекториями. Все что говорилось о случайных функциях полностью относится к случайным процессам с аргументом t. Характеристики случайных процессов анало-

гичны характеристикам случайных функций: МО, D, σ, АКФ, ВКФ случайных процессов.

В качестве дополнительной характеристики для стационарных случайных процессов (процессов, которые протекают во времени приблизительно однородно) используют интервал корреляции

k Ry ( ) d ,

0

где Ry(τ) – нормированная АКФ процесса.

97

Это позволяет более просто, хотя и более грубо, описать быстротечность процесса.

Величина τk дает ориентировочное представление о том, на каких интервалах времени в среднем имеет место существенная корреляция между значениями случайного процесса. Максимальный интервал корреляции – такой интервал, за пределами которого корреляция между

значениями случайного процесса пренебрежимо мала, т.е. Ry k м акс ,

где α= 0,1,…, 0,01 – некоторая малая, наперед заданная величина.

В теории случайных процессов принято классифицировать их по тем или другим признакам, учитывая плавность или скачкообразность реализации, фиксированность или случайность моментов, в которые могут происходить скачки и т.д., вид закона распределения отдельного сечения процесса или совокупности его сечений и т.д. Самая элементарная классификация случайных процессов – «по времени» и «по состояниям».

Случайный процесс с дискретным временем – это процесс в системе, которая может менять свои состояния только в отдельные моменты време-

ни t1, t2 и т.д.

Случайный процесс с непрерывным временем – если переходы из одного состояния в другое могут происходить в любой момент времени.

Случайный процесс с непрерывными состояниями, если его сечение в любой момент времени представляет собой непрерывную случайную величину и, значит, множество ее значений несчетно.

Случайный процесс с дискретными состояниями, если в любой момент времени множество его состояний конечно или счетно, т.е. случайная величина в сечении дискретна.

В соответствии с вышеизложенным приведем одну из классификаций случайных процессов (четыре класса):

I. Параметр t дискретен и множество состояний дискретно. II. Параметр t непрерывен, множество состояний дискретно. III. Параметр t дискретен, множество состояний непрерывно.

IV. Параметр t непрерывен и множество состояний непрерывно.

К I типу можно отнести дискретные цепи Маркова, последовательности дискретных случайных величин. К II типу – Марковские цепи с непрерывным множеством состояний. Тип III представляет процесс Пуассона. В IV тип входит броуновское движение, сюда же относятся случайные процессы общего типа.

На рисунке 4.5 представлены диаграммы:

а) дискретной случайной последовательности (х и t – дискретны);

б) дискретного случайного процесса (х – дискретно, t – непрерывно); в) непрерывной случайной последовательности (х – непрерывно, t –

дискретно);

г) непрерывного случайного процесса (х и t – непрерывны).

98

а) xk

t

в) х

г) х

tk

Рисунок 4.5.

Все процессы можно также классифицировать и из других соображений, например:

1.Стационарные – нестационарные;

2.Гауссовские – негауссовские;

3.Марковские – немарковские

ит.д.

Некоторые из случайных процессов (стационарный, Марковский и др.) широко используются в теории надежности, так как позволяют с достаточной точностью описать процессы, происходящие в элементах и системах.

4.4. Марковский случайный процесс

Основными математическими методами анализа функционирования систем являются марковские процессы.