4.6.1. Многоканальная смо с отказами [38]

Если рассматривать п-канальную СМО (рис. 4.12) с отказами, то ее граф представлен на рис. 4.11.

Задача ставится так: имеется п-каналов, на которые поступает поток требований на обслуживание с интенсивностью λ. Поток обслуживания имеет интенсивность μ (величина, обратная среднему времени обслуживания Т_{обсл ср}). Финальные вероятности состояний СМО найдены выше: Р₀, Р₁, Р₂, …, Р_k, …. .

Узел обслуживания (приборы)

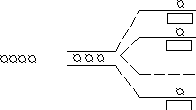
Входной

поток

требований Накопитель

Рисунок 4.12.

По финальным вероятностям необходимо найти характеристики эффективности СМО:

N_{ср аб} – абсолютную пропускную способность, т.е. среднее число требований, обслуживаемых в единицу времени;

Р_обсл – относительную пропускную способность, т.е. среднюю долю пришедших требований, обслуживаемых системой;

Р_отк – вероятность отказа, т.е. того, что требование покинет СМО необслуженным;

–среднее число занятых каналов.

Определим Р_отк – вероятность того, что пришедшее требование получит отказ (не будет обслужено). Для этого нужно, чтобы все п каналов были заняты

Р_отк

Находим относительную пропускную способность – вероятность того, что требование будет обслужено:

Р_обсл = 1 – Р_отк .

Абсолютная пропускная способность получится умножением интенсивности потока требований λ на Р_обсл:

N_{ср аб} = λ  Р_обсл.

Каждый занятый канал в единицу времени обслуживает в среднем μ требований. Следовательно, среднее число занятых каналов равно

Обозначим через среднее время ожидания очереди одной заявкой.

За время Т в систему придет λТ требований. Их среднее время ожидания равно λТ . Среднее число требований в очереди равно [39]:

Среднее число требований в системе (на приборах и в накопителе)

N_{ср аб} = λ  Т_ср,

где Т_ср – среднее время пребывания в системе.

Отсюда

4.6.2. Одноканальная смо с неограниченной очередью [38]

В этом случае на очередь не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На СМО поступает поток требований с интенсивностью λ, поток обслуживания имеет интенсивность μ.

Граф переходов приведен на рис. 4.13 (схема гибели и размножения с бесконечным числом состояний).

Рисунок 4.13.

Состояния системы:

0 – канал свободен;

1 – канал занят (обслуживает требование, очереди нет);

2 – канал занят, одно требование стоит в очереди;

- - - - - - - - - - - - - - - - - - -

k – занят канал, k – 1 требования стоят в очереди.

Поток требований с интенсивностью λ переводит систему слева направо, а поток обслуживаний с интенсивностью μ переводит систему справа налево.

Для такой системы нет надобности вычислять абсолютную N_{ср аб} и относительную Р_обсл пропускные способности, т.к. очередь неограниченна и каждая заявка рано или позже будет обслужена. Поэтому N_{ср аб} =λ и Р_обсл = 1.

Характеристиками эффективности такой системы будут: N_ср, Т_ср, ,,Р_зан:

N_ср – среднее число требований в системе;

Т_ср – среднее время пребывания требования в системе;

–среднее число требований в очереди;

–среднее время ожидания требования в очереди;

Р_зан – вероятность того, что канал занят.

Финальные вероятности такой системы будут существовать только при ρ < 1.

Ряд в формуле представляет собой геометрическую прогрессию. Число слагаемых в этой формуле бесконечно. При ρ < 1 ряд сходится – бесконечно убывающая геометрическая прогрессия. При ρ > 1 ряд расходится.

Суммируя прогрессию, получим

Тогда Р₀ = 1 – ρ.

Вероятности Р₁, Р₂, …, Р_k, … находятся по формулам:

Среднее число требований в системе

Среднее время пребывания требования в системе

Среднее число требований в очереди

Среднее время ожидания требования в очереди

Вероятность того, что канал занят равно единице минус вероятность того, что канал свободен

Р_зан = 1 – Р₀ = ρ.

Среднее время обслуживания