4.3. Случайные функции и процессы

Параметры элементов и систем в связи с влиянием на них большого количества факторов на этапах проектирования, производства и эксплуатации, имеют случайный характер. Если рассматривать эти параметры при конкретных значениях факторов, от которых они зависят, то параметры будут представлять собой случайные величины. Наилучшим описанием случайной величины является закон ее распределения, приближенным – числовые характеристики (моменты) распределения. Однако представление параметров элементов и систем как случайных величин допустимо лишь в первом приближении.

Для более полного представления о функционировании изделий в реальных условиях эксплуатации необходимо знать, как изменяются их параметры при изменении влияющих факторов. Такое представление дают случайные функции и процессы.

Случайная функция – это функция, которая в результате опыта может принять тот или иной конкретный вид, но неизвестно заранее какой именно. Конкретный вид, принимаемый случайной функцией в результате однократного опыта, называется реализацией случайной функции (рис. 4.2), где: y – параметр, x – фактор.

Случайная функция y(x) = f(x). Конкретные значения y при заданных значениях x являются случайными величинами: y₁ = y(x = x₁), y₂ = y(x = x₂).

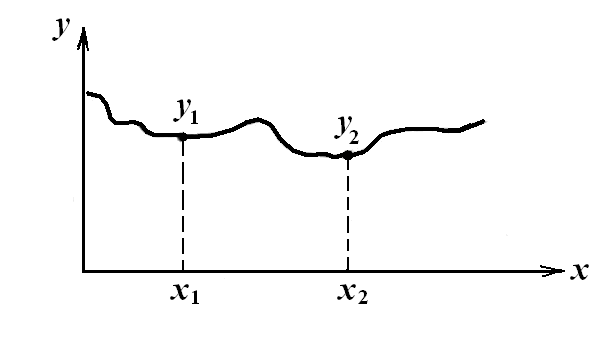
Рисунок 4.2.

Если над случайной функцией провести группу опытов, то получим семейство реализаций этой функции (рис. 4.3). Семейство реализаций случайной функции – основной экспериментальный материал, на основе которого можно получить характеристики случайной функции.

Рисунок 4.3.

Семейство реализаций можно рассматривать при разных значениях фактора x – в сечении семейства. В каждом сечении параметр y будет являться обычной случайной величиной, характеризуемой законом распределения, например, с плотностью

где m_y – математическое ожидание;

σ_y – среднеквадратическое отклонение.

Случайную функцию можно также определить как функцию своего аргумента, значение которой при любом значении ее аргумента является случайной величиной.

Характеристиками случайных функций, в отличие от числовых характеристик случайных величин, представляющих собой определенные числа, являются в общем случае не числа, а функции.

Математическое ожидание M[y(x)] случайной функции y(x) есть неслучайная функция m_y(x), которая при каждом значении аргумента x равна математическому ожиданию (МО) соответствующего сечения случайной функции

где f(y, x) – одномерная плотность вероятностей семейства реализаций

случайных функций.

По смыслу МО случайной функции есть некоторая средняя функция, около которой группируются и относительно которой колеблются все реализации случайных функций.

Дисперсия случайной функции y(x) есть неслучайная функция D_y(x), значение которой для каждого x равно дисперсии соответствующего сечения случайной функции

Дисперсия D_y(x) характеризует разброс реализаций в семействе относительно МО m_y(x).

Среднеквадратичное отклонение случайной функции

Одномерная плотность распределения f(y, x) позволяет найти среднее значение случайной функции и ее дисперсию, но не содержит информации о поведении случайной функции. Например, две случайные функции обладают одинаковыми средними значениями, но одна из них представляет плавно меняющиеся случайные функции, а другая сильно перемешанные. У первой из них сильно связанные значения y для сечений x₁ и x₂ (рис. 4.4а), у другой эти значения независимы (рис. 4.4б).

а) б)

Рисунок 4.4.

Вводится двумерная плотность распределения случайной функции, которая показывает насколько связаны между собой значения случайной функции при двух различных значениях аргумента. Для количественной оценки этой связи (изменения случайной функции с изменением аргумента x) используется автокорреляционная функция (АКФ).

АКФ семейства реализаций случайной функции называется детерминированная функция двух аргументов, которая при каждой паре значений аргумента x₁ и x₂ равна корреляционному моменту соответствующих значений семейства реализаций случайной функции.

Функция в данном случае представляет собой двумерную плотность вероятностей y(x).

АКФ содержит данные из двух сечений семейства реализаций случайной функции. Следовательно, она определяется двумерными свойствами семейства реализаций. Назначение АКФ – характеризовать степень зависимости между сечениями случайной функции, относящимся к различным значениям аргумента х.

Взаимосвязь вероятностных свойств двух случайных функций y(x₁) и z(x₂) обычно характеризуется взаимной корреляционной функцией (ВКФ).

где – совместная плотность вероятностей значений

y(x₁) и z(x₂).

Случайный процесс есть случайная функция от независимой переменной t-времени: y(t).

Следовательно, если в качестве аргумента используется время, то имеем дело со случайными процессами.

Реализации случайного процесса называются траекториями. Все что говорилось о случайных функциях полностью относится к случайным процессам с аргументом t. Характеристики случайных процессов аналогичны характеристикам случайных функций: МО, D, σ, АКФ, ВКФ случайных процессов.

В качестве дополнительной характеристики для стационарных случайных процессов (процессов, которые протекают во времени приблизительно однородно) используют интервал корреляции

где R_y(τ) – нормированная АКФ процесса.

Это позволяет более просто, хотя и более грубо, описать быстротечность процесса.

Величина τ_k дает ориентировочное представление о том, на каких интервалах времени в среднем имеет место существенная корреляция между значениями случайного процесса. Максимальный интервал корреляции τ_kмакс – такой интервал, за пределами которого корреляция между значениями случайного процесса пренебрежимо мала, т.е. , гдеα= 0,1,…, 0,01 – некоторая малая, наперед заданная величина.

В теории случайных процессов принято классифицировать их по тем или другим признакам, учитывая плавность или скачкообразность реализации, фиксированность или случайность моментов, в которые могут происходить скачки и т.д., вид закона распределения отдельного сечения процесса или совокупности его сечений и т.д. Самая элементарная классификация случайных процессов – «по времени» и «по состояниям».

Случайный процесс с дискретным временем – это процесс в системе, которая может менять свои состояния только в отдельные моменты времени t₁, t₂ и т.д.

Случайный процесс с непрерывным временем – если переходы из одного состояния в другое могут происходить в любой момент времени.

Случайный процесс с непрерывными состояниями, если его сечение в любой момент времени представляет собой непрерывную случайную величину и, значит, множество ее значений несчетно.

Случайный процесс с дискретными состояниями, если в любой момент времени множество его состояний конечно или счетно, т.е. случайная величина в сечении дискретна.

В соответствии с вышеизложенным приведем одну из классификаций случайных процессов (четыре класса):

I. Параметр t дискретен и множество состояний дискретно.

II. Параметр t непрерывен, множество состояний дискретно.

III. Параметр t дискретен, множество состояний непрерывно.

IV. Параметр t непрерывен и множество состояний непрерывно.

К I типу можно отнести дискретные цепи Маркова, последовательности дискретных случайных величин. К II типу – Марковские цепи с непрерывным множеством состояний. Тип III представляет процесс Пуассона. В IV тип входит броуновское движение, сюда же относятся случайные процессы общего типа.

На рисунке 4.5 представлены диаграммы:

а) дискретной случайной последовательности (х и t – дискретны);

б) дискретного случайного процесса (х – дискретно, t – непрерывно);

в) непрерывной случайной последовательности (х – непрерывно, t – дискретно);

г) непрерывного случайного процесса (х и t – непрерывны).

а)x_k

0 1 2 3 4 5 6 7

б) x_k

t

в) х

0 1 2 3 4 5 6 7 8

г) х

Рисунок 4.5.

Все процессы можно также классифицировать и из других соображений, например:

1. Стационарные – нестационарные;

2. Гауссовские – негауссовские;

3. Марковские – немарковские

и т.д.

Некоторые из случайных процессов (стационарный, Марковский и др.) широко используются в теории надежности, так как позволяют с достаточной точностью описать процессы, происходящие в элементах и системах.