4.7.3. Методы оптимизации

Классификаций методов оптимизации в литературе очень много. Одна из них представлена на рис. 4.15.

Термин «программирование» в названиях некоторых методов означает «планирование». Из рисунка следует, что существуют три группы методов:

аналитические,

алгоритмические (численные),

эвристические.

Аналитические методы используются, когда целевая функция, ограничения и связи между переменными и решениями, а также начальные и граничные условия представлены функциями, которые должны быть, по крайней мере, дважды дифференцируемы и иметь конечное число точек разрыва. Применение этих методов всегда предпочтительнее, поскольку они позволяют достаточно полно исследовать функцию и установить влияние различных факторов на эту функцию благодаря явному формульному решению задачи. Однако на практике применение этих методов ограничено большой математической сложностью и громоздкостью из-за сложности исходной математической модели. Они применяются для решения относительно простых задач.

Основное достоинство аналитических методов состоит в том, что они дают возможность качественной оценки результатов при изменении параметров. Численные же методы обеспечивают получение конкретных числовых значений параметров.

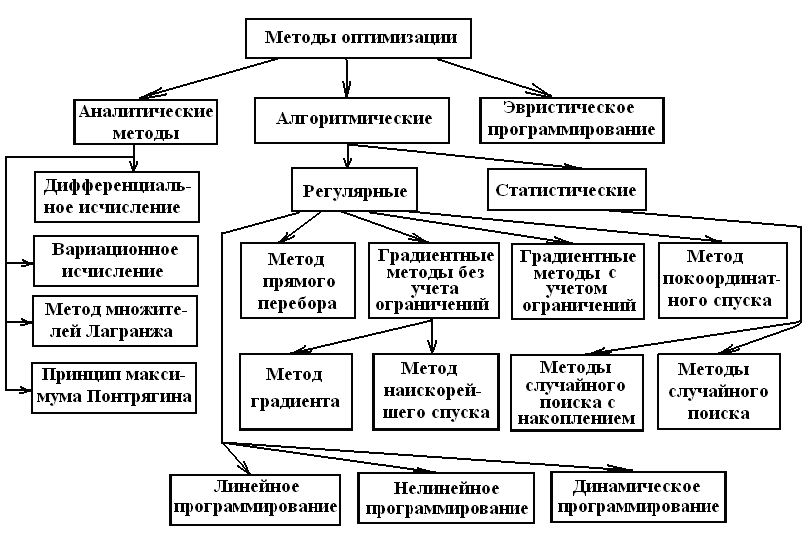
Рисунок 4.15.

Алгоритмические (численные) методы указывают пути отыскания положения экстремума. Так как можно указать различные способы отыскания экстремума, то имеется множество разновидностей алгоритмических методов оптимизации. Использование численных методов предполагает знание области возможных изменений решения, и чем эта область уже, т.е. чем больше ограничений, тем эффективнее применение численных методов оптимизации.

Эти методы находят применение при большом числе возможных переменных х₁, …, х_n и сложном виде целевой функции. Они применимы для решения любой задачи математической оптимизации, но являются весьма трудоемкими.

Вообще говоря, вид оптимизируемой функции и способ ее задания могут быть произвольными.

Основным недостатком численных методов является возможность получения не глобального, а локального экстремума исследуемой функции.

Принципиальное отличие численных методов от аналитических заключается в том, что процесс нахождения оптимального решения являетсямногошаговым, т.е. последовательное приближение к искомому решению. Это означает, что при поиске экстремальной точки осуществляется локальное изучение поверхности отклика по результатам ряда опытов, специально поставленных около исходной точки. Движение к экстремуму в многомерном пространстве независимых переменных осуществляется не непрерывно, а шагами. Анализируя результаты экспериментов и сравнивая их с результатами предыдущих, принимается решение о дальнейших действиях по поиску экстремума. Экстремальное значение функции отклика достигается с помощью многократного последовательного изучения поверхности отклика и продвижения в факторном пространстве. Фрагмент поверхности отклика приведен на рис. 4.16. Поверхность исследуется вокруг точек 0, 1, 2, между которыми делаются шаги.

К методу поиска экстремума предъявляются следующие требования:

1. траектория поиска должна заканчиваться в заданной -окрестности экстремальной точки, т.е. метод должен обеспечивать нахождение экстремума в заданной точностью;

2. затраты машинного времени на поиск экстремума при выполнении первого требования должны быть минимальными (минимальные потери на поиск).

Все алгоритмические методы оптимизации различаются способом определения направления движения и организацией самого движения.

В процессе оптимизации целевой функции , где<х₁, х₂, …, х_n >, вектору даются различные значения. В зависимости от того, как связаны последующие значения векторас предыдущими, алгоритмические методы делятся на методырегулярного и случайного поиска.

В регулярных методах выбор начального значения вектора однозначно определяет все его последующие значения. Большинство регулярных методов относится к числуградиентных. В их основе лежит вычисление градиента функции qrad, если она задана в явном виде. Если целевая функция задана в неявном виде, то градиент определяется путем «пробных шагов».

Градиентные методы делятся на два класса:

• градиентные методы без учета ограничений (градиентного спуска, наискорейшего спуска);

• градиентные методы с учетом ограничений (метод зигзагообразного движения, проекционный градиентный метод).

Из неградиентных регулярных методов наибольшее значение имеют:

• метод прямого перебора;

• метод покоординатного спуска (метод Гаусса-Зейделя).

Методы «спуска» служат для отыскания минимума функции, методы «подъема» служат для отыскания максимума функции. Процедуры поиска абсолютно одинаковы, меняется только знак.

Большой класс методов для решения задач оптимизации составляют методы математического программирования: линейного, нелинейного, целочисленного и динамического программирования.

Методы случайного поиска (статистические) принципиально отличаются от регулярных методов тем, что направление движения рабочей точки на каждом шаге не зависит от предыстории этого движения, а зависит от случайных причин. Эти методы используются для отыскания экстремума функции многих переменных при любых ограничениях. Использование специальных алгоритмов позволяет с некоторой вероятностью отыскивать этими методами абсолютный (глобальный) экстремум даже при не заданной аналитически целевой функции. Они позволяют получить решение многих задач на ЭВМ быстрее, чем другие методы, но не всегда гарантируют достижение положительных результатов.

Эвристическое программирование основано на использовании опыта специалистов, который формируется в виде правил, эмпирических зависимостей и схем вычислений. Особенно перспективно эвристическое программирование для решения инженерных задач, и в частности, при конструировании ЭА: выбор структурных схем аппаратуры и ее отдельных частей; распределение функций между аппаратурой и операторами; оценка качества аппаратуры (метод экспертных оценок) и др.

Все рассмотренные методы оптимизации относятся к области детерминированных (неслучайных) функций и процессов. Однако в практике проектирования приходится решать задачи также стохастического программирования, т.е. оптимизировать случайные величины и функции. Стохастическое программирование дает методы решения условных экстремальных задач при неполной информации о параметрах исследуемого процесса.

Выбор метода оптимизации в каждом конкретном случае определяется рядом факторов:

• способом осуществления оптимизации (вручную или автоматически);

• объемом имеющейся в нашем распоряжении информации об объекте оптимизации;

• вопросом о том, имеем ли мы оптимум на протяженном интервале или в одной определенной точке, т.е. для конечного момента времени.