232

В ЦФ осуществляется цифровая обработка сигналаu_Цвх, представленного набором кодовых символов, соответствующих системе представления чисел в данном вычислительном средстве (обычно в двоичном коде). Тактовая частота ЦФ равна или кратна частоте дискретизации по времени 1/Т. Сигнал u_Цвых, обработанный по заданному алгоритму, с выхода ЦФ поступает на ЦАП, где преобразуется в последовательность ступенек u_А(t), величины которых пропорциональны соответствующим значениям цифрового сигнала u_Цвых. Ступенчатое напряжение u_А(t) сглаживается аналоговым ФНЧ, на выходе которого восстанавливается аналоговый сигнал u_Авых (t).

В цифровых системах передачи информации сигнал с выхода приемника снимается непосредственно в цифровой форме. При этом отпадает необходимость в блоке АЦП. В определенных случаях потребитель информации использует обработанный сигнал также в цифровой форме, при этом отпадает необходимость и в блоке ЦАП.

Ниже приводятся необходимые для изложения вопросов цифровой фильтрации сведения о дискретных сигналах и дискретных цепях, а также обсуждаются структуры и методы синтеза цифровых фильтров.

17.2. Характеристики дискретных сигналов

Сигналы, обрабатываемые в ЦФ, дискретны по времени, квантованы по уровню и представлены цифровым кодом. Кроме этого, все коэффициенты математических операций (коэффициенты фильтра), которым подвергается сигнал в ЦФ, также квантованы. Учет квантованности сигналов и коэффициентов усложняет анализ работы цифровых систем. Поэтому обычно анализ разбивается на два этапа. На первом этапе сигналы считаются дискретными, но не квантованными (шаг квантования бесконечно мал). Также предполагается, что коэффициенты фильтра могут принимать любые значения в заданном диапазоне (все значения х на числовой оси в диапазоне от х₁ до х₂). В данной главе будем исходить из допущения, что в ЦФ вводятся неквантованные отсчеты (в аналоговой форме), над которыми и совершаются математические операции (существуют дискретные системы аналогового типа, в которых не используется цифровое кодирование).

На втором этапе анализа учитывается квантованность сигналов и коэффициентов фильтра и определяются погрешности из-за квантования и округления (шумы квантования). Этот анализ в данной главе не приводится.

Дискретные сигналы так же, как и аналоговые, могут быть представлены несколькими способами во временной и частотной областях. Наибольшее распространение получили представления дискретных сигналов в виде дискретных последовательностей(временная область) или в спектральной форме, например, в видедискретного преобразования Лапласа, в видеz-преобразованияи в формедискретного преобразования Фурье.Рассмотрим основные свойства дискретных сигналов при различных формах их описания.

Дискретные последовательности. Подобные сигналы являются выборками аналогового сигнала s (t) в моменты времени t = nТ и обозначаются символом s (nT). Введем следующие обозначения и поясним смысл новых переменных: ωt = kω_m nT= = k = k n . Здесь Т_с ­= NT – длительность обрабатываемой реализации сигнала, N ­= – база сигнала, а k и n – натуральные числа, имеющие соответственно смысл нормированной частоты и нормированного времени .

Представление дискретного сигнала дискретной последовательностью подобно временному представлению аналогового сигнала.

Рассмотрим простейшие дискретные последовательности, которые широко используются при анализе цифровых систем:

а) единичный импульс δ(n) (рис. 17.3):

В дискретных системах единичный импульс играет такую же роль, какδ-функция в аналоговых системах;

б) единичный импульс, задержанный на n₀ тактов (рис. 17.4):

Любой дискретный сигналs(n) может быть выражен дискретной сверткой вида

s (n) = .(17.3)

в) единичный скачок σ (n) (рис. 17.5):

Единичный скачок связан с единичным импульсом соотношением

σ (n) = ;(17.5)

г) дискретный гармонический сигнал (рис. 17.6).

Выборки из непрерывного сигнала s (t) = cos ω_с t описываются дискретной последовательностью

s (nT) = cos ω_с nT , (17.6)

где ω_с = 2π / Т_с;Т_с– период функции; либо числовой последовательностью, получаемой подстановкойω_с = 2π / Т_с:

s(n)= =cosn (17.7) для всехn, гдеN = Т_с / Т – база сигнала или целое число тактов, составляющих период дискретного гармонического сигнала;

д) дискретная комплексная экспонента

s (n) = exp (јn) = cos n + j sin n для всех n; (17.8)

е) дискретная степенная функция(рис. 17.7):

Дискретное преобразование Лапласа.Прямое дискретное преобразование Лапласа последовательностиs (nТ) определяется формулой

S_Д (p) = ₤{s (nТ)} = ,(17.10)

где p = σ + jω – комплексная переменная.

Обратное дискретное преобразование Лапласа восстанавливает дискретную последовательностьs (nТ) по ее изображению:

s (nТ) = ₤^-1{S _Д (p)} = . (17.11)

Найдем в качестве примера изображение по Лапласу для дискретной степенной последовательности (17.9) приа < 1.

Используя формулу (17.10), получим

S _Д (p) = =.

Здесь на плоскости комплексной переменной p = σ + jω имеется один полюср₁ = ln a, который приа < 1 расположен в левой полуплоскости, что соответствует затухающей последовательности.

Изображения по Лапласу дискретных последовательностей, в которые входит функция e ^pT, являются трансцендентными функциямир, что затрудняет анализ. Поэтому, полагаяe ^pT=z, вместо преобразования Лапласа пользуются z-преобразованием.

z-преобразование. По определению, прямоеz-преобразование для последовательностиs (nТ) дается выражением

S (z) = Z {s (nТ)} = . (17.12)

Комплексная функция S (z) определена только для областиz, в которой степенной ряд (17.12) сходится.

Обратное z-преобразование определяется формулой

s (nТ) = Z ^-1{S (z)} = . (17.13)

В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуруСв области сходимости, охватывающему начало координат. Интеграл (17.13) может быть вычислен при помощи теоремы о вычетах, а именно

s (nТ) = ∑ res S (z) z ^n-1 | _{z внутри С} .

Рассмотрим некоторые важные свойства z-преобразования:

а) линейность.ЕслиХ₁ (z) иХ₂ (z) являютсяz-преобразованиями последовательностей х₁(n) и х₂(n), то при любых действительных а₁ и а₂ ,

z-преобразование последовательности

х₃(n) = х₁(n) +х₂(n) (17.14)

равно

Х₃ (z) =а₁ Х₁ (z) +а₂ Х₂ (z) ; (17.15)

б) задержка.Если последовательностьх₁(n) имеетz-преобразованиеХ₁ (z), тоz-преобразованиеХ₂ (z) последовательностих₂(n) = х₁(n – n₀), задержанной наn₀ элементов, при любыхn₀ равно

Х₂ (z) = Х₁ (z) . (17.16)

Это свойство используется при решении разностных уравнений. Например, разностное уравнение

y₂(n) = х₁(n) –b₁y₂(n – 1) – b₂y₂(n – 2)

можно подвергнуть z-преобразованию

Y (z) =Х (z) – b₁ z ^–1 Y (z) – b₂ z ^–2 Y (z),

откуда

Y (z) = , гдеY (z) = ,X (z) = ;

в) свертка последовательностей.Если последовательностиs₁(n) соответствуетz-преобразованиеS₁ (z), а последовательностиs₂(n) –S₂ (z), то свертке последовательностей

s₃(n) = (17.17)

отвечает произведение их z-преобразований

S₃ (z) = S₁ (z) S₂ (z). (17.18)

Найдем z-преобразования для некоторых дискретных последовательностей:

а) единичный импульс(17.1), см. рис. 17.3. Посколькуδ(n) = 0 при любых n , за исключением n = 0, гдеδ (n) = 1, тоS (z) = 1;

б) единичный скачок σ (n) (17.4), см. рис. 17.5:

S (z) = =;

в) дискретное одностороннее гармоническое колебание

s (n) = σ (n) cos n (17.7), см. рис. 17.6.

Так как s (n) = σ (n) cos n = σ(n), то

S (z) = = ;

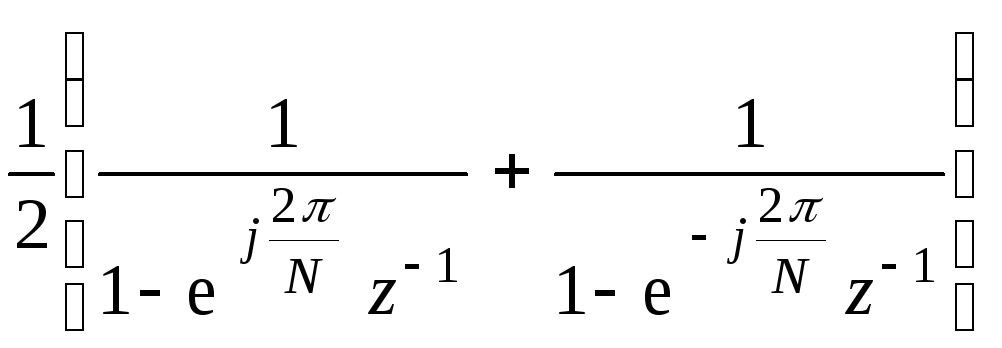г) дискретная комплексная экспонентаs (n) = σ (n) exp (јn) (17.8);

S (z) = = ;

д) дискретная степенная функция(17.9), см. рис. 17.7:

S (z) = .

Дискретное преобразование Фурье (ДПФ).Периодическая последовательность и последовательность конечной длины могут быть представлены дискретным рядом Фурье.

Рассмотрим периодическую последовательность х_N (n) с периодом в Nотсчетов. Запишем ее в виде ряда Фурье

x_N (n) = , (17.19)

где частоты спектральных составляющих, образующих x_N (n), могут принимать только значения n k (– ∞ < k < ∞ ), кратные N. Коэффициенты G_N (k) представляют амплитуды гармоник с частотамиn k . Так как функцияявляется периодической с периодомN,т.е.

, (–∞ < m < ∞ ),(17.20)

то ряд (17.19) приводится к более привычному виду

x_N (n) = , (n = 0, 1, 2, …, N –1). (17.21)

Формула (17.21) носит название обратного дискретного преобразования Фурье (ОДПФ).

Прямое дискретное преобразование Фурье (ДПФ) определяет дискретный спектр G_N (k) периодической последовательностиx_p (n):

G_N (k) = , (k = 0, 1, 2, …, N – 1). (17.22)

Из (17.21) и (17.22) следует, что обе последовательности x_N (n) иG_N (k) периодичны с периодом изNэлементов. При этомG_N (k) полностью определяется одним периодомx_N (n).

Найдем связь дискретного спектраG_N (k) периодической по­следовательностиx_N (n) со спек­тром конечной после­дова­тельно­стиx (n) (17.23),

равной од­ному пе­риоду пе­риодиче­ской по­сле­довательно­сти, где x (n) имеетNэлемен­тов (рис. 17.8).

Применим к последователь­но­сти x(n) z-пре­образование (17.12):

Х (z) = Z{х (n)} = =. (17.24)

Вычисляя сумму (17.22) при z=, находим

Х (z) = Х ()= . (17.25)

Сравнивая (17.25) и (17.22) и учитывая, что x_N (n) = x (n) на интервале 0 ≤n ≤ N – 1 , получаем

G_N (k) = Х () . (17.26)

Итак, коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой последовательности вNточках. Кроме того, существенно, что коэффициенты ДПФ последовательности конечной длины однозначно определяют саму последовательность, которую можно получить, пользуясь формулой (17.21) ОДПФ. Хотя ДПФ и ОДПФ вводятся для периодических последовательностей, они могут быть использованы для представления последовательностей конечной длины.