ртцис

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(t)= lim s4

(t)= lim e−α

.pdf

Скачиваний:

165

Добавлен:

11.05.2015

Размер:

5.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 268 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Пример 3.2 - Расчет спектральной плотности одиночного экспоненциального импульса, его четной и нечетной составляющих, изображенных на рисунке 3.3.

s(t) E	sчет(t)	E	2	sнеч(t)	E	2
			2			2
	0		t	0		t
	t
а)	б)			в)

Рисунок 3.3 − Экспоненциальный импульс s(t), его четная sчет(t) и нечетная sнеч(t) составляющие

Математическое описание экспоненциального импульса имеет вид s(t)= Ee−α t , t ≥ 0 .

Разделяясигналобщеговиданачетнуюинечетнуюкомпоненты, получим: sчет(t)= 12 [s(t)+ s(−t)]= E2 e−α t ,

sнеч(t )=

1 [s(t)

− s(−t)]= E e−α

sign(t).

Суммирование четной и нечетной составляющих приводит к восстанов-

лению сигнала общего вида:s(t)= sчет(t )+ sнеч(t),

s(t )=

e−α

[1+ sign(t)]= Ee−α t

, t ≥ 0 .

Спектральная плотность экспоненциального импульса равна

∞

e−(α+ jω)t

∞

S&(ω)= ∫Ee−α t e− jω t =

− (α

jω)

α + jω

Спектральная плотность состоит из суммы действительной и мнимой

частей

E(α − jω)

S&(ω)=

= E

− jE

α2 +ω2

α + jω

α2 +ω2

Мнимая часть спектральной плотности соответствует нечетной составляющей сигнала sнеч(t), а действительная часть спектральной плотности от-

носится к четной составляющей сигнала. Результаты расчетов сведены в таблицу 3.2.

Таблица 3.2 − Временное и спектральное представления сигнала общего вида и его составляющих

	Сигналы		Спектральные плотности
Аналитическое	Графическое	Аналитическое		ω	−	АЧХ,	ϕ ω −	ФЧХ
представление	представление	представление		\|S( )\|		АЧХ,	( )	ФЧХ
представление	представление	представление
	E			АЧХ			E/α
	E			АЧХ
s(t )= Ee−α tσ(t)		Ф+[s(t )]=	E	ФЧХ
			α + jω
	0	t				0		ω
	0	t					E/α
							E/α

sчет(t )=

−α

E/2

Ф+[s

чет

(t )]= E

α2 +ω2

ϕ(ω)=0 0

E/2α

sнеч(t )=

e−α

sign(t )

E/2

Ф+[sнеч(t )]= − jE

-E/2

+ω

π/2

-π/2 ω

Анализируя спектральные характеристики, замечаем:

а) спектральнаяплотностьвточке ω = 0 численноравнаплощадисигнала

∞

∫Ee−α t dt =

αE ,

∫

E2 e

−α

dt =

αE ,

∫E2 e

−α

sign(t)dt = 0 ;

−∞

б) спектральная плотность затухает с увеличением частоты без “пульсаций”, т.к. исследуемые сигналы имеют конечную энергию, но бесконечную теоретическую длительность.

В таблице 3.3 представлены аналитические и графические модели различных сигналов во временной и частотной областях.

3.5 Энергетические характеристики непериодических сигналов

Энергию непериодического сигнала можно определить как по временному, так и по спектральному представлениям:

∞

Э = ∫s2 (t)dt ,

−∞

∞

Э = ∫ s(t)

∫S&(ω)e jω t dωdt =

∫ S&(ω) ∫s(t)e jω t dtdω =

2π

−∞

14243

S&* (ω)

∞

∫S&(ω) S&*(ω)dω ,

2π

−∞

∞

2 dω =

∞

2 dω .

Э =

∫

S&(ω)

∫

S&(ω)

2π

−∞

(3.26)

(3.27)

Квадрат модуля спектральной плотности сигнала называется энергетическим спектром WS (ω):

WS ( )

( )

(3.28)

Реальные сигналы имеют не только конечную энергию, но и ограниченную длительность, а, следовательно, – бесконечный спектр. На практике требуется не только определить полную энергию сигнала, но и оценить практическую полосу частот, занимаемую сигналом. Для принятия объективного решения используют энергетический критерий: вводят коэффициент использования λ энергии сигнала. Выбирают значение коэффициента использова-

ния λ = 0,9 ÷0,99.

Под шириной спектра понимают эффективную полосу частот ∆ωЭ, в

пределах которой сосредоточена основная часть энергии сигнала ( 90% ÷99%), и рассчитывают ее из уравнения

∆ω

∞

Эλ =

∫

S&(ω)

2 dω = λ

∫

S&(ω)

2 dω .

(3.29)

Временное представление сигнала также не всегда определено конечной длительностью импульса. Например, сигнал, представляющий собой разряд конденсатора через резистор (экспоненциальный импульс), имеет бесконечную длительность. Поэтому для сигналов также вводят понятие энергетической (эффективной) длительности τЭ. Энергетической длительностью τЭ

называют интервал времени, в пределах которого заключена основная часть энергии сигнала. Коэффициент, обозначающий учитываемую часть энергии, обозначим так же λ . Для расчета энергетической длительности сигнала используют уравнение

t1	+τЭ	∞
Эλ =	∫	s2 (t)dt = λ ∫s2 (t)dt .	(3.30)
	t1	−∞

Пример 3.3 − Расчет энергетических параметров одиночного экспоненциального импульса

Математическое описание экспоненциального импульса во времени и его спектральная плотность известны из примера 3.2. Графические модели имеются в таблице 3.2. Откуда

s(t) = Ee−α t , t ≥ 0 ,

S&(ω)= α +Ejω ,−∞ <ω < ∞.

Учитываемая часть энергии λ составляет 90% . Для определения энергетической длительности τЭ воспользуемся уравнением (3.30):

	∞					τ
0,9 ∫E2e−2α t dt =						∫ЭE2e−2α t dt ;
	0		∞			0		τЭ
0,9	E2	e−2α t		=		E2	e−2α t		;
	E2					E2
	− 2α
	− 2α		0			− 2α		0
			0					0
		0,9 =1 − e−2α τЭ ;
		ln10			=1,15α .
		τЭ = 2α			=1,15α .

Для определения энергетической полосы частот ∆ωЭ воспользуемся уравнением (3.29):

∞

∆ω

E 2

0,9

∫

dω

∫

dω ;

+ω

∞

∆ωЭ

0,9 1 E2

= 1 E2

arctgω

arctg

;

0,45

1 arctg

∆ωЭ

;

6,3

∆ω

=α tg(0,9

) ≈ 6,3α ; ∆f

α ≈α .

2π

Энергетические параметры экспоненциального импульса показаны на рисунке 3.4.

s(α t) E

0,61 E

0,316 E

0,22 E

0	0,5		1,5 α t
		1
	τЭ =1,15 α

S&(ω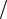α) Eα

0,707 Eα

0,45 Eα

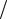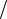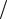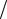0,157 Eα

0 1 2 3 4 5 6 ω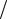α ∆ωЭ = 6,3 α

Рисунок 3.4 – Энергетические параметры одиночного экспоненциального импульса

3.6Границы применимости преобразований Фурье

ивозможности их расширения

Преобразования Фурье связывают между собой спектральную плотность S&(ω) и непериодический сигнал sT (t), полученный из периодического при T →∞, поэтому

lim		s(t)= 0 .	(3.31)
t	→∞

Результаты анализа ряда типовых интегрируемых сигналов приведены в таблице 3.3.

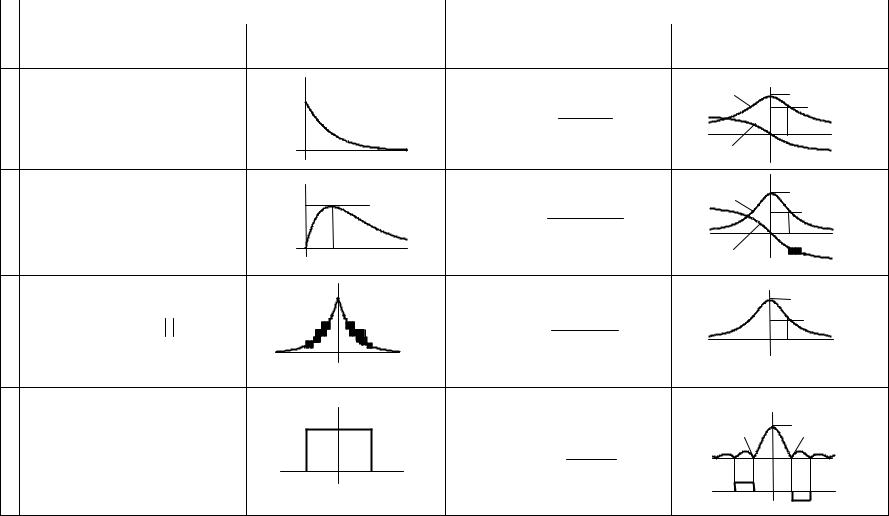
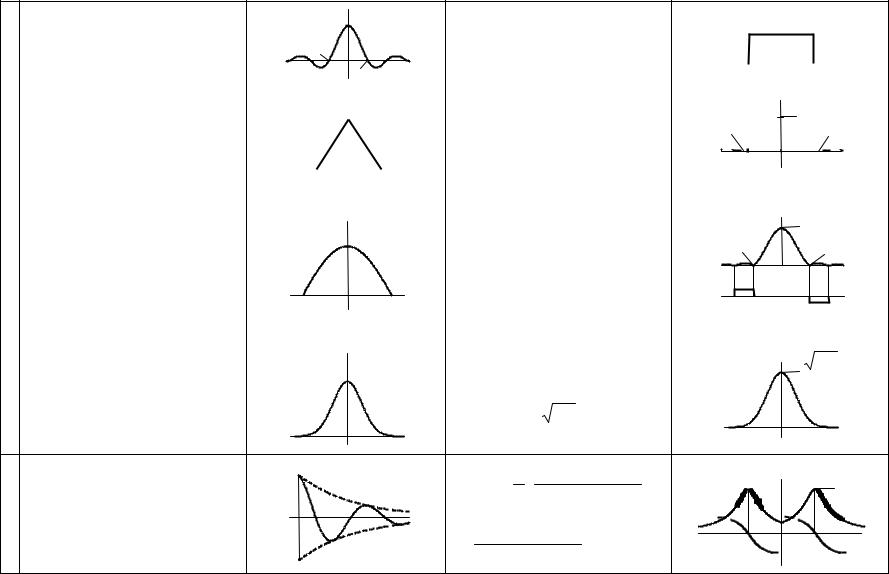
Таблица 3.3 − Преобразование Фурье абсолютно интегрируемых сигналов

Сигнал s(t)			ω
		Спектральная плотность S( )
Аналитическое	Графическое	Аналитическое	\|S(ω)\| −АЧХ,	ϕ(ω) −ФЧХ
представление	представление	представление	\|S(ω)\| −АЧХ,	ϕ(ω) −ФЧХ
представление	представление	представление

s(t)

АЧХ

1/α

s(t )= e−α tσ(t)

S&(ω) =

π/2

0.7/α

α + jω

ω-π/2

ФЧХ0

s(t)

1/αe

АЧХ

1/α2

s(t )=te−α tσ(t)

S&(ω) =

0.5/α

(α + jω)2

ФЧХ 0

1/α

-π

s(t)

2/α

2α

1/α

s(t)=e−α t

S&(ω) =

α2 +ω2

ϕ(ω)=0

s(t)

sin ωτ

1,| t |≤

-2π/τ

2π/τ

s(t)=

(ω)=τ

-τ/2 0

ωτ

0,| t |>

τ/2 t

sinωmt

s(t)

,| ω |<ωm

ϕ(ω)=0

π/ωm

s(t )=

-π/ωm

S&(ω) = ωm

ωmt

π ω

0,| ω |>ωm

ω ω

t |

s(t)

ωτ

1 −

,| t

|≤

sin

-4π/τ

4π/τ

/ 2

s(t )=

S&(ω)= τ

ωτ

0,| t |>

/2 0

ϕ(ω)=0

cos(ωot ),| t |≤

s(t)

2τ/π

ωτ

-3π/τ

3π/τ

s(t )=

cos

0,| t |>

S(ω) = 2ωo

ωo2 −ω2

τ =

-τ/2 0

τ/2 t

0 -π

ωo

t 2

s(t)

−σ 2ω2

2π

−

s(t )=e

2σ 2

S&(ω) =σ 2πe

ϕ(ω)=0

s(t)

S&(ω) =

1/2α

−ωo )

π/2

s(t )

−αt

cos

α + j(ω

ot)

(t)

-ω0

ω0

α +

j(ω

+ωo )

-π/2

Первое условие (3.31) следует трактовать как конечность переходных процессов в линейных системах.

∞
∫s(t )dt ≤ M	(3.32)

−∞

Второе соотношение (3.32) свидетельствует о конечности энергии сигнала или является условием его физической реализуемости.

Условия Дирихле (3.31) и (3.32) значительно снижают класс сигналов, к которым применимы преобразования Фурье. Однако, точно также как к непериодическим сигналам были применены ряды Фурье (и в результате получены преобразования Фурье), к периодическим сигналам применяют преобразования Фурье.

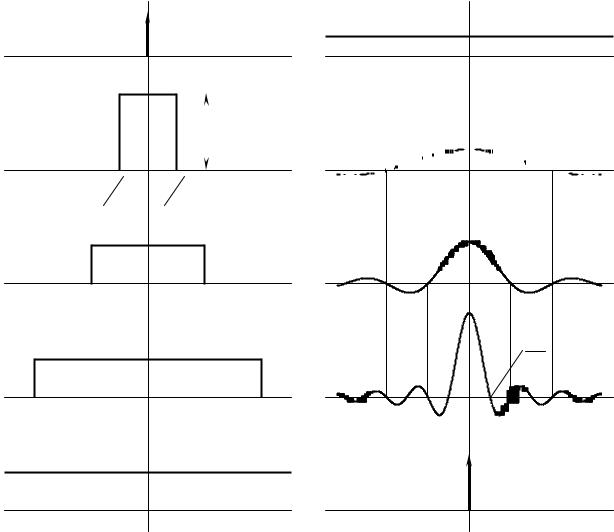
Рассмотрим изменения спектральной характеристики одиночного прямоугольного импульса (рисунок 3.5) в двух предельных случаях:

во-первых, при увеличении длительности импульса до бесконечности (переход к постоянной составляющей);

во-вторых, при уменьшении длительности импульса до нуля при одно-

∞

временном сохранении площади импульса ( ∫s(t)dt =1) .

−∞

К аппарату обобщенных функций, в частности к дельта – функциям, приходится обращаться в двух идеальных моделях: при τ →0 и при τ →∞. Только при τ →0 дельта – функция возникает во временной области, а при τ →∞ дельта−функция образуется в частотной области.

Применяя фильтрующее свойство дельта–функций при выполнении преобразований Фурье, получим:

∞

Ф+[δ(t)]= ∫δ(t)e− jω t dt =1, − ∞ <ω < ∞;

−∞

∞

Ф−[2π δ(ω)]= 21π −∫∞2π δ(ω)e jω tdω =1, −∞ <t < ∞.

Спектральная характеристика дельта–функции равна 1 на всех частотах, т.е. полоса частот равна бесконечности. Спектральная характеристика постоянной составляющей равна 2π δ(ω), т.е. равна бесконечности при ω = 0 и равна нулю на всех других частотах.

		δ(t)					1
	0					t	0				ω
					1		1		2π
					1
				τи
				τи						τ
						t						ω
−τ	0	τ	2					0
−τ	0	τ						0
	2

		E			2Eτ	π
						π
						τ
−τ	0	τ	t	0	4Eτ		ω
		E				π
		E				2τ
						2τ
− 2τ	0	2τ	t	0			ω
		E =1			2π δ(ω)
		E =1
	0		t	0			ω

Рисунок 3.5 − Временное и спектральное представления процесса преобразования одиночного импульса в дельта−функцию и постоянную составляющую

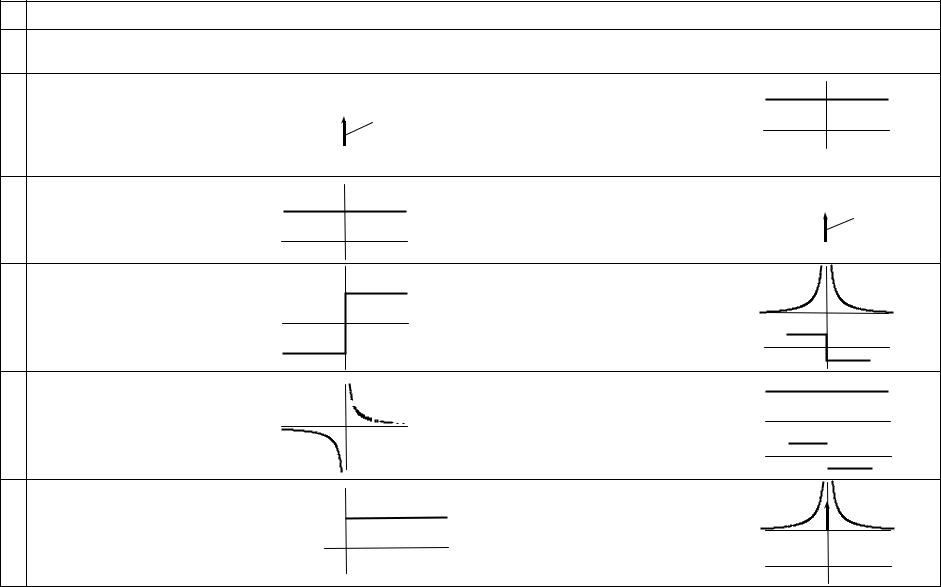
3.7 Спектральное представление некоторых неинтегрируемых сигналов

Условие абсолютной интегрируемости сигналов можно не нарушать, если предварительно преобразовать неинтегрируемый сигнал. На рисунке 3.6 показаны неинтегрируемые s1(t), s2 (t) и интегрируемые сигналы s3 (t), s4 (t):

s	(t )= lim s	3	(t )= lim e−α	t	,


1	α→0		α→0

Результаты анализа ряда типовых неинтегрируемых сигналов приведены в таблице 3.4.

Таблица 3.4 − Преобразования Фурье сигналов, описываемых обобщенными функциями

Сигнал s(t)

Спектральная плотность S&(ω)

Аналитическое

Графическая модель

Аналитическое описание

|S&(ω) |-АЧХ, ϕ(ω)-ФЧХ

описание

s(t )=δ(t )

s(t)

δ(t)

S&(ω) =1

ϕ(ω)=0

s(t )=1

s(t)

S&(ω) = 2πδ(ω)

2πδ(ω)

s(t )= sign(t )=

s(t)

| t |

S&(ω) =

jω

-1

s(t )=

s(t)

S&(ω) = − j sign(ω)=

= −

jω

π t

π/2

ω |

s(t)

S&(ω) =πδ(ω)+

s(t )=σ(t )

jω

π/2

<<< < Предыдущая 1 2 3 4 5 6 78 / 268 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.05.2015300.03 Кб18РИМСКОЕ ПРАВО КОПЫЛОВ.doc
#
08.09.201935.05 Кб0римское право лекция.docx
#
30.08.2019521.22 Кб0Романова курсач.doc
#
26.11.2019390.66 Кб1Романский и готический стиль.doc
#
21.11.2019126.98 Кб0РП практики преддипломной.doc
#
11.05.20155.51 Mб165ртцис.pdf
#
10.05.201590.11 Кб6РУДН_Свободные зоны.doc
#
11.05.20151.28 Mб118Руководство по решению дискретки.pdf
#
11.05.2015146.3 Кб31СА реферат.docx
#
10.05.2015409.6 Кб87САПР реферат.doc
#
19.11.20193.44 Mб59сб.зад.ант иус свч 1.doc