3289-electrodinam

Подставляя (6.31) в (6.30) и переходя от векторного уравнения к трем скалярным, получим:

Будем пренебрегать в (6.32) эффектами второго порядка малости, Hm << H0 , Mm << M0 , то есть произведением малых вели-

чин:

141

Перейдем к более компактному виду:

и подставим в него значение проекций вектора Мm :

В уравнениях (6.38) сгруппируем слагаемые перед одноименными проекциями напряженности магнитного поля:

Введем дополнительные обозначения:

μ0 (1 − A)= μx ; μ0C = a.

Сопоставление (6.39) и (6.3) дает тензор вида

Полученный тензор содержит симметричные недиагональные элементы, отличающиеся знаком, и, следовательно, намагниченный

142

постоянным магнитным полем феррит — гиротропная среда. Как это влияет на распространение электромагнитных волн, рассмотрим ниже.

6.4. Плазма в электромагнитном поле

6.4.1. Общие свойства плазмы

Плазмой называется электрически нейтральный газ, в котором значительная часть атомов или молекул ионизирована. По целому ряду свойств плазма отличается от обычных газов, содержащих одни нейтральные молекулы. Так, например, благодаря наличию свободных зарядов плазма обладает большей, чем у обычных газов, электрической проводимостью. Под влиянием постоянного магнитного поля она может проявлять анизотропные свойства и т.п. В связи с этим целесообразно рассмотреть процессы, протекающие в плазме под действием электромагнитных полей.

В плазме возможны взаимодействия электронов и ионов с электрической и магнитной составляющими приложенного к ней электромагнитного поля. По своей величине они неравноценны. В большей части радиотехнического диапазона частот движение тяжелых ионов практически не влияет на распространение электромагнитных волн в плазме. Поэтому в дальнейшем их принимать в расчет не будем.

Сравним теперь силу взаимодействия электронов с электрической и магнитной составляющими электромагнитного поля, то есть найдем отношение величины силы Лоренца FЛ к силе Кулона FК.

Пусть электрон, имеющий заряд е0 , движется со скоростью V пер-

пендикулярно линиям вектора магнитной индукции B . Имея в виду только модули векторов, запишем:

143

Проведя ряд очевидных преобразований, убеждаемся, что от-

ношение рассматриваемых сил значительно меньше единицы, т.е.

FК >> FЛ.

Таким образом, будем учитывать только взаимодействие электронов с электрической составляющей переменного электромагнитного поля.

6.4.2. Диэлектрическая проницаемость плазмы в переменном электромагнитном поле

Как отмечалось, плазма содержит большое число заряженных частиц, которые в отсутствие постоянного магнитного поля (ненамагниченная плазма) движутся хаотически. Под влиянием электрического поля с напряженностью E = E0 cos ωt на каждый свободный электрон действует сила

FК = −e0 E.

Представим силу как произведение массы электрона т0 на

ускорение и, пренебрегая соударениями электронов с другими частицами, получим уравнение движения

где r — смещение электрона относительно исходного положения. Решая уравнение (6.41), находим

Таким образом, электроны совершают прямолинейное колебательное движение в направлении вектора E , приобретая при этом электрический момент

144

Если в единице объема плазмы имеется N свободных электронов и каждый из них получает одинаковое смещение, то электрический момент единицы объема (вектор электрической поляризации) равен

Электрическая восприимчивость и диэлектрическая проницаемость соответственно равны:

Ne2

χэ = − 0 ; (6.46)

ε m ω2

0 0

Ne2

ε =1 − 0 . (6.47)

ε0m0ω2

Отсюда следует, что диэлектрическая проницаемость ненамагниченной плазмы скалярная величина. Вектор электрической индукции в этом случае совпадает по направлению с вектором напряженности электрического поля и плазма является изотропной средой.

Пусть наряду с полем E = E0 cos ωt на плазму воздействует постоянное магнитное поле H0 = z0 H0 . Теперь, как только под

влиянием электрического поля электрон приобретает скорость V , на него начинает действовать со стороны магнитного поля сила Лоренца

Из формулы (6.48) видно, что величина и направление силы Лоренца будут зависеть от взаимной ориентации векторов V и H0 .

Предположим сначала, что, после того как электрону была сообщена начальная скорость V0 , вектор которой параллелен E0 ,

145

электрическое поле исчезает. Тогда в зависимости от направления вектора E по отношению к H0 электроны будут перемещаться по различным траекториям.

Если E H0 , то согласно (6.48) сила Лоренца FЛ = 0 и частицы двигаются прямолинейно вдоль силовых линий постоянного магнитного поля H0 (как и при его отсутствии).

При E H0 сила Лоренца имеет максимальное значение

FЛ = e0μ0V0 H0.

Теперь в любой точке траектории электрона сила FЛ перпен-

дикулярна вектору скорости (рис. 6.5,а). Следовательно, она не производит работу и может изменять лишь направление скорости, не изменяя ее величины, поэтому электроны будут двигаться по окружностям, плоскости которых перпендикулярны вектору H0 . Ра-

диус окружности можно определить из условия равенства центробежной силы и силы Лоренца:

m v2

0r 0 = e0μ0V0 H0 ,

Период обращения электрона по окружностям Tm находится из очевидного соотношения V0Tm = 2πr , откуда с учетом (6.49) будем иметь

Tm = 2μπm0 .

e0 0 H0

Угловая скорость вращения электрона (частота гиромагнитного резонанса) равна

146

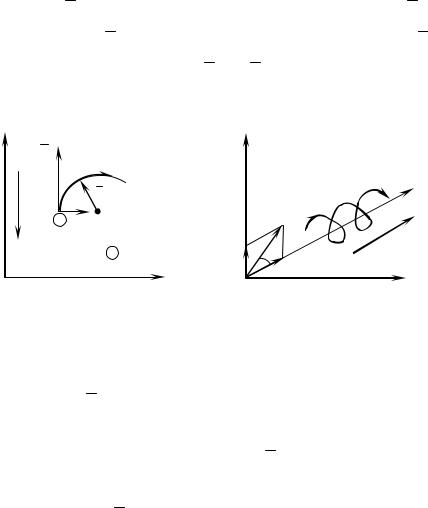
Если вектор E (следовательно, начальная скорость V0 ) составляет с направлением H0 некоторый угол α, то скорость V0 можно разложить на две составляющие: V и V (рис. 6.5,б).

Рис. 6.5. Виды траектории движения свободных электронов в намагниченной плазме

Под влиянием V электрон приобретает вращательное движение. Одновременно с этим он скользит вдоль силовых линий магнитного поля с постоянной скоростью V . Результирующая траектория электрона будет иметь вид винтовой линии с осью, параллельной вектору H0 .

6.4.3. Тензор диэлектрической проницаемости намагниченной плазмы

Пусть теперь переменное электрическое поле не исчезает после того, как электроны начали движение. Уравнение движения электрона при одновременном воздействии переменного электрического поля и постоянного магнитного поля может быть получено из формулы (6.41) путем введения в правую часть силы Лоренца. В комплексной форме уравнение принимает вид

где r = rme jωt .

147

Тогда

Умножим правую и левую части равенства (6.51) на e0 N2 . Те- m0ω

перь легко получить комплексную амплитуду вектора поляризации:

Перейдем от векторного уравнения (6.52) к системе скалярных уравнений:

Выразим проекции вектора электрической поляризации через проекции вектора напряженности электрического поля:

148

Комплексная амплитуда вектора электрической индукции определяется равенством

Вновь переходя к системе скалярных уравнений, с учетом обозначений, показанных в (6.45) фигурными скобками, получим:

Введем обозначения:

Сравнивая уравнения (6.56) с (6.3), с учетом обозначений (6.57) получим выражение для тензора диэлектрической проницаемости намагниченной плазмы

149

Таким образом, по внешнему виду тензоры μˆ для намагниченного феррита и εˆ для намагниченной плазмы симметричны. Это дает возможность при исследовании полей воспользоваться принципом перестановочной двойственности.

6.5. Продольное распространение плоских электромагнитных волн в феррите

Пусть электромагнитная волна распространяется в феррите в направлении постоянного магнитного поля H = z0 H0 . Так как на-

пряженность поля вдоль координат x и y в приближении плоских волн не изменяется, то

∂∂x = ∂∂y = 0 .

Мы должны определить все основные характеристики электромагнитных волн: поляризацию, фазовую скорость, волновое сопротивление. Прежде всего необходимо получить дисперсионные соотношения.

Для этого запишем уравнения Максвелла:

Перейдем к скалярной форме записи:

∂H∂ymz − ∂H∂zmy = jωεEmx ;

0

∂H∂zmx − ∂H∂xmz = jωεEmy ;

0

∂H∂xmy − ∂H∂ymx = jωεEmz ;

0 0

150