
теория вероятностей
.pdf
61
|
σ |
|
|
|
|
. Поэтому доверительная вероятность |
|
ление с параметрами: X ~ N a, |
|
|
|
|
n |
|
|
γ удовлетворяет соотношению (используем формулу (4.2)):
|
|
|
|
|
|
ε |
|
|
ε |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
n |
. (5.2) |
||
γ = P |
| a−a |< ε |
= P(| X −a |< ε)= 2Φ |
|
|
= 2Φ |
|
σ |
|
||||
|
|
|
|
|
|
σ( X ) |
|
|
|
|
||
В этом соотношении неизвестной величиной является точность оценки ε.
Обозначим uкр = εσ n , отсюда
n , отсюда
ε = uкр σ . |
(5.3) |
n |
|
Значение uкр найдем с помощью таблицы функции Лапласа (приложе-
ние 1), учитывая, что Φ(uкр) = 2γ .
Доверительный интервал для генерального среднего будет иметь вид
|
σ |
|
σ |
|
|
|
; x +uкр |
|
(5.4) |
||
x −uкр |
n |
|
. |
||
|
|
n |
|
||
Этот метод построения доверительного интервала применяется и в случае, если генеральная совокупность Х не является нормальной. Согласно центральной предельной теореме, для выборки достаточно большого объема вы-
борочное среднее X будет иметь приближенно нормальное распределение с параметрами M ( X ) = a и σ( X ) = σn , где a и σ — соответствующие
параметры генеральной совокупности. В этом случае для построения доверительного интервала используют формулу (5.4), определяя значение uкр по
таблицам функции Лапласа, если n > 30. При n ≤ 30 значение uкр заме-
няют на tкр, которое определяют по таблице распределения Стьюдента (приложение 3), и формула (5.4) принимает вид:
|
|
|
σ |
; x +t |
|
|
σ |
|
(5.5) |
x −t |
кр |
|
кр |
|
, |
||||
|
|
n |
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
где tкр = t(k; α), k = n −1, α =1 − γ (область двусторонняя).
Если значение параметра σ неизвестно, то доверительный интервал строят по формуле (5.5), заменяя параметр σ с его оценкой
62
|
1 |
n |
(xi − x)2 . |
|
s = |
∑ |
|||
|
||||
|
n −1 i=1 |
|
||
Величина σ называется средней ошибкой выборки и зависит от спо-
 n
n
соба отбора: в случае конечной генеральной совокупности объема N вносится
«поправка на бесповторность отбора», равная |
1 |
− |
n |
(табл. 5.1). |
||||
|
|
|
N |
|
|
|||
|
|
|
|
|
|
|
Таблица 5.1 |
|
|
|
|
|
|
|
|
|
|
|
Средняя ошибка выборки для генерального среднего |
|||||||
|
|
|
|
|
|
|
|
|
|
Генеральная |
Бесконечная |
|
|
|
Конечная |
||
|
совокупность |
|
|
|
объема N |
|
||
|
|
|
|
|
|
|||
|
Тип отбора |
Повторный |
|
|
Бесповторный |
|
||
|
Средняя ошиб- |
σ |
|
|
|
σ |
n |
|
|
ка выборки |
n |
|
|
|
n |
1 − N |
|
Пример 1. Служба контроля Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. С помощью случайного отбора было выбрано 10 квартир и определен расход элек-
троэнергии в течение одного из летних месяцев (кВт ч) : 125, 78, 102, 140, 90,
45, 50, 125, 115, 112.
С вероятностью 0.95 определите доверительный интервал для среднего расхода электроэнергии на одну квартиру во всем доме при условии, что отбор был: а) повторным; б) бесповторным, и в доме имеется 70 квартир.
Решение. По условию задачи объем выборки n =10, т.е. выборка малая.
В случае повторного отбора найдем границы доверительного интервала для генерального среднего по формуле (5.5), считая σ ≈ s :
|
s |
|
|
s |
|
|
; |
x +tкр |
|
||
x −tкр |
n |
|
. |
||
|
|
|
n |
||
Найдем выборочное среднее арифметическое:
|
1 |
n |
1 |
|
||
x = |
∑xi = |
(125 +78 +102 +140 +90 + 45 +50 +125 +115 +112) = 98.2 |
||||
|
|
|
||||
|
n i=1 |
10 |
|
|||
и несмещенную оценку дисперсии
|
1 |
n |
1 |
((125 −98.2)2 |
|
|
s2 = |
∑(xi − x)2 = |
+(78 −98.2)2 + |
||||
|
9 |
|||||
|
n −1 i=1 |
|
|
|||
63
+(102 −98.2)2 +(140 −98.2)2 +(90 −98.2)2 +(45 −98.2)2 +
+(50 −98.2)2 +(125 −98.2)2 +(115 −98.2)2 +(112 −98.2)2 )=1033.29.
Тогда оценка среднего квадратического отклонения σ равна
s =  s2 =
s2 =  1033.29 = 32.14.
1033.29 = 32.14.
По таблице распределения Стьюдента (приложение 3) найдем значение tкр = t(k; α) для двусторонней критической области. Число степеней свободы
k здесь равно k = n −1 = 9, а вероятность α =1 − γ = 0.05. Тогда tкр = t(k; α)= 2.26 (двусторонняя область).
При повторном случайном отборе средняя ошибка выборки равна
σ ≈ |
s |
= 32.14 =10.16, |
а |
предельная |
ошибка |
n |
n |
10 |
|
|
|
ε = tкр |
σ |
= 2.26 10.16 = 22.97, |
т.е. |
доверительный интервал имеет гра- |
|
|
n |
|
|
|
|
ницы (x −ε; x +ε) = (98.2 −22.97; 98.2 + 22.97) = (75.63; 121.17).
При условии, что отбор квартир был повторным, с вероятностью 0.95 можно ожидать, что средний расход электроэнергии на одну квартиру во всем доме находится в интервале от 75.63 кВт ч до 121.17 кВт ч .
Найдем теперь границы доверительного интервала, считая отбор бесповторным. Предельную ошибку ε определим с учетом того, что генеральная
совокупность конечна и имеет объем N (табл. 5.1).
|
|
|
|
ε = tкр s 1 − n . |
|
|
|
|
|
|
|
n |
N |
|
|
Из |
условия |
задачи |
x = 98.2, |
s = 32.14, n =10, N = 70, |
γ = 0.95, |
||
tкр = tкр(9; 0.05) = 2.26. |
|
Отсюда |
предельная |
ошибка |
выборки |
||
ε = 2.26 |
32.14 |
1 − 10 |
= 21.27 и доверительный интервал имеет границы |
||||
|
10 |
70 |
|
|
|
|
|
(x −ε; x +ε) = (98.2 −21.27; 98.2 + 21.27) = (76.93; 119.47).
При условии, что отбор квартир был бесповторным, с вероятностью 0.95 можно утверждать, что средний расход электроэнергии на одну квартиру во всем доме находится в интервале от 76.93 кВт ч до 119.47 кВт ч.
Формула (5.3) позволяет при заданной доверительной вероятности γ и
требуемой точности ε определить объем выборки n, учитывая тип отбора данных.

64
Пример 4. С помощью случайного повторного отбора определяется средний стаж работы служащих фирмы. Предполагается, что он подчиняется нормальному закону распределения. Каким должен быть объем выборки, чтобы с доверительной вероятностью 0.95 можно было утверждать, что, принимая полученный средний стаж работы за истинный, совершается погрешность, не превышающая 0.5 года, если стандартное отклонение σ равно 2.7 года?
|
Решение. По условию ε = 0.5, σ = 2,7, γ = 0.95 и требуется найти объ- |
||||||||||
ём |
выборки |
n |
при повторном |
отборе. В |
этом случае 2Φ(uкр) = γ, где |
||||||
uкр |
= ε n . |
По таблице функции Лапласа (приложение 1) найдем, при каком |
|||||||||
|
σ |
|
|
γ |
|
|
|
|
|
|
|
uкр |
значение |
Φ(uкр) = |
= 0.475. Получим |
uкр =1.96. Отсюда необходи- |
|||||||
2 |
|||||||||||
мый объем выборки |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
σ 2 |
1.96 2.7 |
|
2 |
||
|
|
|
n = uкр |
|
= |
0.5 |
|
=112.02. |
|||
|
|
|
|
|
|
ε |
|
|
|
||
Учитывая, что необходимо не превышать заданную ошибку, округляем результат до большего целого: n =113.
Итак, чтобы с вероятностью 0.95 и точностью ε = 0.5 года определить средний стаж работы в фирме, требуется опросить не менее 113 служащих.
5.2.3. Интервальное оценивание генеральной доли (вероятности события)
Для определения вероятностей интересующих нас событий мы применяем выборочный метод: проводим n независимых экспериментов, в каждом из которых может произойти (или не произойти) событие А (вероятность р появления события А в каждом эксперименте постоянна). Тогда относительная
частота p появлений событий А в серии из n испытаний принимается в качестве точечной оценки для вероятности p появления события А в отдельном испытании. При этом величину p называют выборочной долей появлений
события А, а р — генеральной долей.
В силу следствия из центральной предельной теоремы (теорема МуавраЛапласа) относительную частоту события при большом объеме выборки мож-
но считать нормально распределенной с параметрами |
M ( p ) = p и |
|
σ( p ) = |
p(1 − p) . |
|
|
n |
|
Поэтому при n > 30 доверительный интервал для генеральной доли можно построить, используя формулы (5.2)–(5.4):
65
|
|
|
|
p |
|
(1 − p |
|
) |
|
|
|
|
p |
|
(1 |
− p |
|
|
|
|
p |
−uкр |
|
|
; |
p |
+uкр |
|
|
) |
(5.6) |
||||||||
|
|
|
|
n |
|
|
|
|
|
n |
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где uкр находится по таблицам функции Лапласа с учетом заданной довери-
тельной вероятности γ: 2Φ(uкр) = γ. |
|
|
|
||
При малом объеме выборки |
(n ≤ 30) |
предельная ошибка εопределяется по |
|||
таблице распределения Стьюдента |
|
|
|
||
ε = tкр |
p (1 − p ) |
, |
(5.7) |
||
n |
|||||
где tкр = t(k; α) и число |
|
|
k = (n −1), вероятность |
||
степеней |
свободы |
|
|||
α =1 − γ (двустороння область).
Формулы (5.6), (5.7) справедливы, если отбор проводился случайным повторным образом (генеральная совокупность бесконечна), в противном случае необходимо сделать поправку на бесповторность отбора (табл. 5.2).
Таблица 5.2
Средняя ошибка выборки для генеральной доли
Генеральная |
Бесконечная |
Конечная |
|
|
|
|
совокупность |
объема N |
|
|
|
||
|
|
|
|
|||
Тип отбора |
Повторный |
Бесповторный |
|
|||
Средняя ошибка выборки |
p (1 − p ) |
p (1 − p ) |
|
|
|
n |
|
|
1 |
− |
|||
|
n |
n |
N |
|||
|
|
|
|
|||
Пример 3. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет p = 900270 = 0.3 (относительная частота женщин среди всех опрошенных).
Так как отбор является повторным, и объем выборки велик (n = 900), предельная ошибка выборки определяется по формуле
ε = uкр |
p (1 |
− p ) |
. |
|
n |
||||
|
|
|||

66
Значение uкр находим по таблице функции Лапласа из соотношения
2Φ(uкр) = γ, т.е. |
Φ(uкр) = |
γ |
= |
0.95 |
= 0.475. Функция Лапласа (приложе- |
|
2 |
||||
|
2 |
|
uкр =1.96. Следовательно, предельная |
||
ние 1) принимает значение 0.475 |
при |
||||
ошибка ε =1.96 |
0.3(1 −0.3) = 0.18, и искомый доверительный интервал |
||||
|
900 |
|
|
|
|
( p −ε; |
p +ε) = (0.3 −0.18; 0.3 +0.18) = (0.12; 0.48). |
||||
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример 4. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. |
Выборочная доля «удачных» дней составляет |
p = |
24 = 0.6. |
||||
|
|
|
|
40 |
|||
По таблице функции Лапласа найдем |
значение uкр |
при |
заданной |
||||
доверительной |
вероятности γ = 0.98 : |
2Φ(uкр) = γ, Φ(uкр) = |
|
γ |
= 0.49, |
||
2 |
|||||||
|
|
|
|
|
|||
Φ(2.33) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
ε = uкр |
p (1 − p ) |
1 |
− |
n |
, |
|
n |
|
N |
||||
|
|
|
|
|
||
где n = 40, N = 365 (дней). Отсюда |
|
|
|
|
|
|
ε = 2.33 |
0.6(1 −0.6) |
|
1 − |
40 |
= 0.17 |
|
|
40 |
|
|
365 |
|
|
и доверительный интервал для генеральной доли
( p −ε; p +ε) = (0.6 −0.17; 0.6 +0.17) = (0.43; 0.77).
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
67
6.ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
6.1.Постановка задачи
Вобычной речи слово «гипотеза» означает предположение. В статистике
—это предположение о виде закона распределения («данная генеральная совокупность нормально распределена»), о значениях его параметров («генеральное среднее равно нулю»), об однородности данных («эти две выборки извлечены из одной генеральной совокупности»). Статистическая проверка гипотезы состоит в выяснении того, согласуются ли результаты наблюдений (выборочные данные) с нашим предположением.
Результатом такой проверки может быть отрицательный ответ: выборочные данные противоречат высказанной гипотезе, поэтому от нее следует отказаться. В противном случае мы получаем ответ неотрицательный: выборочные данные не противоречат гипотезе, поэтому её можно принять в качестве одного из допустимых решений (но не единственно верного).
Статистическая гипотеза, которая проверяется, называется основной (ну-
левой) и обозначается H0. Гипотеза, которая противопоставляется основной, называется альтернативной (конкурирующей) и обозначается H1. Цель ста-
тистической проверки гипотез: на основании выборочных данных принять решение о справедливости основной гипотезы или отклонить в ее пользу альтернативной.
Так как проверка осуществляется на основании выборки, а не всей генеральной совокупности, то существует вероятность, возможно, очень малая, ошибочного заключения.
Так, нулевая гипотеза может быть отвергнута, в то время как в действительности в генеральной совокупности она является справедливой. Такую ошибку называют ошибкой первого рода, а её вероятность — уровнем значи-
мости и обозначают α. Возможно, что нулевая гипотеза принимается, в то время как в генеральной совокупности справедлива альтернативная гипотеза. Такую ошибку называют ошибкой второго рода, а её вероятность обозначают
β (табл. 6.1).
Таблица 6.1
Результаты проверки статистической гипотезы
Принятое |
В генеральной совокупности гипотеза H0 |
|||||
решение |
|
|
|
|
|
|
|
Верна |
Неверна |
||||
H0 отвергнута |
Ошибка 1 рода |
Правильное решение |
||||
|
P(H1 |
H0 ) = α |
P(H1 |
H1) =1 −β |
||
|
|
|
||||
H0 принята |
Правильное решение |
Ошибка 2 рода |
||||
|
P(H0 |
H0 ) =1 −α |
P(H0 |
H1) =β |
||
|
|
|
|
|
|
|
68
Проверка статистических гипотез осуществляется с помощью статистического критерия. Статистический критерий K — это правило (функция от результатов наблюдений), определяющее меру расхождения результатов наблюдений с нулевой гипотезой. Вероятность 1 −β называют мощностью
критерия.
При проверке статистических гипотез принято задавать заранее уровень значимости α (стандартные значения: 0.1, 0.05, 0.01, 0.001). Тогда из двух критериев, характеризующихся одной и той же вероятностью α, выбирают
тот, которому соответствует меньшая ошибка 2-го рода, т.е. большая мощность. Уменьшить вероятности обеих ошибок αи β одновременно можно,
увеличив объем выборки.
Значения критерия K разделяются на две части: область допустимых значений (область принятия гипотезы H0 ) и критическую область (область
принятия гипотезы H1 ). Критическая область состоит из тех же значений критерия К, которые маловероятны при справедливости гипотезы H0 . Если значение Kнабл критерия K, рассчитанное по выборочным данным, попадает в критическую область, то гипотеза H0 отвергается в пользу альтернативной H1; в противном случае мы утверждаем, что нет оснований отклонять гипоте-
зу H0 .
Пример. Для подготовки к зачету преподаватель сформулировал 100 вопросов (генеральная совокупность) и считает, что студенту можно поставить «зачтено», если тот знает 60 % вопросов (критерий). Преподаватель задает студенту 5 вопросов (выборка из генеральной совокупности) и ставит «зачте-
но», если правильных ответов не меньше трех. Гипотеза H0 : «студент курс усвоил», а множество {3, 4, 5} — область принятия этой гипотезы. Критической областью является множество {0,1, 2}— правильных ответов меньше трех, в этом случае основная гипотеза отвергается в пользу альтернативной H1 : «студент курс не усвоил, знает меньше 60 % вопросов».
Студент А выучил 70 вопросов из 100, но ответил правильно только на два из пяти, предложенных преподавателем, — зачет не сдан. В этом случае преподаватель совершает ошибку первого рода.
Студент Б выучил 50 вопросов из 100, но ему повезло, и он ответил правильно на 3 вопроса — зачет сдан, но совершена ошибка второго рода.
Преподаватель может уменьшить вероятность этих ошибок, увеличив количество задаваемых на зачете вопросов.
Чтобы построить критическую область, нужно знать закон распределения статистики K при условии, что гипотеза H0 справедлива. Уровень зна-
чимости α (вероятность наблюдаемому значению попасть в крити-
69
ческую область) определяет «размер» критической области, а конкурирующая гипотеза H1 — «форму» критической области. Например, если проверяется
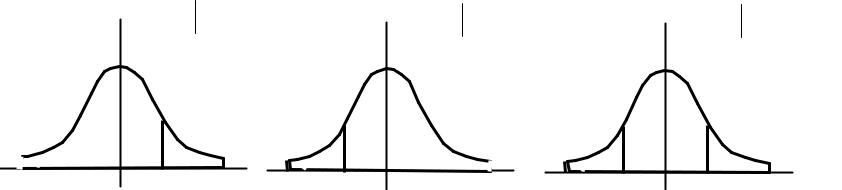
гипотеза H0 : θ = θ0 , а в качестве альтернативы — H1 : θ > θ0 , то критическая область будет правосторонней (рис. 6.1, а). При альтернативе H1 : θ < θ0 критическая область — левосторонняя (рис. 6.1, б). При альтернативе H1 : θ = θ0 критическая область — двусторонняя (рис. 6.1, в). Во всех этих случаях при заданном уровне значимости α заштрихованная площадь составляет 100 α % от всей площади под кривой плотности распределения статистики K.
|
fK (x H0 ) |
|
0 |
Kкр |
x |
а |
|
|
|
|
fK (x H0 ) |
−Kкр |
0 |
x |
|
б |
|
|
|
fK (x H0 ) |
|
−Kкр |
0 |
Kкр |
x |
|
|
в |
|
Рис. 6.1. Правосторонняя (а), левосторонняя (б) и двусторонняя (в) критические области
Алгоритм проверки статистических гипотез сводится к следующему:
1)сформулировать основную H0 и альтернативную H1 гипотезы;
2)выбрать уровень значимости α;
3)в соответствии с видом гипотезы H0 выбрать статистический крите-
рий для ее проверки, т.е. случайную величину K, распределение которой известно;
4) по таблицам распределения случайной величины K найти границу критической области Kкр (вид критической области определить по виду аль-
тернативной гипотезы H1 );
5)по выборочным данным вычислить наблюдаемое значение критерия
Kнабл;
6)принять статистическое решение: если Kнабл попадает в критиче-
скую область — отклонить гипотезу H0 в пользу альтернативной H1 ; если Kнабл попадает в область допустимых значений, то нет оснований отклонять основную гипотезу.

70
6.2. Проверка гипотез о параметрах распределения
6.2.1. Гипотезы о значениях генерального среднего и дисперсии
Рассмотрим нормальную генеральную совокупность X ~ N (a, σ), параметр a которой требуется определить по выборочным данным. Например, задан требуемый номинальный размер a0 деталей, вытачиваемых на данном
станке. Отобрав из всей продукции выборку объема n, определить по ней, соответствует ли производимая продукция заданному требованию. В этом случае
речь идет о проверке гипотезы H0 : a = a0 о равенстве генерального среднего a заданному значению a0 . Для проверки этой гипотезы используются
статистики, распределение которых известно (табл. 6.2). По выборке вычисляются оценки неизвестных параметров распределения:
|
|
|
|
|
1 |
n |
|
|
|
|
a = x |
= |
|
∑xi ; |
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
n i=1 |
|
|
||
|
|
|
1 |
|
|
|
n |
|
|
|
σ2 = s2 = |
|
|
|
∑(xi − x)2. |
|
|||
|
|
|
|
|
|
||||
|
|
n −1 i=1 |
|
Таблица 6.2 |
|||||
|
Гипотеза о генеральном среднем |
||||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Гипотеза |
|
|
|
|
|
|
H : a = a0 |
|
|
Предположения |
Генеральная совокупность |
Генеральная совокупность |
|||||||
|
нормальна; параметр σ |
нормальна; параметр σ |
|||||||
|
известен |
|
|
|
|
неизвестен |
|||
Оценки |
|
|
|
|
|
|
|
|
|
по выборке |
a = x |
|
|
|
|
|
a = x; |
σ = s |
|
Статистика K |
X −a0 |
|
|
n |
X −a0 n |
||||
|
|
||||||||
|
σ |
|
|
|
|
|
|
s |
|
Распределение |
Стандартное нормальное |
Распределение Стьюдента |
|||||||
статистики K |
N (0,1) |
|
|
|
|
T(n−1) |
|||
Эти же статистики используются, если распределение генеральной совокупности неизвестно (для выборок объема n > 30 используется статистика с нормальным распределением, для n ≤ 30 с распределением Стьюдента).
Пример 1. Техническая норма предусматривает в среднем 40 с на выполнение определенной технологической операции на конвейере по производству часов. От работающих поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки жалобы проведены
