Шпаргалка высшая математика

Неопределенный интеграл

1. Функция F(x) называется первообразной

для функции f(x) (дифференциала f(x) dx) на отрезке [a,b],

если F(x) дифференцируема на [a,b] и F’(x) =f(x) для

всех x принадлежащих [a,b] ( dF(x) =f(x)dx ).

2. Если F(x) — первообразная для

функции f(x), то F(x) +C, где C — некоторая константа,

также является первообразной для f(x).

Доказательство. Действительно, (F(x) + C)’ =F’(x) + C’ =f(x).

Теорема доказана.

3. Множество всех первообразных функции f(x)

(дифференциала f(x) dx) называется неопределенным ин-

тегралом от этой функции и обозначается .

4. Укажем несколько свойств неопределенного интеграла.

1. d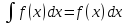

Действительно, если F(x) —какая-либо первообразная функ-

ции f(x), то d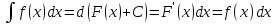

2.

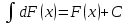
Доказывается аналогично.

3. =

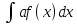Вычисляя дифференциал правой части, получаем

d (a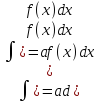 . Последнее означает спра-

ведливость доказываемого свойства.

4. .

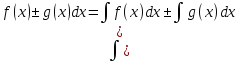Аналогично предыдущему, вычисляя дифференциал правой

части, получаем

d(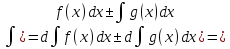 f(x)dx 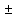g(x)dx = (f(x) 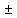g(x))dx =d (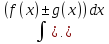Свойство доказано.

Заметим, что свойства 3 и 4 означают линейность операции

интегрирования.

5.

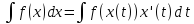
Так как по свойству инвариантности формы первого диффе-

ренциала, f(x)dx = f(x(t)) x’(t) dt , то, используя свойство 1, полу-

чаем

d .

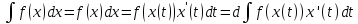Утверждение доказано. Это свойство лежит в основе нахож-

дения интеграла с помощью замены переменной.

Используя свойства 1–5 и свойства дифференциалов, сводят

вычисление интегралов к так называемым табличным интег-

ралам.

5.

6.  К специальным функциям относятся и многие первообразные для элементарных функций, причём часто не столь уж "сложной" структуры. Интегралы, выражающиеся через такие первообразные, называются (по традиции, берущей начало в 18 веке) неберущимися. Итак, интеграл  не берётся, если функция  не является элементарной.

7. Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием. 

Иногда удается представить подынтегральное выражение

f(x) dx в виде 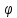(u) du, где u — некоторая функция от x, то

есть записать его в форме f(x)dx =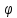(u(x))du(x) , и при этом

интеграл 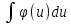является табличным. Тогда если 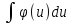= F(u) +C , то по свойству 5 неопределённого интеграла

F(u(x)) +C =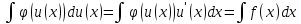

Этот прием называется подведением под знак дифференциала и представляет собой простейший вариант использования

формулы замены переменной, выраженной свойством 5.

8. Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

называемое формулой интегрирования по частям. Понимают его

в том смысле, что множество первообразных, стоящее в

левой части, совпадает со множеством первообразных, получаемых по правой части.

9. Пусть требуется найти интеграл  , где функция  непрерывна на некотором интервале  . Сделаем замену переменной в подынтегральном выражении, положив  , где  - функция непрерывно дифференцируемая на некотором интервале T и имеющая обратную функцию

 (1)

определенную на  . Так как , получим

 (2)

то есть, вычисление исходного интеграла  сводится к вычислению

интеграла  , стоящего в правой части равенства (2.). По окончании вычислений необходимо вернуться к переменной  , пользуясь равенством (1).

Замечание 1.Часто целесообразно подобрать замену переменной не в виде  , а в виде  .

10.