Методы проецирования.
Центральное проецирование – Общий случай проецирования геометрических образов из центра на плоскость.
Параллельное проецирование - Частный случай центрального проецирования с бесконечно удаленным центром проекций. Осуществляется оно пучком параллельных проецирующих лучей заданного направления.
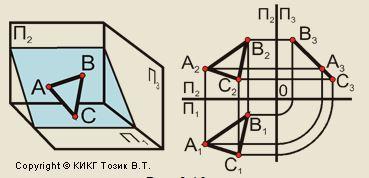
Метод Монжа – Метод параллельного проецирования, при котором берутся прямоугольные (ортогональные) проекции на две взаимно перпендикулярные плоскости проекций.
2. Комплексный чертеж - это совокупность двух или более взаимосвязанных ортогональных проекций геометрической фигуры, расположенной на одной плоскости чертежа.
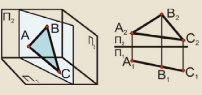
3. Прямая общего положения.
Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций, пересекает все 3 плоскости.
Прямые частного положения.
Прямые частного положения - это прямые, параллельные одной или двум плоскостям проекций.
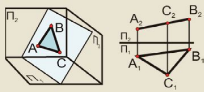
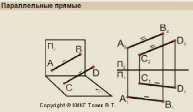
4. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.
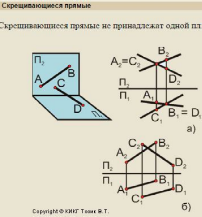
Скрещивающимися называются две прямые не лежащие в одной плоскости.
5. Прямая уровня – прямая, параллельная какой-либо из плоскостей проекций.
Горизонталь - Параллельна горизонтальной плоскости проекций (ZA=ZB)
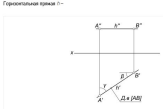
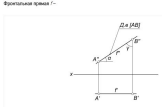
Фронталь – Параллельна фронтальной плоскости проекций (YA=YB)
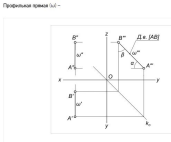
Профильная прямая – Параллельна профильной плоскости проекций (XA=XB)
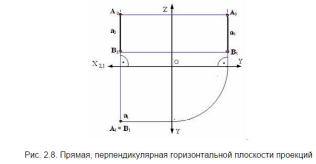
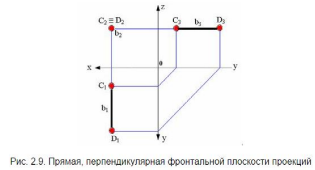
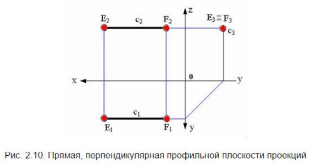
6. Проецирующая прямая - Прямая, перпендикулярная какой-либо плоскости проекций.
7. Метод прямоугольного треугольника.
Метод прямоугольного треугольника служит для определения величины отрезка и его углового наклона к плоскостям проекций. - Первый катет этого треугольника равен проекции отрезка на плоскости проекций;
- Из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
- Гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
- Угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
8. Параллельные прямые
Пересекающиеся прямые
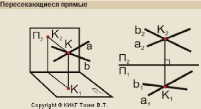
Скрещивающиеся прямые
9. Способ вращения. Способ вращения заключается в том, что отрезок прямой линии или плоскую фигуру вращают вокруг выбранной оси до положения, параллельного плоскости проекций.
10. Сущность метода замены плоскостей проекций состоит в том, что предмет остается неподвижен, а плоскости проекций принимают положение, удобное для решения задачи.
11.
Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии
2. прямой линией и точкой, не принадлежащей этой прямой
3. двумя пересекающимися прямыми
4. двумя параллельными прямыми
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Биссекторной плоскостью двугранного угла называют плоскость, которая делит этот
угол на два равных двугранных угла. Биссекторная плоскость проходит через ребро
двугранного угла и точку на биссектрисе любого линейного угла, не лежащую на ребре
12. Плоскость общего положения
Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0° и 90°) называется плоскостью общего положения
Плоскость частного положения — плоскость, которой принадлежат проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Именно поэтому ее иногда называют проецирующей плоскостью. Существует три вида проецирующих плоскостей:
|
|
На (рис. 2.19,а) представлена горизонтально-проецирующая плоскость, т.е. перпендикулярная к П1. И поэтому она проецируется на П1 в виде прямой линии |
|
|
На (рис. 2.19,б) представлена фронтально-проецирующая плоскость, т.е. перпендикулярная к П2. И поэтому она проецируется на П2 в виде прямой линии. |
|
|
На (рис. 2.19,в) представлена профильно-проецирующая плоскость, т.е. перпендикулярная к П3. И поэтому она проецируется на П3 в виде прямой линии. |
13.
14. Пересечение прямой с плоскостью общего положения. Пример 1. Даны: плоскость общего положения а и прямая общего положения АВ (А1В1 А2В2); требуется найти точку их пересечения (фиг.251,а). Проводим через прямую АВ какую - либо вспомогательную плоскость, например горизонтально - проектирующую плоскость δ (δ1), как показано на (фиг.251,б); она пересечет плоскость a по прямой NM (N1M1, N2М2), которая, в свою очередь, пересечет прямую АВ (А1В1 А2В2) в точке С(С1С2), что видно на (фиг.251,в). Точка С есть точка пересечения прямой АВс плоскостью а.
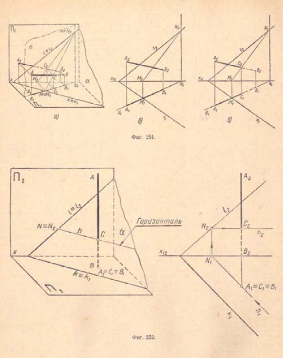
Пример
2. На
(фиг.252)
приведен пример нахождения проекций
точки пересечения прямой AB c
плоскостью общего положения при помощи
горизонтали h.
Пример
3. Даны:
треугольник ABC и
прямая NM;
требуется определить точку их пересечения
(фиг.253,а).
Возьмем
в качестве вспомогательной плоскости
горизонтально - проектирующую плоскость δ,
тогда горизонтальная проекция ог
сольется с горизонтальной
проекцией N1M1 прямой NM и
пересечет проекции сторон треугольника
в точках Е1 и F1 (фиг.253,б).
Отрезок Е1F1 будет
горизонтальной проекцией линии
пересечения. Затем находим фронтальную
проекцию линии пересечения: при помощи
вертикальных линий связи получаем
точки Е2 и F2,
проводим через них прямую E2F2,
которая будет фронтальной проекцией
линии пересечения.
Прямая E2F2 пересекает
прямую N2М2 в
точке К2.
Точка К2 будет
фронтальной проекцией точки пересечения
прямой MN с
прямой EF;
горизонтальную проекцию K1 этой
точки определяем при помощи вертикальной
линии связи.
Точка
К (K1,
К2)
будет точкой пересечения данной
прямой MN с
данным треугольником ABC,
как одновременно им принадлежащая,
потому что прямая MN пересекается
в ней с прямой EF,
лежащей в плоскости треугольника ABC.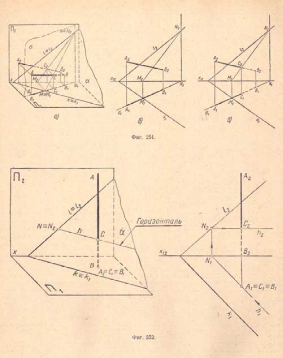
15. Точка принадлежит поверхности, если она принадлежит какой-либо линии на этой поверхности. Для построения точек на поверхности или определения недостающих проекций строится сечение поверхности вспомогательной плоскостью. Вспомогательная плоскость выбирается таким образом, чтобы в сечении получались простые линии – прямые или окружности. Кроме того, окружность в сечении должна проецироваться на одну из плоскостей проекций без искажения.
16.
17.
18.
Инженерная графика
19. Вид- изображение обращенной к наблюдателю видимой части поверхности предмета. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета при помощи штриховых линий.
|
Устанавливаются следующие названия видов, получаемых на основных плоскостях проекций: |
1- вид спереди (главный вид);
2- вид сверху;
3- вид слева;
4- вид справа;
5- вид снизу;
6- вид сзади.
Главный вид должен содержать наибольшую информацию о предмете.
Если местный вид располагается в проекционной связи с одним из основных видов (рис. 85, а), то он не обозначается. Если местный вид расположен не в проекционной связи с одним из основных видов, то он обозначается стрелкой и буквой русского алфавита
20. Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций
Дополнительный вид должен быть отмечен на чертеже прописной буквой ,а у связанного с дополнительным видом изображения предмета должна быть поставлена стрелка, указывающая направление взгляда, с соответствующим буквенным обозначением.
Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим изображением, стрелку и обозначение вида не наносят
21. Изображение отдельного, ограниченного места поверхности предмета называется местным видом . Местный вид может быть ограничен линией обрыва, по возможности в наименьшем размере, или не ограничен. Местный вид должен быть отмечен на чертеже подобно дополнительному виду.
22. Сечение - изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями (рис. 18). На сечении показывается только то, что получается непосредственно в секущей плоскости.
Вынесенные сечения являются предпочтительными и их допускается располагать в разрыве между частями одного и того же вида
Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями, а контур наложенного сечения – сплошными тонкими линиями, причем контур изображения в месте расположения наложенного сечения не прерывают.
Ось симметрии вынесенного или наложенного сечения указывают штрих - пунктирной тонкой линией без обозначения буквами и стрелками и линию сечения не проводят