3.2. Конечные автоматы

Конечным автоматом называется пятерка

A= (Q,q₀,F),

где Q= {q₀,q₂, …,q_n}– конечное множество состояний устройства управления;

{a₁,a₂, …,a_k} – конечный входной алфавит;

 – функция переходов, отображающая Qво множество подмножеств множестваQ;

q₀ – начальное состояние устройства управления;

F– множество заключительных состояний, причемFQ.

Конечный автомат можно представить себе следующим образом. На бесконечной ленте с ячейками записана входная цепочка символов ^*; управляющее устройство с читающей головкой движется слева направо и считывает символы с ленты. После перехода к новой ячейке, управляющее устройство попадает в новое состояние, определяемое функцией переходов. На рисунке изображен автомат в начальном состоянии, считывающий первый символ входной цепочки {a_s1,a_s2, … ,a_sp}.

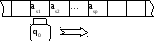
Конфигурацией конечного автомата называется пара (q,), гдеqQ– состояние устройства управления, а^*– неиспользованная часть входной цепочки. Такт автомата определяется на конфигурациях. Например, если(q₁,a) содержитq₂, то, выполнив такт, автомат перейдет от конфигурации (q₁,a) к конфигурации (q₂,). Используя бинарное отношение, обозначаемое символом├, указанный выше такт можно записать следующим образом:

(q₁,a)├ (q₂,).

Это говорит о том, что если конечный автомат находится в состоянииq₁ и входная головка обозревает входной символа, то автомат может делать такт, за который он переходит в состояние,q₂ и сдвигает головку на одну ячейку вправо.

Входная цепочка допускается автоматом, если найдется последовательность тактов, переводящая автомат из начальной конфигурации (q₀,) в заключительную (q_f,), здесьq_f – некоторое заключительное состояние,пустая цепочка.

Конечный автомат называется детерминированным, если множество (q,a) содержит не более одного состояния для любыхqQиaЕсли множество(q,a) содержит более одного состояния, то автомат называется недетерминированным.Единственное отличие недетерминированного конечного автомата от детерминированного заключается в том, что значениями функции переходов являются не состояния, а множества состояний (или,в терминах команд, возможны различные команды с одинаковыми левыми частями). Это соответствует тому факту, что в диаграмме состояний из одной вершины может исходить несколько дуг с оди­наковой пометкой.

Рассмотрим конечный детерминированный автомат А1, допускающий все цепочки из символов 0 и 1, которые начинаются и оканчиваются 1. А1=({p,q,r}, {0, 1},,p, {r}), гдезадается следующей таблицей.


Состояние	Вход
	0	1
p	-	{q}
q	{q}	{r}
r	{q}	{r}

Функцию переходов можно задать с помощью диаграммы.

Функцию переходов можно задать с помощью команд:

(p, 1) =q;(q, 0) =q;(q, 1) =r;(r, 0) =q;(r, 1) =r.

Для входа 1001 единственно возможной последовательностью конфигураций, начинающейся конфигурацией (p, 1001), будет

(p, 1001)├ (q, 001)

├ (q, 01)

├ (q, 1)

├ (r,)

Таким образом 1001 допускается автоматом А1.

Рассмотрим конечный недетерминированный автомат А2, допускающий все цепочки из символов 0 и 1, которые оканчиваются цепочкой 010. А1=({s1,s2,s3,s4}, {0, 1},,s1, {s4}), гдезадается следующей диаграммой.


Состояние	Вход
	0	1
s1	{s1, s2}	{s1}
s2	-	{s3}
s3	{s4}	-
s4	-	-

Функцию переходов можно задать с помощью таблицы.

Эквивалентность языков, определяемых праволинейной грамматикой и конечным автоматом.

Рассмотрим теперь произвольную автоматную грамматику G = (N, , P, S) с правосторонними продукциями:

C → xB, или C → x, где C, B  N, x *.

Построим для нее недетерминированный конечный автомат

A = (Q,q₀,F),

где алфавиты в грамматике и автомате совпадают;Q=N{D}, причем символD не должен содер­жаться в N, q₀=S,F= {D}, аопределяется следующим образом:

1. каждой продукции вида C → xставится в соответствие команда(C,x) =D;

2. каждой продукции вида C → xBставится в соответствие команда(C,x) =B;

3. других команд нет.

Ввиду того, что любой регулярный язык может быть порожден автоматной грамматикой с правосторонними продукциями, можно ограничиться рассмотрением именно таких грамматик.

Пример. Пусть грамматикаG = (N, , P, S) задается следующим образом:

N= {S,L}, = {a,b, 0, 1},

P= {S→aL,S→bL,S→a,S→b,L→aL,L→bL,

L→0L,L→1L,L→a,L→b,L→0,L→1}.

Построим для нее конечный автомат

A = (Q,q₀,F),

 = {a,b, 0, 1},Q= {S,L}{D},q₀=S,F= {D},

(S, a) = L; (S, b) = L; (S, a) = D; (S, b) = D; (L, a) = L; (L, b) = L;

(L, 0) = L; (L, 1) = L; (L, a) = D; (L, b) = D; (L, 0) = D; (L, 1) = D;

Теперь рассмотрим произвольный недетерминированный конеч­ный автомат

A = (Q,q₀,F).

Такому автомату можно поставить в соответствие следующую автоматную грамматику:

G = (N, , P, S),

где алфавиты в грамматике и автомате совпадают;N =Q,S = q₀, а множествоР строится следую­щим образом:

1. каждой команде автомата (q_i, a_j ) = q_k ставится в соответствие продукцияq_i→ a_jq_k, еслиq_i,q_k Q,a_j;

2. каждой команде (q_i, a_j ) = q_k ставится в соответствие еще одна продукцияq_i→ a_j, еслиq_k F;

3. других продукций нет.

Рассмотрим конечный детерминированный автомат А1, допускающий все цепочки из символов 0 и 1, которые начинаются и оканчиваются 1. А1=({p,q,r}, {0, 1},,p, {r}), гдезадается следующими командами:

(p, 1) =q;(q, 0) =q;(q, 1) =r;(r, 0) =q;(r, 1) =r;

этому автомату поставим в соответствие следующую автоматную грамматику

G = (N, , P, S),

 ={0, 1}, N ={p, q, r}, S = p,

P = {p→ 1q; q→ 0q; q→ 1r; q→ 1; r→ 0q; r→ 1r; r→ 1 }