1.1.8. Решение задач 1-3 контрольной работы № 1

Задача 1. Решить задачу, пользуясь диаграммой Эйлера-Венна.

Группа туристов из 100 человек пробыла в городе Nтри дня. За это время драматический театр посетили 28 туристов, оперный – 42, кукольный – 30. И в драматическом, и в оперном побывало 10 человек; в драматическом и кукольном – 8; в оперном и кукольном – 5. Все три театра посетили три человека. Сколько туристов не были ни в одном театре?

Решение.В задаче идет речь о трех множествахД,О,К– зрителей драмы, оперы и кукольного спектакля соответственно. Универсальное множествоU– это множество туристов группы. Используя обозначение– количество элементов множестваХ, запишем кратко условие задачи:

U

В задаче требуется найти .

П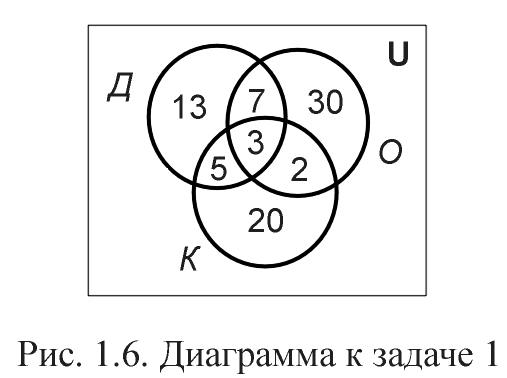еренесем эти данные на диаграмму Эйлера-Венна. Разметку диаграммы начинаем с множества– здесь три элемента. В множестве-10 элементов, но три из них уже учтены. Оставшиеся 7 элементов проставляем на диаграмме и т.д.

Теперь на диаграмме (рис. 1.6) все элементы учтены ровно по одному разу, следовательно, количество туристов, которые побывали хотя бы в одном театре, равно

Количество туристов, не побывавших ни в одном театре

U

Ответ: не были ни в одном театре 20 человек.

Задача 2.Задано универсальное множествоUи множества.Перечислить элементы множества. Записать булеан множестваХ, какое-либо разбиение множестваY, покрытие множестваZ.

Решение.Для нахождения множестваWвыполним операции над множествами в следующем порядке:

1) 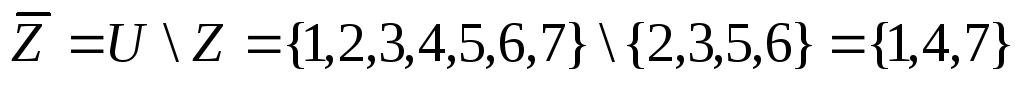- по определению операции дополнения;

2) - по определению операции пере-сечения множеств;

3) .

Итак,

Для построения булеана множества Xвоспользуемся двоичной записью числа. Если множествоXсодержитnэлементов, его булеан содержитподмножеств – в нашем случае 8 подмножеств. Будем записывать номер подмножества трехразрядным двоичным числом от 0 до 7, включая в подмножество только те элементы, которым соответствует единица в двоичном разряде (табл. 1.2).

Таблица 1.2

Булеан множества X

Номер подмножества	Двоичная запись номера	Подмножества множества
0	000	{} = 
1	001	{ 7}
2	010	{ 4 }
3	011	{ 4,7}
4	100	{2 }
5	101	{2, 7}
6	110	{2,4 }
7	111	{2,4,7}

Итак, в булеан множества Хвключаем пустое множество, само множествоХ, все одноэлементные подмножества, все двухэлементные подмножества множестваХ:

B,.

Для множества Y построим разбиение, состоящее из трех блоковR, например, таким образом:

Определение разбиения выполняется: множества не пусты, не пересекаются (, , ), их объединение равно множествуY:

Для построения покрытия выберем подмножества и . Полученная система множествPсостоит из двух блоков, объединение которых равно множествуZ:

.

Задача 3. Упростить выражение, пользуясь законами алгебры множеств:

.

Решение.Договоримся считать, что операция пересечения множеств имеет более высокий приоритет, чем объединение множеств, т.е., если нет скобок, изменяющих приоритет, вначале выполняется пересечение, а затем объединение. Пользуясь этим правилом и законом ассоциативности, определим порядок действий:

.

Выполним преобразования, указывая номер закона (табл. 1.1) над знаком равенства:

1. ;

2. ;

3. 

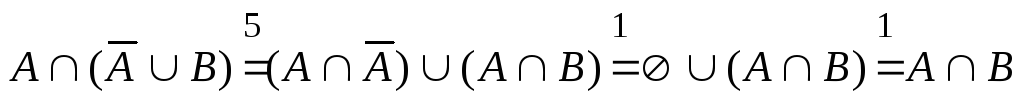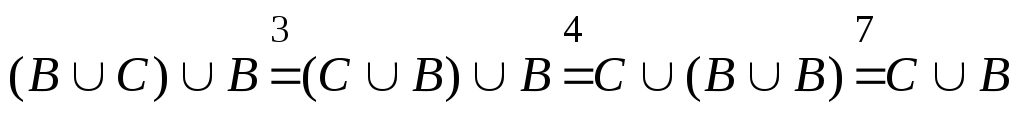Ответ:.

Задача 4контрольной работы 1 выполняется аналогично доказательству закона дистрибутивности (1.1) в подразделе 1.1.7.