
- •1.1.1. Понятие множества
- •1.1.2. Способы задания множеств
- •1.1.3. Основные определения
- •1.1.4. Диаграммы Эйлера – Венна
- •1.1.5. Операции над множествами
- •1.1.6. Системы множеств
- •1.1.7. Законы алгебры множеств
- •1.1.8. Решение задач 1-3 контрольной работы № 1
- •1.1.9. Контрольные вопросы и упражнения
- •1.2.1. Декартово произведение множеств. Соответствие множеств
- •1.2.2. Определение бинарного отношения
- •1.2.3. Способы задания бинарного отношения
- •1.2.4. Свойства бинарных отношений
- •1.2.5. Отношения эквивалентности
- •1.2.6. Отношения порядка
- •1.2.7. Частично упорядоченные множества
- •1.2.8. Диаграммы Хассе
- •1.2.9. Изоморфизм частично упорядоченных множеств
- •1.2.10. Решение задач 5,6 контрольной работы № 1
- •1.2.11. Контрольные вопросы и упражнения
- •1.3 Реляционная алгебра
- •1.3.1. Применение отношений для обработки данных
- •1.3.2. Теоретико-множественные операции реляционной алгебры
- •1.3.3. Специальные операции реляционной алгебры
- •1.3.4. Решение задачи 7 контрольной работы № 1
- •1.4. Конечные и бесконечные множества
- •1.4.1. Равномощные множества
- •1.4.2. Классы равномощных множеств
- •1.4.3. Сравнение множеств по мощности
- •1.4.4. Свойства конечных множеств
- •A b c
- •1.4.5. Определение счетного множества
- •1.4.6. Свойства счетных множеств
- •1.4.7. Несчетные множества
- •1.4.8. Булеан бесконечного множества. Выводы
- •1.4.9. Решение задач 8,9 контрольной работы 1
- •1.4.10. Контрольные вопросы и упражнения
++1. ТЕОРИЯ МНОЖЕСТВ
Множества и операции над ними
1.1.1. Понятие множества
Теория множеств опирается на три первичных понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого
определения этим понятиям не дается,
описывается только их применение. Для
этих понятий используются обозначения:
“![]() ”-
элементапринадлежит множествуА;
“
”-
элементапринадлежит множествуА;
“![]() ”элементсне принадлежит множествуА.
”элементсне принадлежит множествуА.
Говоря о некотором множестве, мы требуем его:
1) целостности, т.е. возможности рассматривать его как отдельный объект;
2) различимости его элементов;
3) неупорядоченности элементов.
Поэтому
записи
![]() и
и![]() определяют
одно и то же множество.
определяют
одно и то же множество.
1.1.2. Способы задания множеств
Множество можно задать, перечислив все
его элементы:
![]() ,
,
![]() . Порядок записи элементов множества
произволен. Часто задают множество,
указав его характеристическое свойство,
которое для каждого элемента позволяет
выяснить, принадлежит он множеству или
нет.
. Порядок записи элементов множества
произволен. Часто задают множество,
указав его характеристическое свойство,
которое для каждого элемента позволяет
выяснить, принадлежит он множеству или
нет.
Например,
![]() – целый корень уравнения
– целый корень уравнения![]() ,
,
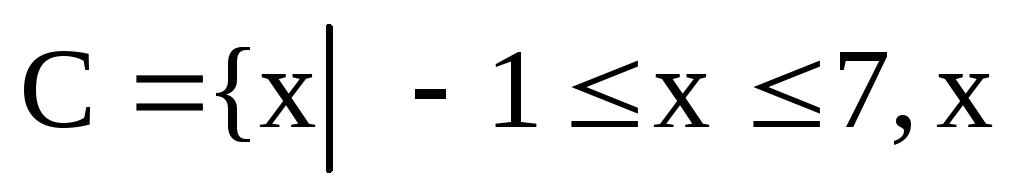 –
целое}.
–
целое}.
В дальнейшем для известных числовых множеств будут использоваться обозначения:
= { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых чисел;
Q– множество рациональных чисел;
R – множество действительных чисел.
1.1.3. Основные определения
Пустым множеством называется
множество,
не содержащее ни одного элемента, т.е.
для любого элементаxвыполняется![]() .
.
Универсальным называется множествоUвсех элементов, рассматриваемых в данной задаче.
Пример.ПустьU=Zи требуется найти все решения уравнения
![]() .
МножествоМрешений этой задачи
есть пустое множество:М=
.
.
МножествоМрешений этой задачи
есть пустое множество:М=
.
Пусть теперь U=R.
Тогда множествоМрешений
уравнения![]() не пусто:М =
не пусто:М =
![]() .
.
Будем говорить, что множество Авключается во множествоВ
![]() ,
если каждый элемент множестваАявляется элементом множестваВ( говорят также, чтоАявляется подмножеством множестваВ).
Из определения включения следуют
свойства:
,
если каждый элемент множестваАявляется элементом множестваВ( говорят также, чтоАявляется подмножеством множестваВ).
Из определения включения следуют
свойства:
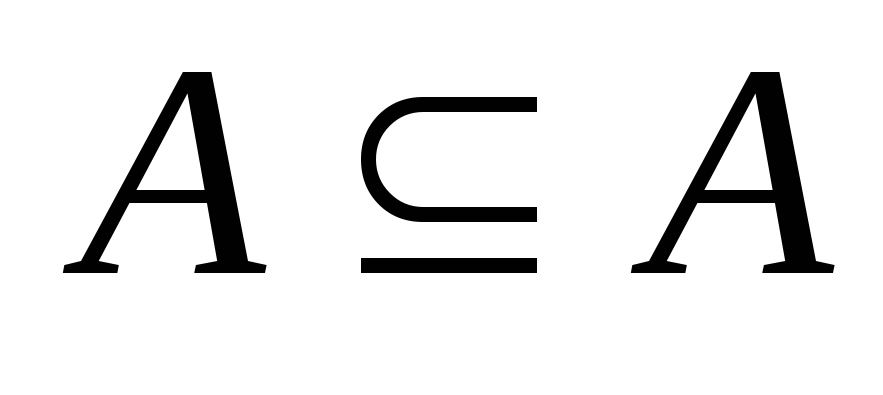 для любого множестваА;
для любого множестваА;Если
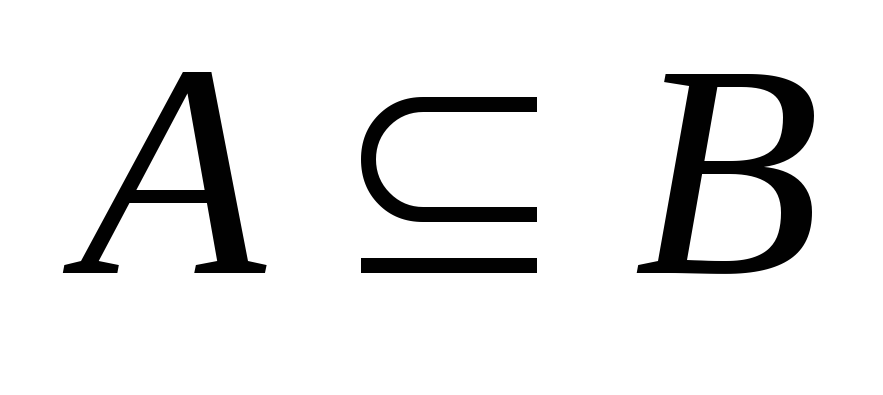 и
и
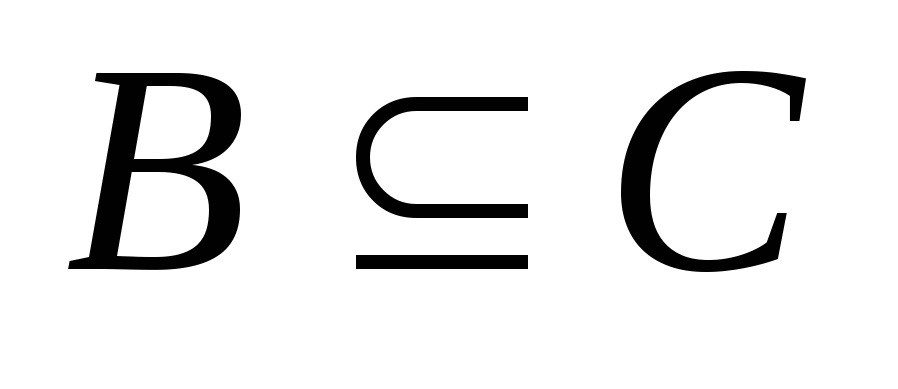 ,
то
,
то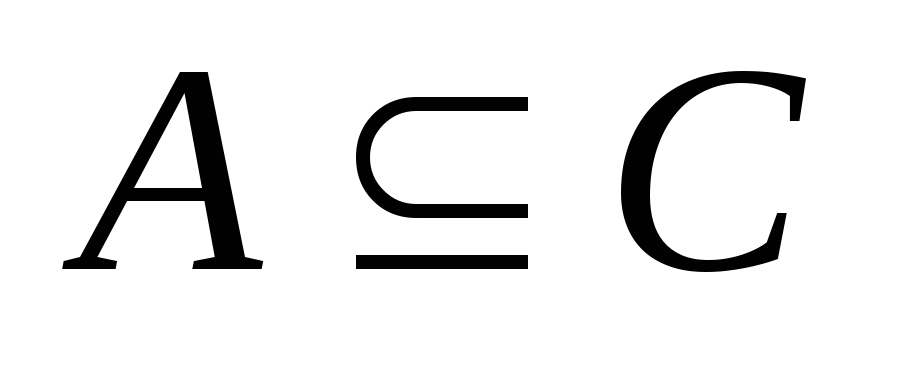 ;
;
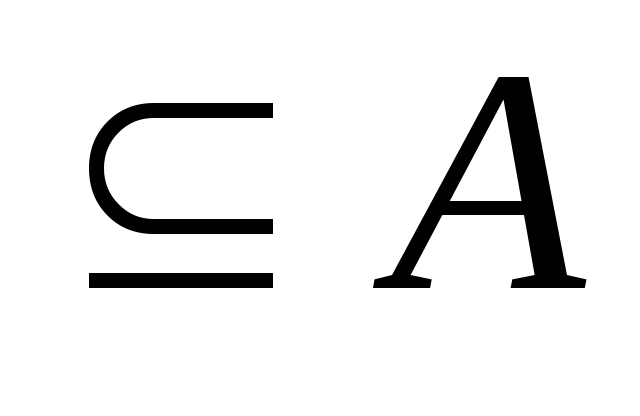 для любого множестваА;
для любого множестваА;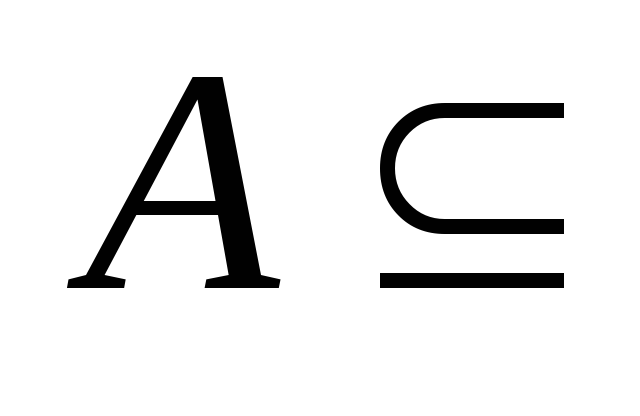 Uдля любого множестваА.
Uдля любого множестваА.
Подмножество
![]() называется собственным подмножеством
множестваВ(
называется собственным подмножеством
множестваВ(![]() - строгое включение), еслиАне пусто и не совпадает сВ.
Например, имеют место строгие включения:N
- строгое включение), еслиАне пусто и не совпадает сВ.
Например, имеют место строгие включения:N![]() Z
Z![]() Q
Q![]() R.
R.
Определим понятие равенства множеств:А=В тогда
и только тогда, когда одновременно
выполняются два включения![]() и
и![]() ,
т.е. каждый элемент множестваАявляется элементом множестваВи каждый элемент множестваВявляется элементом множестваА:
,
т.е. каждый элемент множестваАявляется элементом множестваВи каждый элемент множестваВявляется элементом множестваА:
![]()
Свойства равенства множеств:
1) для любого АсправедливоА=A;
2) если А=В, то иВ=A;
3) если А=ВиВ=C, тоA=C.
1.1.4. Диаграммы Эйлера – Венна
Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.
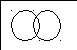
U
A B
Рис. 1.1 Диаграмма Эйлера-Венна
Универсальное множество Uизображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.1).
При этом возможны следующие случаи взаимного расположения двух множеств А иВ:
1) одно
из множеств строго включается в другое
(![]() или
или![]() );
);
2) множества равны;
3) множества не имеют общих элементов;
4) множества находятся в общем положении, т.е. не подходит ни один из вышеперечисленных случаев, и множества расположены как на рис. 1.1.
