
- •Экономическое моделирование
- •080504 – Государственное и муниципальное
- •Содержание
- •1. Общие сведения ………………………………………………………...4
- •2. Программа и методические указания …………………………………6
- •1. Общие сведения
- •2. Программа и методические указания
- •Введение
- •Межотраслевой баланс производства и распределения продукции
- •2.2.1 Содержание темы
- •2.2.2 Методические указания
- •Модели функционирования производства
- •2.3.1 Содержание темы
- •2.3.2 Методические указания
- •Макроэкономический прогноз
- •2.4.1 Содержание темы
- •2.4.2 Методические указания
- •Кооперативное принятие решений
- •2.5.1 Содержание темы
- •2.5.2 Методические указания
- •3. Темы практических и лабораторных работ
- •3.1 Темы практических работ.
- •3.2 Темы лабораторных работ.
- •4. Задания на контрольные работы
- •4.1 Методические указания
- •4.2 Контрольная работа № 1 «Межотраслевой баланс и макроэкономический прогноз»
- •Задания для контрольной работы № 1 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •4.3 Контрольная работа № 2 «Модели функционирования производства».
- •Задания для контрольной работы № 2
- •Содержание контрольной работы
- •5. Рекомендуемая литература
- •Федеральное агентство по образованию рф
- •Пример выполнения третьего задания контрольной работы №2
- •Пример выполнения контрольной работы №3
4.3 Контрольная работа № 2 «Модели функционирования производства».
Содержание контрольной работы
Определить номер варианта и привести полный текст задания.
В первой задаче рассматривается принцип открытого управления. Необходимо определить оценки эффективности, сообщаемые предприятиями, цену продукции и планы предприятий, назначаемые центром.
Во второй задаче действует принцип открытого управления со штрафами. Определить оценки эффективности, сообщаемые предприятиями центру.
В третьей задаче рассматривается принцип жесткого управления. Необходимо определить оценки, сообщаемые предприятиями центру, планы предприятий, назначаемых центром, и прибыль предприятий.
В четвертой задаче предприятия действуют в рыночных условиях. Определить цену продукции, объемы выпуска продукции и прибыль предприятий в равновесной ситуации.
В пятой задаче рассматривается полная децентрализация планирования. Необходимо определить, придут ли планы и цена к оптимальным при заданном законе ценообразования
 ,
если работает гипотеза слабого влияния.
,
если работает гипотеза слабого влияния.
Пример выполнения контрольной работы дан в приложении 2.
Задания для контрольной работы № 2
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
Вариант 7.
Вариант 8.
Вариант 9.
Вариант 10.
4.4. Контрольная работа №3 «Кооперативное принятие решений».
Содержание контрольной работы
Определить номер варианта и привести полный текст задания.
В первой задаче рассматриваются функции полезностей агентов (теория благосостояния). Необходимо определить полезности агентов для заданных ПКБ или ФКП, а также проверить заданное свойство указанного ПКБ.
Во второй задаче дана игра в форме характеристической функции. Предложено три произвольных дележа игры. Необходимо проверить, доминируют ли указанные дележи друг друга. Примечание: проверку производить по всем возможным коалициям.
В третьей задаче дана игра с распределением затрат с независимым спросом. Рассматривается коллективный объект, обслуживающий трех потребителей. Известны доходы агентов от использования объекта
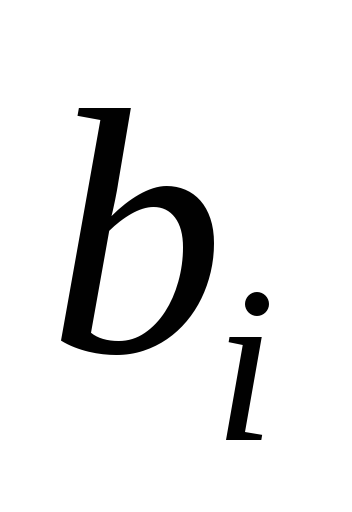 .
Затраты на обслуживание зависят от
того, какие агенты эксплуатируют объект
и определены в задаче для всех коалиций:
.
Затраты на обслуживание зависят от
того, какие агенты эксплуатируют объект
и определены в задаче для всех коалиций: .
Построить характеристическую функцию
игры, найти
.
Построить характеристическую функцию
игры, найти -ядро
(если оно существует).
-ядро
(если оно существует).В четвертой задаче рассматривается экономика общественного продукта с квазилинейными предпочтениями с двумя агентами (полезность агента
 равна
равна ,
где
,
где – плата за пользование общественным
продуктом). Известна функция затрат на
производство общественного продукта
– плата за пользование общественным
продуктом). Известна функция затрат на
производство общественного продукта .
Необходимо построить характеристическую
функцию игры, найти вектор Шепли,N-ядро
игры. Примечание:N-ядро
всегда является центром
.
Необходимо построить характеристическую
функцию игры, найти вектор Шепли,N-ядро
игры. Примечание:N-ядро
всегда является центром
 -ядра.
-ядра.
Пример выполнения контрольной работы дан в приложении 2.
Вариант 1
Определить эгалитарное и утилитарное решение, если функции полезности агентов равны, соответственно,
 ,
,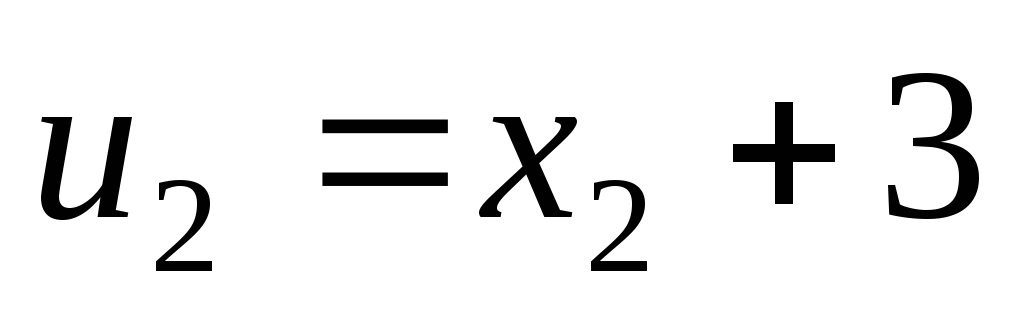 ,
и должно выполняться условие
,
и должно выполняться условие .
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция
.
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция .
.Характеристическая функция игры:




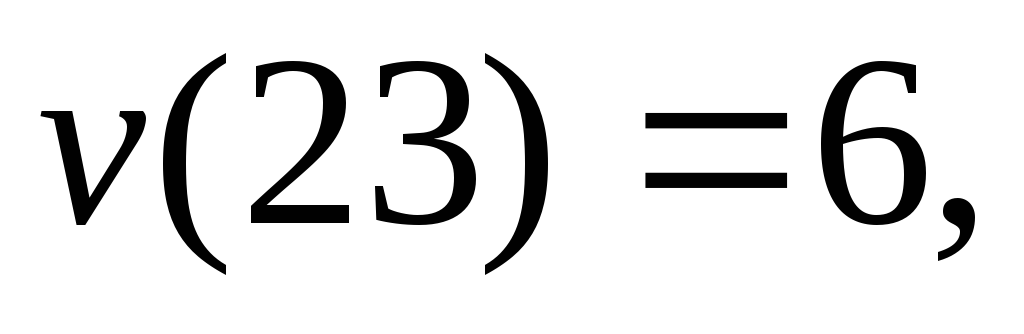
 .
Дележи:
.
Дележи: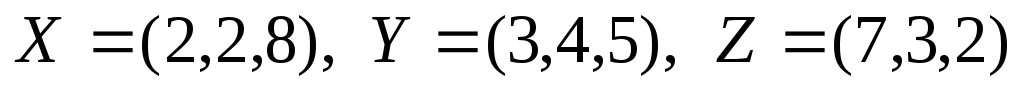 .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:
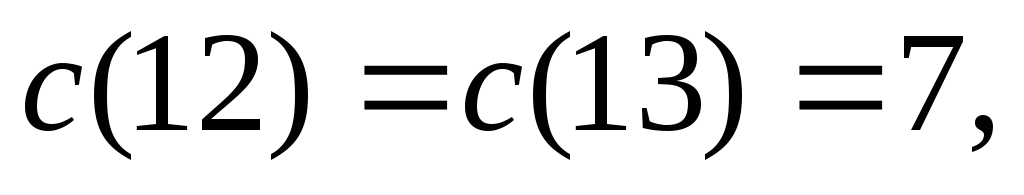

 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 2
Определить утилитарное решение и решения, оптимального по Нэшу, если функции полезности агентов равны

 при
при .
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
второго агента была уменьшена в два
раза.
.
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
второго агента была уменьшена в два
раза.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


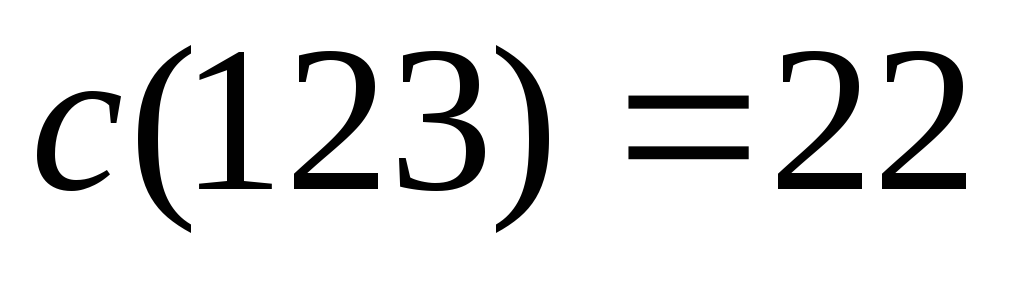 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов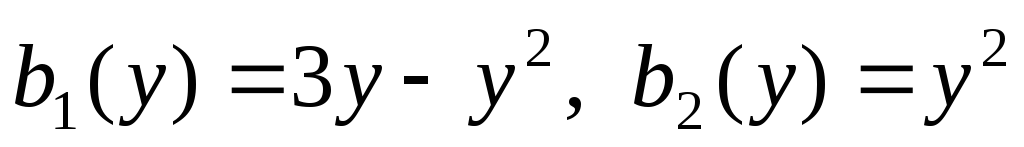 .
.
Вариант 3
Определить эгалитарное и диктаторское (диктат богатых) решение, если функции полезности агентов равны
 ,
, при
при .
Проверить независимость от общей шкалы
полезности для указанных ФКП, если к
функциям полезности агентов была
применена функция
.
Проверить независимость от общей шкалы
полезности для указанных ФКП, если к
функциям полезности агентов была
применена функция .
.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 4
Определить эгалитарное решение и решение, оптимальное по Нэшу, если функции полезности агентов равны

 при
при .
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
первого агента была увеличена в три
раза.
.
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
первого агента была увеличена в три
раза.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов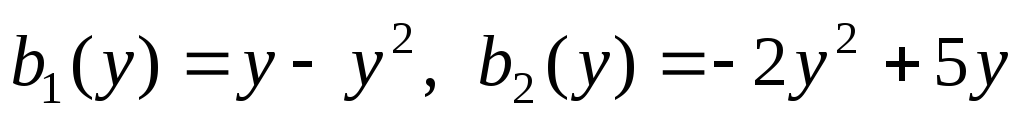 .
.
Вариант 5
Определить эгалитарное и утилитарное решение, если функции полезности агентов равны, соответственно,
 ,
, ,
и должно выполняться условие
,
и должно выполняться условие .
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция
.
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция .
.Характеристическая функция игры:




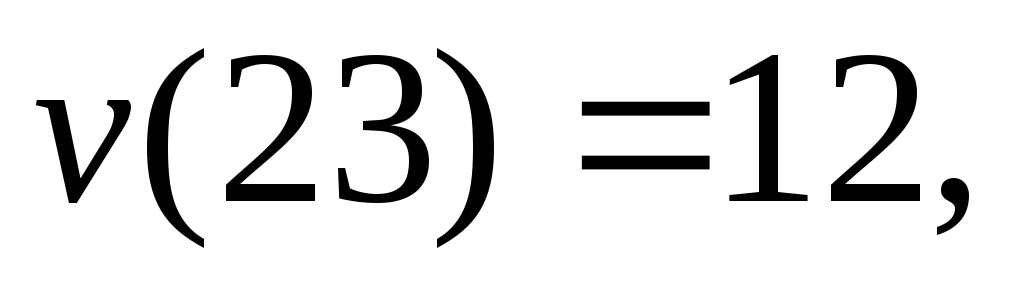
 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 6
Определить утилитарное решение и решения, оптимального по Нэшу, если функции полезности агентов равны

 при
при .
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
второго агента была увеличена в два
раза.
.
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
второго агента была увеличена в два
раза.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание: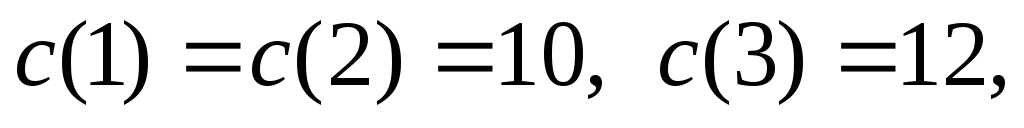


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов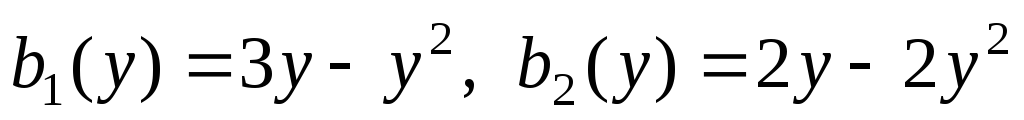 .
.
Вариант 7
Определить эгалитарное и утилитарное решения, если функции полезности агентов равны, соответственно,
 ,
, ,
и должно выполняться условие
,
и должно выполняться условие .
Проверить независимость от нуля для
указанных ПКБ, если первому агенту
выплатили дополнительно 5 единиц
полезности, а второму – только три
единицы.
.
Проверить независимость от нуля для
указанных ПКБ, если первому агенту
выплатили дополнительно 5 единиц
полезности, а второму – только три
единицы.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:
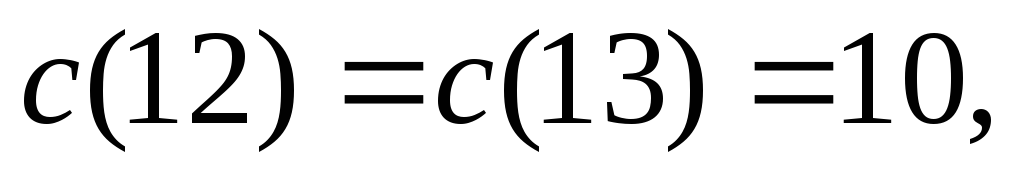

 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 8
Определить утилитарное решение и решения, оптимального по Нэшу, если функции полезности агентов равны

 при
при .
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
первого агента была уменьшена в три
раза.
.
Проверить независимость от масштаба
для указанных ПКБ, если функция полезности
первого агента была уменьшена в три
раза.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 9
Определить эгалитарное и утилитарное решение, если функции полезности агентов равны, соответственно,
 ,
, ,
и должно выполняться условие
,
и должно выполняться условие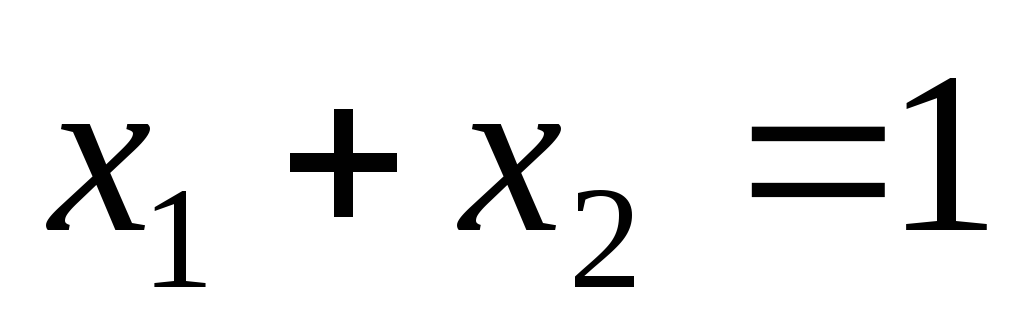 .
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция
.
Проверить независимость от общей шкалы
полезности для указанных решений, если
к функциям полезности агентов была
применена функция .
.Характеристическая функция игры:





 .
Дележи:
.
Дележи: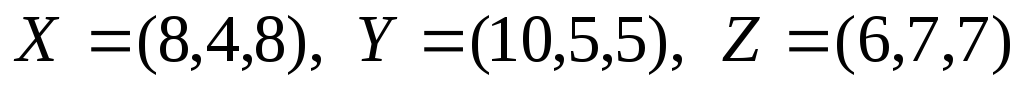 .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
Вариант 10
Определить эгалитарное и утилитарное решения, если функции полезности агентов равны, соответственно,
 ,
, ,
и должно выполняться условие
,
и должно выполняться условие .
Проверить независимость от нуля для
указанных ПКБ, если первому агенту
выплатили дополнительно 4 единицы
полезности, а второму – только две
единицы.
.
Проверить независимость от нуля для
указанных ПКБ, если первому агенту
выплатили дополнительно 4 единицы
полезности, а второму – только две
единицы.Характеристическая функция игры:





 .
Дележи:
.
Дележи: .
.Доходы агентов:
 .
Затраты коалиций на обслуживание:
.
Затраты коалиций на обслуживание:


 .
.Функция затрат
 ,
квазилинейные предпочтения агентов
,
квазилинейные предпочтения агентов .
.
