Теория прямоугольного волновода

5.1 Общие сведения.

Прямоугольный волновод (ПВ) - линия передачи СВЧ диапазона в виде металлической трубы прямоугольного сечения, заполненной однородным изотропным диэлектриком (чаще всего - воздух), рисунок 5.1. ПВ используется в сантиметровом и верхней части миллиметрового диапазонов. Для поперечных размеров ПВ приняты следующие обозначения: a - величина широкой стенки; b - величина узкой стенки, рисунок 5.1.

Величины a и b принято измерять в миллиметрах. Размеры ПВ, используемых в технике СВЧ, стандартизированы. Наиболее распространенными являются сечения 23х10 мм и 8х16 мм. Основными преимуществами ПВ, которые обусловливают их широкое применение в технике СВЧ, являются:

• полная помехозащищенность, т.к. ПВ является закрытой структурой, то внешние поля не проникают внутрь и поле распространяющейся в ПВ волны никак не влияет на окружающие объекты;

• малое затухание волны в ПВ;

• высокое значение пробивной мощности, что делает ПВ незаменимыми в качестве фидеров передающих антенн мощных передатчиков и радиолокационных станций.

К недостаткам ПВ следует отнести большую массу и габариты, что ограничивает возможности их использования в составе бортовой аппаратуры искусственных спутников Земли и других космических аппаратов. Однако, современные технологии позволяют изготавливать ПВ путем напыления слоя серебра на внутреннюю поверхность прямоугольной трубы, изготовленной из пластика, что существенно уменьшает массу ПВ.

 

5.2 Расчет полей в пв.

Собственными волнами называют свободные гармонические электромагнитные волны в прямоугольном волноводе с идеально проводящими стенками, заполненном диэлектриком без потерь.

5.2.1 Постановка задачи. Для определения полей собственных волн в ПВ необходимо решить однородные уравнения Гельмгольца относительно комплексных амплитуд напряженностей электрического и магнитногополей:

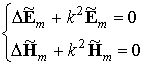(5.1)

при граничных условиях на идеально проводящих стенках волновода:

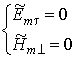,(5.2)

где: k - волновое число в свободном пространстве - ;

и - тангенциальная и нормальная составляющие комплексных амплитуд напряженностей электрического и магнитного полей.

В силу продольной однородности геометрических и физических параметров ПВ решение задачи (5.1)-(5.2) можно представить в виде волн, бегущих вдоль оси Oz:

,(5.3)

где  - постоянная распространения волны.

Функции иописывают распределение полей в поперечном сечении ПВ. Подставив (5.3) в (5.1), получим двумерные уравнения для нахождения этих функций:

,(5.4)

где: - двумерный оператор Лапласа;

- поперечное волновое число.

Векторные уравнения (5.4) распадаются на скалярные уравнения для x , y и z компонент полей и, т.е. нахождение полей собственных волн ПВ сводится к решению 6 скалярных уравнений Гельмгольца в поперечном сечении ПВ. Для удовлетворения граничным условиям на идеально проводящих стенках необходимо знать распределения на них поверхностных зарядов и токов, однако они не известны заранее. Поэтому решение скалярных уравнений можно получить только для продольных компонент полейE_mz и H_mz, т.к. они удовлетворяют простым и одинаковым на всех стенках условиям:

,

где - производная по нормали к стенке волновода.

5.2.2 Классы собственных волн ПВ. Легко убедится, что поставленные задачи для продольных компонент имеют нулевые решения: E_mz=0 и H_mz=0. На основании этого выделяют два класса собственных волн ПВ: E-волны - это собственные волны ПВ, у которых имеется продольная составляющая только электрического поля E_z, а H_z=0; H-волны - это собственные волны ПВ, у которых имеется продольная составляющая H_z, а E_z=0. E-волны называют также электрическими или поперечно-магнитными волнами (ТМ-волнами). Н-волны называют, соответственно, магнитными или поперечно-электрическими. Второе название отражает тот факт, что для Е-(Н-) волн вектор магнитного (электрического) поля лежит в плоскости поперечного сечения ПВ (плоскость z=const на рисунке 5.1). Собственную волну ПВ, у которой иможно представить в виде суперпозиции E - и H-волн. Такие волны называют гибридными.

Поперечные компоненты полей:

выражаются через E_mz и H_mz при помощи уравнений Максвелла:

,(5.5)

где - двумерный оператор Гамильтона;

x₀, y₀, z₀ - орты прямоугольной системы координат.

Подставив в (5.5) решение скалярного уравнения Гельмгольца для при условиимы получим выражения для поперечных компонент E-волны. Аналогично получаются выражения для поперечных компонент полей H-волны.

Итак, расчет полей собственных волн ПВ сводится к решению двух задач:

E-волны: (5.6)

H-волны: 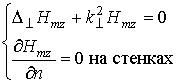(5.7)

5.2.3 Типы собственных волн ПВ. Используя метод разделения переменных, легко получить решения задач (5.6) и (5.7), удовлетворяющие граничным условиям при x=(0; a) и y=(0; b) (рисунок 5.1):

, (5.8)

где иопределяют амплитуды полей;

n и m - целые числа.

Остальные компоненты полей определяются дифференцированием E_mz или H_mz в соответствии с (5.5). Каждому набору двух целых чисел (n,m) соответствует свое распределение поля в ПВ, т.е. набор (n,m) определяет тип собственной волны в ПВ. Другими словами, существует множество типов E- и H-волн. Для них приняты следующие обозначения: E_nm и H_nm.