Норма матрицы

Проблема собственных значений определена только для квадратных матриц. В экономической практике часто необходимо оценивать не только квадратные матрицы. Для такой оценки можно использовать универсальное понятие нормы, справедливое для матриц любой размерности.

Нормой произвольной матрицы А называется действительное число , удовлетворяющее целому ряду условий, наиболее важными из которых являются:

1. , причемтолько в случае полностью нулевой матрицыА.

2. , где.

В какой–то степени нормуможно образно представлять как показатель “толщины” или “мощности” матрицыА.

Норма называется канонической, если , т.е. она не меньше, по модулю, любого элемента матрицыА. При выборе нормы возможно использовать самые разнообразные соображения, не противоречащие определению. Однако на практике обычно достаточно следующих канонических норм:

1. m–норма – суммируются, по модулю, всестроки матрицы А и максимальная из полученных сумм объявляется нормой.

2. l–норма – суммируются, по модулю, всестолбцы матрицы А и максимальная из полученных сумм объявляется нормой.

3. k–норма =– суммируются квадраты всех элементов матрицыА и корень из этой суммы объявляется нормой.

Векторы Основные определения и понятия

Частный случай матрицы, состоящей из одного столбца, имеет широкое самостоятельное применение. Геометрическое изображение вектора направленным отрезком, известное из школьного курса, можно определить как совокупность проекций вектор-отрезка, записанных в виде матрицы-столбца. Тогда имеем понятие свободного вектора, не зависящего от точки приложения, которая может быть как в начале координат (радиус-вектор), так и в любой точке пространства. Направление вектора всегда строго сохраняется. Для двумерного случая:= или = ; = или = . Для общности, все проекции в дальнейшем обозначаются через хи называютсякоординатами вектора. Если какая-то проекция хотрицательна, то она откладывается в противоположную сторону соответствующей оси координат.

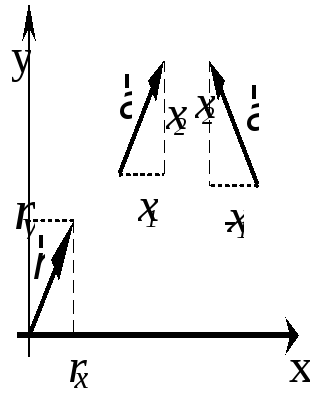
Совершенно так же выглядят векторы = в трехмерной системе координат - добавляется координата z. Но векторы размерности более трех наглядно не представимы - они могут быть поняты только по аналогии. Общее определение: вектором в n-мерном пространстве называется упорядоченный набор n координат = , число которых равно размерности пространства, т.е. n.

Длина вектора определяется формулой d=. Все операции с векторами - те же, что и матрицами.

Рассмотрим линейную комбинацию трех векторов: k+k+k.

Если равенство k+k+k=0 возможно только при k=k=k=0, то векторы,иназываютсялинейно независимыми. Иначе, по крайней мере, один из векторов можно выразить суммой двух других и векторы будут линейно зависимыми . Например, при k0 можно записать:=(- k- k).

Максимально возможное число линейно независимых векторов равно размерности пространства. Так, для плоскости возможны только два таких вектора, для прямой - один. Для n-мерного пространства число векторов равно n.

Пусть на плоскости имеются векторы , и . Покажем, что они линейно зависимы. Составим их линейную комбинацию: k + k+ k = 0 и перейдем к алгебраической форме:

.

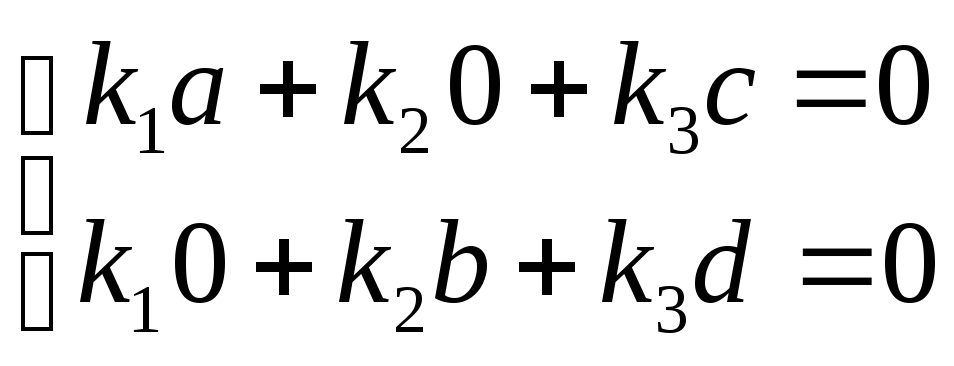
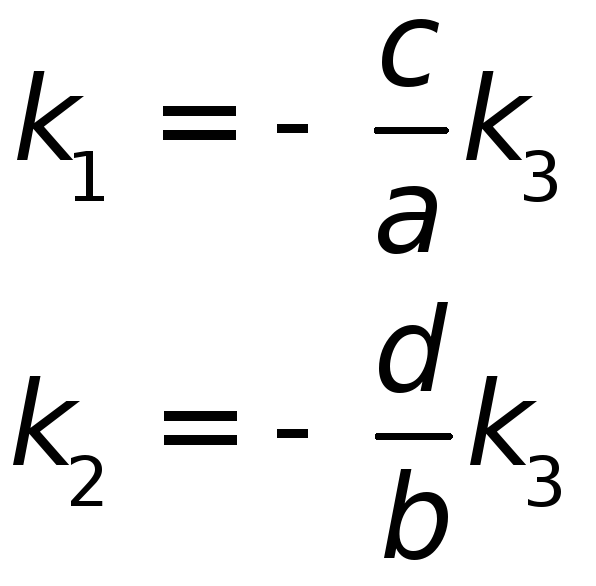Таким образом, положив k=1, имеем:-+=0 или =+, т.е. третий вектор не является независимым и выражается суммой двух других или разлагается по двум другим векторам. Рассмотрим первые два вектора подробнее: =а=аи=b=b. Тогда=с+d- очень компактная запись черезединичные векторы (или орты). Покажем, что орты линейно независимы: k+ k= k+k=0 или 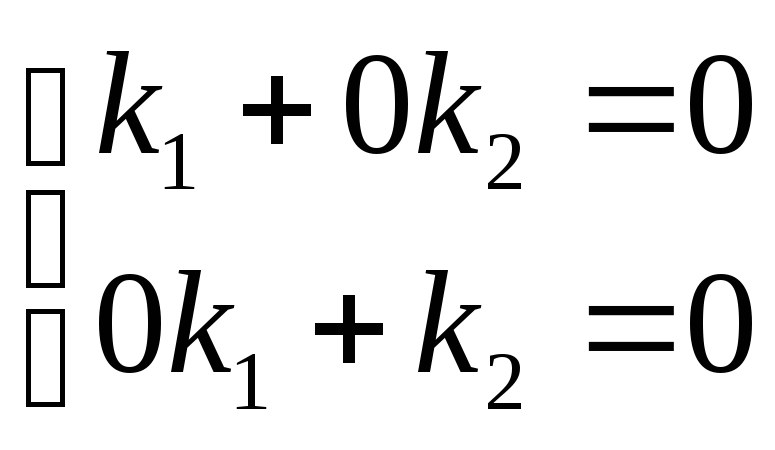, откуда k=k=0.

Так как с и d произвольны, то, очевидно, любой вектор на плоскости можно представить комбинацией двух ортов и. Это называется разложением вектора по единичномубазису или, точнее, по ортонормированному, т.к. длина каждого орта равна 1. Конечно, можно разлагать не по ортам, а по двум любым линейно независимым векторам (по общему базису), к примеру, и, но разложение с помощью ортов является и простым, и общим.

Все введенные выше понятия справедливы для пространства любой размерности. В n-мерном пространстве всегда имеются n линейно независимых ортов =,=,...,=, поэтому любой векторможно разложить по ортонормированному базису:=а₁₊а₂+...+а_n. Разложение векторов по базису из линейно независимых векторов всегда единственно в любом принятом базисе.