Матрицы Определения

Матрицей А называется прямоугольная таблица чисел, имеющая m строк и n столбцов, т.е. размерность mn (m, nN). Примеры:

А= = - прямоугольная;

А= - квадратная;

А=-строка (или: матрица-строка); =А= - вектор (или: матрица-столбец); Е= - единичная (всегда квадратная); А_д= - диагональная (тоже всегда квадратная).

Квадратная матрица называется симметричной, если a=a при ij.

Заметим, что матрица качественно отличается от определителя. Матрица - не число, а нераздельное множество чисел, представленное в виде таблицы. Только квадратные матрицы можно связать с определителями, которые в этом случае будут иметь статус некоторой полезной характеристики при операциях с квадратными матрицами.

Матрицы имеют большое практическое значение, т.к. многие объекты и процессы проще всего описывать именно матрицами.

Операции над матрицами

1. Две матрицы А и В равны, если они имеют одинаковую размерность и a=b, т.е. равны соответственно расположенные элементы.

2. Две матрицы одинаковой размерности можно суммировать: С=А+В, причем результатом будет поэлементная сумма: с=а+в:

=+=.

3. Матрицу любой размерности можно умножить на число . Это значит - умножить на это число все элементы матрицы:А=(а)=(а)

4. Матрицу А можно умножить на матрицу Втогда и только тогда, когда число столбцов у А, т.е. n, равно числу строк у В. Результатом будет матрица С. Элемент сэтой матрицы равен сумме произведений элементов строки №i в матрице А на элементы столбца № j в матрице В. Примеры:

=;

=;=.

Несколько матриц множим по очереди: АВС=(АВ)С=D.

Отметим, что, в отличие от числовой арифметики, матрицы редко подчиняются правилу АВ=ВА. Чаще всего АВВА, если такая перестановка в принципе возможна. В немногих случаях, когда равенство соблюдается, А и В называются коммутирующими матрицами. Особого практического значения они не имеют.

Транспонирование матриц и его свойства

Так же, как в определителях, транспонирование - это замена строк столбцами: если А= , то А=. Приведем основные свойства транспонирования, которые легко доказываются вычислением:

1. Двойное транспонирование возвращает исходную матрицу: (А)=А.

2. Транспонирование суммы матриц эквивалентно сумме транспонированных слагаемых: (А+В)=А+В.

3. Транспонирование произведения двух матриц эквивалентно произведению транспонированных матриц, взятых в обратном порядке: (АВ)=ВА.

4. Произведение матрицы на свою транспонированную: АА или ААвсегда имеет результатом симметричную квадратную матрицу.

5. Если матрица А - квадратная, то значение ее определителя не зависит от транспонирования: D(A)=D(A).

Обратная матрица

Понятие обратной матрицы определено только для квадратных матриц, определитель которых не равен нулю. Если D=0, то заданная матрица обратной не имеет и называется особенной (или вырожденной).

Матрица Аназывается обратной по отношению к матрице А, если выполняется равенство: АА=АА=Е.

Алгоритм вычисления А покажем на примере А=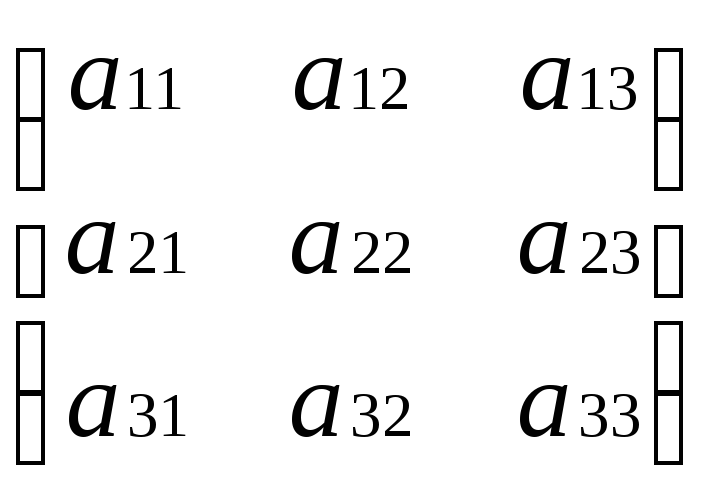 по шагам:

1. Вычисляем определитель D=. Если D=0, то работа прекращается с заключением:А - вырожденная матрица.

2. Вычисляем все адъюнкты матрицы А: А=Ad, A=Ad, ... A=Ad.

3. Из вычисленных адъюнктов составляем союзную (или присоединенную) матрицу А^с=. Обратим внимание, что индексы этой матрицы транспонированы по отношению к исходной матрице А.

4. Вычисляем обратную матрицу А=А^с

5. Если расчет проводится вручную, то выполняется проверка: АА= Е или AA=Е.

Перечислим основные свойства обратной матрицы:

1. D(A)=.

2. (АВ)=ВА, т.е. при раскрытии скобок порядок сомножителей меняется на обратный.

3. (А)=(А), т.е. операции обращения и транспонирования можно менять местами.

В заключение отметим, что из-за арифметического объема работы с определителями, использование описанной процедуры ограничивается матрицами второго и третьего порядков.