Общее уравнение прямой линии

Общее уравнение прямой линии имеет вид Ах+Ву+С=0, где А, В, СR. Другая форма записи (нормализованное уравнение) у=кх+b, где к= -, b= -. Отметим, что к=tg, где- угол наклона прямой к оси Х. Придавая нулевые значения коэффициентам, получим варианты общего уравнения:

А=0: Ву+С= 0 или у=b - прямая, параллельная оси оХ;

В=0: Ах+С=0 или х= -- прямая, параллельная оси оY;

С=0: Ах+Ву=0 или у=кх - прямая проходит через начало координат;

А=В=С=0 - вырождение прямой.

Таким образом, всякое невырожденное уравнение первой степени Ах+Ву+С=0 при являетсяуравнением прямой линии на плоскости.

Если на плоскости имеются две прямые А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0, то их взаимодействие описывается четырьмя случаями:

1. Точка пересечения прямых определится из системы уравнений:

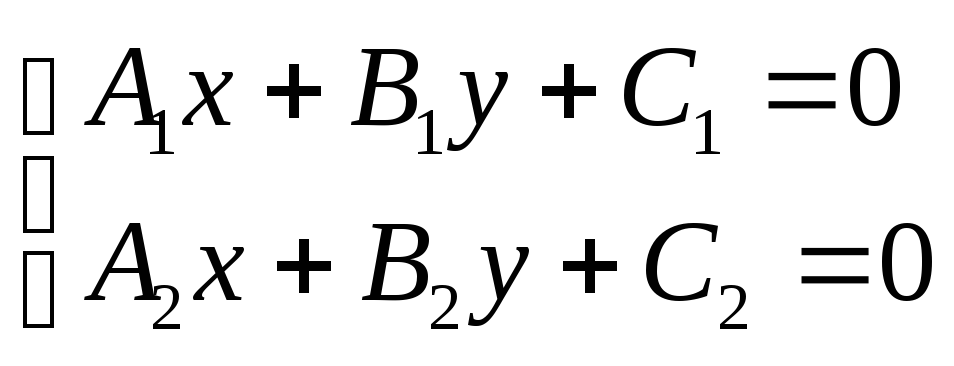или .

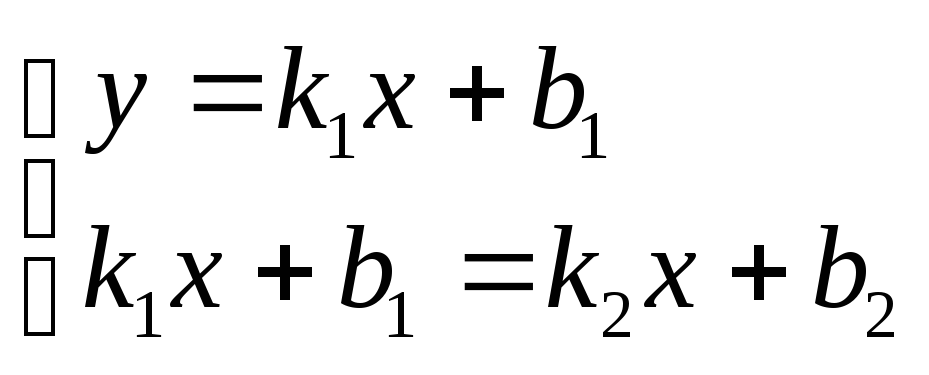2. Если прямые параллельны, то соблюдается условие:

к₁=к_2.

3. Если прямые перпендикулярны, то соблюдается условие:

А₁А₂+В₁В₂=0 или .

4. Угол между прямыми определится из условия:

tg =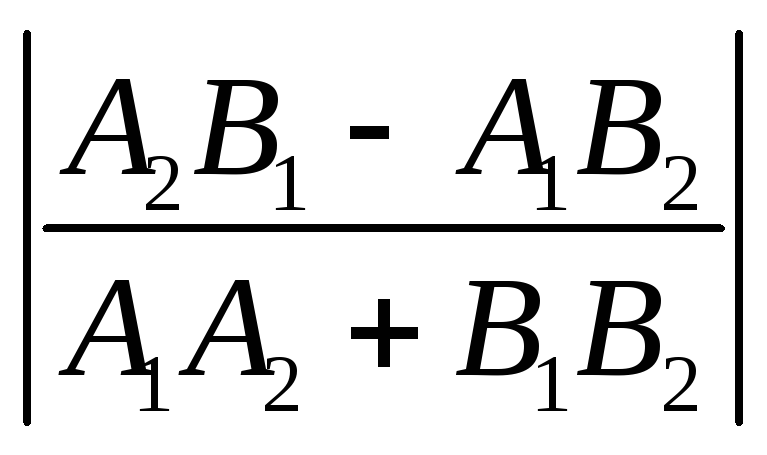или tg=.

Здесь знак модуля взят для обеспечения положительного результата.

Варианты уравнения прямой

На практике часто встречаются случаи, когда надо получить уравнение прямой не только с помощью приведенных выше общего и нормализованного уравнений. Рассмотрим некоторые такие случаи.

1. Известно, что прямая образует с оХ угол и проходит через известную точку М(а; b). Найти уравнение (прямая через точку по заданному направлению).

Так как известно, то к=tg. Тогда уравнение прямой

Это уравнение легко преобразуется в уже известные формы записи.

Из прямоугольного треугольника MNP определяем

Тогда

2. Известны точки М(а; b) и N(c; d). Найти уравнение проведенной через них прямой (прямая через две точки).

После преобразования получим

=.

Если а=с или b =d, то следует использовать другую форму записи:

(х-а)(d-b)=(y-b)(c-a).

Искомое уравнение имеет вид

.

Отметим, что, если прямая параллельна оси оХ или оY, то такое уравнение составить нельзя - нет отрезка.

3. Известны отрезки а и b, которые прямая отсекает от осей координат. Найти уравнение этой прямой (уравнение прямой в отрезках).

Построение прямых. Расстояния

Приведем некоторые типовые задачи, часто встречающиеся в практике.

1. Пусть известна прямая Ах+Ву+С=0 (или у=кх+b ) и требуется провести новую прямую, проходящую через точку М(c; d) параллельно данной.

Искомое уравнение имеет вид:

A(x-c)+B(y-d)=0

или

y-d=k(x-c),

где к уже известно.

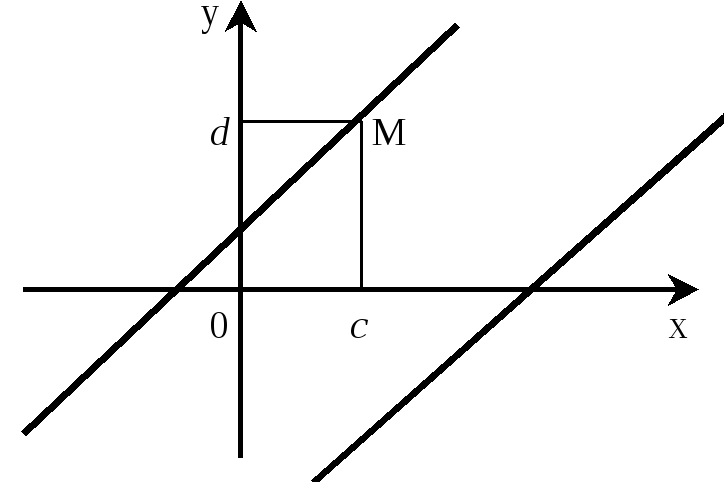
2. Пусть известна прямая Ах+Ву+С=0 (или у=кх+b) и требуется провести новую прямую, проходящую через точку М(c; d) перпендикулярно данной.

Искомое уравнение имеет вид

или

y-d = - (x-c).

3. Требуется определить расстояние между точками М(a; b) и N(c;d).

Задача решается с помощью теоремы Пифагора. Искомая формула имеет вид (длина отрезка):

l=.

4. Известны прямая Ах+Ву+С=0 (или у=кх+b) и точка N(c; d), не лежащая на этой прямой. Требуется определить расстояние от точки до данной прямой.

Искомая формула имеет вид

l=или

l=.

Модуль - для обеспечения положительного результата.