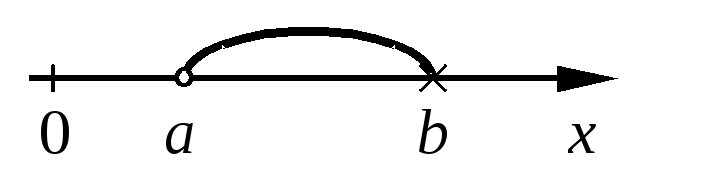- •Содержание
- •Введение
- •Основные понятия теории множеств Определения, термины и символы
- •Операции над множествами
- •Основные числовые множества
- •Функция Определение и свойства функции
- •Классификация функций
- •Вычисление значений функции
- •Общее уравнение прямой линии
- •Варианты уравнения прямой
- •Построение прямых. Расстояния
- •Определители Определители второго и третьего порядков
- •Основные свойства определителей
- •Определители и системы линейных уравнений
- •Матрицы Определения
- •Операции над матрицами
- •Транспонирование матриц и его свойства
- •Обратная матрица
- •Матричные уравнения
- •Степень и функции матриц
- •Понятие о проблеме собственных значений матрицы
- •Норма матрицы
- •Векторы Основные определения и понятия
- •Скалярное произведение векторов
- •Пределы Общее понятие предела переменной величины
- •Предел функции
- •Бесконечно малые (б.М.) и бесконечно большие (б.Б.) величины
- •Теоремы о пределах
- •Замечательные пределы
- •Вычисление пределов
- •Непрерывность и разрывы функции
- •Производная и дифференциал функции Определения. Геометрический и физический смысл
- •Табличные производные
- •Теоремы дифференцирования
- •Применения производной Вычисление пределов по правилу Лопиталя
- •Возрастание и убывание функции
- •Экстремумы функции
- •Изгибы функции и их определение
- •Асимптоты функции
- •Общая схема исследования функции и построения графиков
- •Неопределенный интеграл Первообразная функция и неопределенный интеграл
- •Свойства неопределенного интеграла
- •Интегралы от основных элементарных функций
- •Непосредственное интегрирование (метод разложения)
- •Метод замены переменной
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Систематическое интегрирование
- •Понятие о дифференциальных уравнениях
- •Уравнения первого порядка с разделяющимися переменными
- •Понятие о дифференциальных уравнениях второго порядка
- •Определенный интеграл Определения
- •Свойства определенного интеграла
- •Основные методы интегрирования
- •Интеграл с переменным верхним пределом
- •Несобственные интегралы
- •Применение определенного интеграла к вычислению площадей
- •Теорема о среднем определенного интеграла
- •Формула трапеций
- •Функции нескольких переменных Основные понятия
- •Частные производные и дифференциалы
- •Градиент функции двух переменных
- •Производные высших порядков
- •Абсолютные экстремумы функции двух переменных
- •Интегрирование функции двух переменных
- •Литература
Основные числовые множества
В процессе получения количественных результатов мы постоянно имеем дело с множествами чисел. Приведем классификацию числовых множеств:
1. Натуральные числа N={n}={1; 2; 3;…; n;…}.
2.
Неотрицательные
числа
![]() .
.
3.
Целые числа
![]()
![]() .
.
4.
Рациональные
числа
![]() ,
где
,
где![]() .
.
5.
Действительные
числа
![]() ,
полная совокупность рациональных и
иррациональных чисел.
,
полная совокупность рациональных и
иррациональных чисел.
Очевидно:
![]() ,
т.е. каждое числовое множество является
подмножеством следующего.
,
т.е. каждое числовое множество является
подмножеством следующего.
Все
эти числовые множества обладают свойством
упорядоченности,
т.е. для любых двух элементов a
и b
любого
множества можно указать, что либо![]() ,
либо
,
либо![]() .
Для трех различных элементовa,
b
и c выполняется
свойство транзитивности:
из
.
Для трех различных элементовa,
b
и c выполняется
свойство транзитивности:
из
![]() и
и![]() следует, что
следует, что![]() .
.
Ясно,
что все числовые множества – бесконечны,
причем N,
![]() ,Z и
Q – счетные
(т.е. элементы этих множеств можно
перенумеровать), R
– несчетное
множество.
,Z и
Q – счетные
(т.е. элементы этих множеств можно
перенумеровать), R
– несчетное
множество.
При практических расчетах мы достаточно часто имеем дело не со всем числовым множеством, а с его некоторой частью, т.е. подмножеством. Изображение подмножеств числовых множеств удобно иллюстрировать с помощью числовой оси, которая в этом случае является вариантом диаграммы Эйлера-Венна. Напомним, что числовой осью называется линия (чаще всего – прямая), на которой указаны: начало отсчета, направление отсчета и единица измерения. Для удобства примем, что если конец интервала является элементом описываемого множества, то он обозначается кружочком, а если нет, то – крестиком. Тогда основные типы интервалов определяются следующим образом:
|
|
(a,
b)
или
|
|
|
|
|
|
|
|
|
|
Для
оценивания множеств на практике удобно
использовать дополнительные характеристики.
Пусть A –
произвольное,
но не пустое множество. Число
![]() называетсямаксимумом
множества
A,
если
называетсямаксимумом
множества
A,
если
![]() и любые другие элементы множества не
превосходят этого числа:
и любые другие элементы множества не
превосходят этого числа:![]() .
Аналогично определяется иминимум
множества
.
Аналогично определяется иминимум
множества
![]() .
.
Множество
A
называется ограниченным
сверху,
если существует число k,
такое, что для всех элементов множества
справедливо
![]() .
Это число назовемверхней
гранью
(или мажорантой) множества A.
Минимально возможное значение k
называется точной
верхней гранью
множества A
и обозначается
.
Это число назовемверхней
гранью
(или мажорантой) множества A.
Минимально возможное значение k
называется точной
верхней гранью
множества A
и обозначается
![]() (supremum A).
(supremum A).
Множество
A называется
ограниченным
снизу,
если существует число p,
такое, что что для всех элементов
множества справедливо
![]() .
Это число назовемнижней
гранью
(или минорантой) множества A.
Максимально возможное значение p
называется точной
нижней гранью
множества A
и обозначается
.
Это число назовемнижней
гранью
(или минорантой) множества A.
Максимально возможное значение p
называется точной
нижней гранью
множества A
и обозначается
![]() (infimum A).
(infimum A).