Основные методы интегрирования

Для того, чтобы вычислить определенный интеграл, достаточно найти первообразную и затем применить формулу Ньютона-Лейбница. Некоторое ускорение (чисто арифметическое) процесса интегрирования можно получить с помощью более ранней подстановки пределов интегрирования.

1. Интегрирование по частям. Можно использовать формулу в следующем виде:

.

Отметим, что по сравнению с формулой выигрыш в скорости расчета невелик.

2. Замена переменной. В этом случае раннее преобразование пределов интегрирования по принятой формуле подстановки может привести к хорошему ускорению, т.к. отпадает необходимость обратной замены. Общая формула имеет вид

, где .

Для ясности, приведем пример:

.

Интеграл с переменным верхним пределом

В практических задачах часто встречаются случаи, когда имеется начальная точка интервала интегрирования, т.е., а конец интервала еще не известен. Определенный интеграл вполне можно применить и для таких задач, если известен закон образования верхнего предела; в простейшем варианте. Формула Ньютона-Лейбница применяется обычным образом, однако результатом будет не число, афункция:

.

Изменение обозначения переменной интегрирования - чисто психологическое, во избежание путаницы при вычислениях.

Несобственные интегралы

Если предел интегрирования может быть переменным, то легко представить случай, когда он переходит в бесконечность. Интегралы с одним или обоими бесконечными пределами получили название несобственных интегралов первого рода. Здесь также можно, на практике, использовать формулу Ньютона-Лейбница, однако следует помнить, что символ -не число, а условное обозначение неограниченного возрастания (или убывания) аргумента в процессе изменения. Т.е., со строгих позиций, вычисление несобственного интеграла первого рода – это вычисление некоторого предела, с постоянным использованием теорем о бесконечно малых и бесконечно больших величинах, приведенных ранее в теме 6 Пределы. Таким образом:

;

;

.

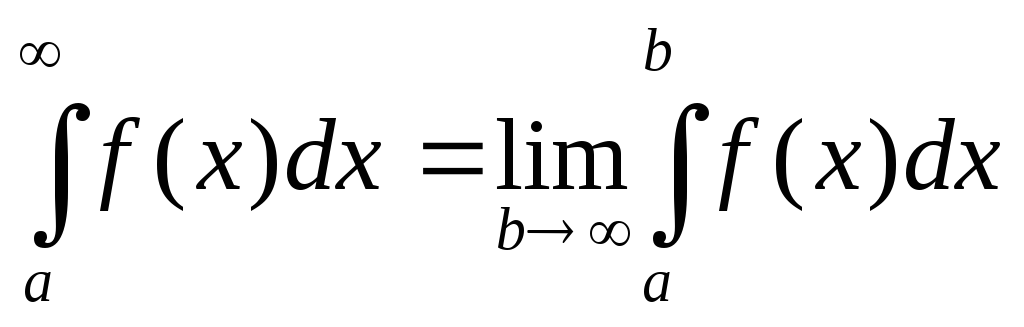Т.е., символы бесконечности условно заменяются буквенными параметрами, применяется формула Ньютона-Лейбница, после чего обычным образом вычисляются пределы. Если в результате такого расчета получится число А (включая 0), то ответ следует записать в форме: интеграл сходится к значению А. Если же результатом будет (или), то ответ:интеграл расходится.

При практических вычислениях, как демонстрируется далее в разделе 10.9, вполне допустимо не использовать в явной форме операторы , ноне следует забывать о том, что на самом деле вычисляются пределы, а не конкретные числовые значения.

Следующим видом несобственных интегралов являются интегралы от функций с разрывом на одном (или обоих) конце интервала интегрирования или с разрывом внутри интервала интегрирования. Например: и т.п. Такие интегралы носят названиенесобственных интегралов второго рода. Эти интегралы очень опасны, т.к. часто выглядят вполне безобидно, но применение формулы Ньютона-Лейбница приводит к неверным результатам.

Вычисление интегралов второго рода осуществляется приведением к интегралам первого рода (или сумме таких интегралов), т.е. ставится задача вычисления предела относительно точки, в которой подынтегральная функция разрывна. Здесь не будем подробно останавливаться на схеме вычисления таких интегралов, т.к., если в прикладной задаче появился интеграл второго рода, то это свидетельствует либо об ошибке расчетчика, либо о некорректности всей математической модели для данной задачи и необходимости изменения этой модели.