Изгибы функции и их определение

В целом ряде практически важных случаев анализа деталей процессов необходимо более подробно описывать изменяемость функции у=f(x) на интервале:

Назовем функцию выпуклой вверх (или просто -выпуклой) на интервале , если значения функции на этом интервале находятсявыше отрезка, соединяющего точки иивогнутой (или выпуклой вниз), если ее значения находятся ниже такого отрезка. Точку с, в которой выпуклость сменяется вогнутостью (или наоборот) назовем точкой перегиба функции .

Выпуклость, вогнутость и точки перегиба определяются и анализируются с помощью второй производной по следующим правилам:

1. Если значения второй производной на интервалеотрицательны, то функция выпукла на этом интервале.

2. Если значения второй производной на интервалеположительны, то функция вогнута на этом интервале.

3. Необходимым условием для точки перегиба является то, что в ней вторая производная либо равна нулю, либо бесконечна, либо не существует. Еслипри переходе через эту точку меняет знак, то это -достаточное условие перегиба.

Таким образом, для исследования функции на изгибы и точки перегиба, можно использовать следующую схему:

1. Определяем производную .

2. Находим стационарные точки из анализа области определения второй производной и решения уравнения .

3. Определяем знаки второй производной в интервалах между вычисленными точками и устанавливаем наличие точек перегиба и типы изгиба функции.

Асимптоты функции

Следующей дополнительной характеристикой функции являютсяасимптоты. Это - прямые, к которым стремится график функции при неограниченном возрастании (или убывании) аргумента. Существуют три вида асимптот, которые поясним чертежом:

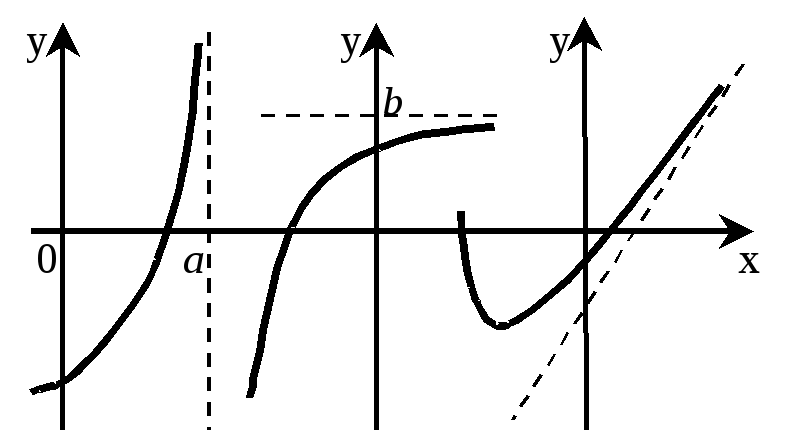
Приведем, без доказательств, технику определения асимптот:

1. Вертикальные асимптоты х=а находятся из анализа области определения функции . Например,у=не определена в точкех=2, следовательно, х=2 и есть вертикальная асимптота.

2. Если существует предел или (или оба вместе), то уравнения у= b или (и) у=с определяют горизонтальные асимптоты.

3. Если существуют конечные пределы и , причем оба одновременно, то прямая у=аx+b является наклонной асимптотой графика функции .

Общая схема исследования функции и построения графиков

В современных условиях построение графиков осуществляется на практике, как правило, по точкам или с помощью компьютера. Однако в задачах с повышенной ответственностью необходимо использовать описанные выше приемы. Полная последовательность анализа функции и построения ее графика состоит из следующих этапов:

1. Находится область определения функции и вертикальные асимптоты, если они есть.

2. Устанавливается тип функции: четная, нечетная, общего вида.

3. Из решения уравнения определяютсякорни функции, т.е. точки ее пересечения с осью оХ.

4. Вычисляются производные и.

5. Определяются экстремумы функции.

6. Определяются точки перегиба и исследуются выпуклости функции.

7. Проверяется наличие горизонтальных и наклонных асимптот.

8. При необходимости детализации, вычисляются значения функции в нескольких дополнительных точках.

9. Все полученные результаты отображаются на плоскости, и строится график.

Расчеты и отображение результатов обычно делаются одновременно. Этапы 2, 6 и 7, во многих случаях, можно опустить.