Производная и дифференциал функции Определения. Геометрический и физический смысл

Приращением функции у=f(x) в интервале х называется разность у=f(х+х)-f(x). Если у>0, то функция на интервале возрастает; при у<0 - убывает; при у=0 – не изменяется.

Предел отношения приращения функции у к приращению аргумента х при стремлении х к нулю называется производной функции:

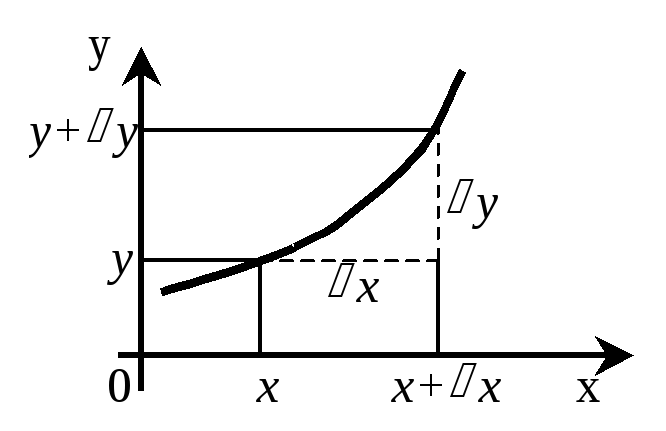
Другие, эквивалентные, обозначения:

.

Геометрический смысл производной тесно связан с понятием касательной.

Проведем через точку М секущую ММ₁. Если точку М₁ устремить к М, т.е. уменьшать х до нуля, то в момент слияния точек М и М₁ угол перейдет в угол: tg=;

Следовательно, производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

С физической точки зрения производная - скорость изменения функции в данной точке.

Если функция имеет единственную производную в точке, она называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала a,называется дифференцируемой в данном интервале.

Табличные производные

С помощью определения можно вычислять производные функций. Пример:

y= f(x)=x² f(x+x)=( x+x)²=x²+2xx+(x)² y= f(x+x) - f(x)=2xx+(x)².

Отсюда и .

Совершенно аналогично можно получить и производные любых других функций. На этой основе разработана и постоянно используется стандартная таблица производных:

1	у=С	С - постоянная (число)
2	у=xa	aR
3	у=sin x
4	у=cos x
5	у=tg x
6	у=ctg x
7	у=ax	axln a
8	у=ex	ex
9	у=logax	logae
10	у=ln x
11	у=arcsin x
12	у= arccos x	-
13	у=arctg x
14	у=arcctg x	-

Теоремы дифференцирования

Так же, как и при вычислении пределов, математика разработала ряд теорем, ускоряющих вычислительную работу. Приведем их без доказательств:

1. Сумма: у=u(x)v(x) .

2. Произведение: y=uv .

3. Частное: y= .

4. Постоянный множитель: y=Cu .

Производная сложной функции

Как было показано в теме 2 Функция, сложную функцию следует заменить эквивалентной системой. После этого полученную систему дифференцируем по каждому уравнению системы. Окончательный результат получается как произведение промежуточных:

1. у=f₁(f₂(x)) .

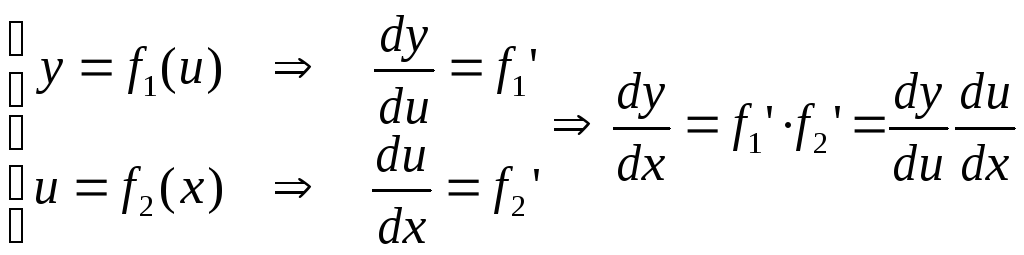2. у=f₁(f₂(f ₃(x)))

Совершенно аналогично представляются и рассчитываются и более громоздкие функции.

Производная неявной функции

Неявная функция включает в себя составляющие, которые содержат операции над у=f(x). Например, у² или и т.п. Рассмотрим выражение F=, гдеу=f(x). Подходя к нему как к сложной функции, запишем систему:

Это и есть правило дифференцирования неявной функции.

Пример: х²+у²=100

Следовательно, производная от данной неявной функции имеет вид:

2х+2у, откуда .

Производные высших порядков

Производная определяет, очевидно, некоторую новую функцию, которую, конечно, можно продифференцировать еще раз. По отношению к исходной функцииу=f(x) это будет уже вторая производная или. Ясно, что этот процесс можно продолжать и получать все более высокие производные. По-другому:

Пример: для у=sin x и т.д.

Только вторая производная имеет общефизический смысл - она характеризует “скорость изменения скорости” функции в точке, т.е. - ускорение.

Логарифмическое дифференцирование

Рассмотрим сложную функцию , где у=f(x). Запишем систему:

.

Выражение и называется логарифмической производной.

На практике очень часто приходится иметь дело с дифференцированием сложных степенных функций. Предварительное логарифмирование позволяет упростить эту задачу. Пример: .

Таким образом, .

Дифференциал функции

Вернемся к определению производной: С помощью свойства связи предела и бесконечно малой величины (см. главуПределы), запишем: или . Так как - бесконечно малая истремится к нулю, то вторым слагаемым можно пренебречь. Тогда первое слагаемоеи называетсядифференциалом функции у=f(х). Для того, чтобы подчеркнуть это определение, принято записывать Рассмотрим геометрический смысл дифференциала:

Дифференциалом функции у=f(х) первого порядка называется главная, линейная относительно приращения , часть приращения функции, равная произведению производной этой функции на приращение аргумента, обозначаемое в этом случае, какdx.

dy == tg  dx

Эквивалентность записи докажем и по-другому: пустьу=х, тогда

.

Отсюда и следует Кроме того, определение дифференциала обосновывает представление производной, как отношения: изdy=следует

Свойства дифференциала аналогичны свойствам производной:

1. dC= 0, C - постоянная (число).

2. d(Cy)= Cdy.

3. d(uv)= dudv.

4. d(uv)= v du+u dv.

5. .

Приведем обозначения для дифференциалов высших порядков: и т.д.

Формула для дифференциала используется в приближенных вычислениях. Действительно, из следует: , откуда . Чем меньше значение , тем точнее результат. К примеру, вычислим. Здесь и Тогда

или - практически точно.