Бесконечно малые (б.М.) и бесконечно большие (б.Б.) величины

Так как б.м. и б.б. часто встречаются в анализе, то сформулируем их свойства. Для удобства положим (х) - б.м., (х) - б.б. величины при ха (или х).

1. Если функция у=f(х) может быть представлена суммой постоянного числа А и б.м. величины (х), т.е. у=А+, то lim y = A и обратно, если lim y = A, то у=А+.

2. Сумма нескольких б.м. величин тоже является б.м. величиной.

3. Произведение б.м. величины на ограниченную функцию (или число) также является б.м. величиной.

4. Частное от деления б.м. величины на ненулевую ограниченную функцию (или число) является б.м. величиной.

5. Произведение б.б. величины на ограниченную функцию (или число) также является б.б. величиной.

6. Сумма б.б. величины и ограниченной функции (или числа) является б.б. величиной.

7. Частное от деления б.б. величины на ненулевую ограниченную функцию (или число) является б.б. величиной.

8. Величина, обратная б.м. величине, является б.б. величиной: (х)=; Величина, обратная б.б. величине, является б.м. величиной:(х)=.

Теоремы о пределах

Для того, чтобы вычислять пределы, разработан ряд удобных теорем, которые приведем без доказательств:

1. Предел постоянной величины (числа) равен этой постоянной: lim C=C.

2. Предел суммы равен сумме пределов: lim(u+v-w)=lim u+ lim v- lim w.

3. Предел произведения равен произведению пределов:

lim(uvw)=lim ulim vlim w.

4. Предел дроби равен частному пределов числителя и знаменателя при условии, что знаменатель - не б.м. величина: lim.

5. В неравенствах можно переходить к пределу, т.е., если u<v (или другой знак неравенства), то lim u<lim v.

Замечательные пределы

Ряд достаточно часто встречающихся в практике пределов по историческим причинам получил название замечательных. Приведем некоторые из них, встречающиеся в практических задачах:

1. 2., где е=2,718281828...

3. . 4. . 5. .

Вычисление пределов

1. Прямая подстановка: . Это - наиболее общий прием, который всегда используется первым: (х² – х + 1) = 4² – 4 + 1 = 13.

2. Упрощение функций. Если при прямой подстановке получается неопределенное выражение типов: , и некоторых других, то выделение общего множителя или приведение к замечательным пределам приводят к нужному результату:

==

==

В последнем примере учтено, что, если х0, то, очевидно, и 5х0 (свойство 3 в разделе 6.3).

Непрерывность и разрывы функции

Функция f(x) называется непрерывной в точке x₀ если она:

1. Определена в этой точке, т.е. существует f(x₀).

2. Имеет предел в этой точке А = .

3. Предел совпадает со значением функции А = f (x₀).

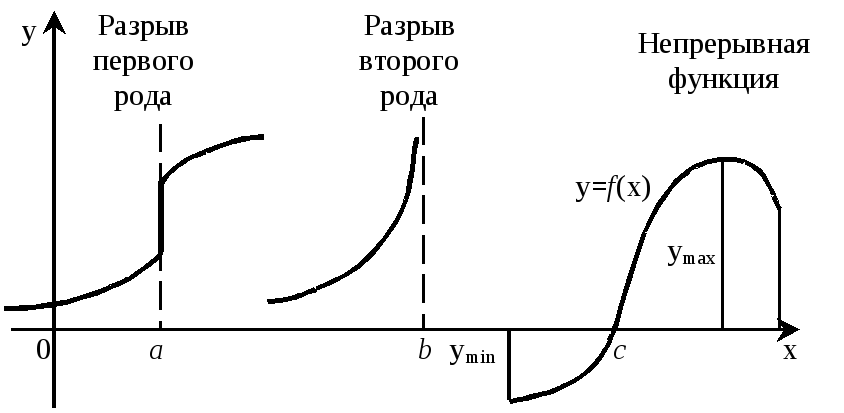
Если хотя бы одно из этих условий нарушено, то функция разрывная в точке x₀. Этот разрыв может быть конечен - скачок (разрыв первого рода), или бесконечен (второго рода).

Для функций, непрерывных в точке x₀ сумма f₁+f₂, произведение f₁f₂ и частное (приf₂0) также непрерывны в этой точке.

Если функция y= f₁(u) непрерывна в точке u₀, а функция u= f₂(x) непрерывна в точке f₂(x₀), то, при u₀= f₂(x₀), сложная функция f₁(f₂(x)) тоже непрерывна в этой точке, т.е. можно записать: .

Функция y= f(x) называется непрерывной на интервале axb, если она непрерывна в каждой точке этого интервала. При этом:

1. Она ограничена на этом интервале сверху и снизу (не может быть бесконечного значения).

2. Обязательно имеет минимальное и максимальное значения.

3. Если по концам интервала функция имеет разные знаки, то внутри интервала имеется хотя бы одна точка х=с, в которой f(с)=0 (корень функции).