12

Лекция 6

по дисциплине «Информатика и ИКТ»

ТЕМА 2 «ОРГАНИЗАЦИЯ И ФУНКЦИОНИРОВАНИЕ КОМПЬЮТЕРОВ»

Раздел 1. Принципы работы компьютера

Содержание:

1.1. Битовое и байтовое представление чисел. Системы счисления

1.2. Кодирование информации и её представление в памяти компьютера

1.3. Понятие алгоритма

1.4. Методы обработки данных. Элементарные методы (команды)

1.5. Информационные объекты. Свойства и примеры

1.1. Битовое и байтовое представление чисел. Системы счисления

Чтобы понять, как представляются числа в виде бит, проанализируем сначала представление чисел в хорошо всем знакомой десятичной системе счисления (строгое определение системы счисления дадим ниже). Запись 175 – состоит из 3-х символов – “1”, “7” и “5” записанных в строго определенном порядке (751 или 517 – это совсем другие числа). Эти символы называются цифрами и выбираются из фиксированного набора десяти цифр “0”, “1”, “3”, “4”, “5”, “6”, ”7”, “8”, “9”.

Способ записи чисел при помощи фиксированного набора символов (цифр) называется системой счисления. Если в записи числа важен порядок расположения цифр, то система счисления называется позиционной. Далее мы будем рассматривать только позиционные системы счисления.

Суть преобразования последовательности цифр в число в любой позиционной системе счисления заключается в соглашении о разрядах. Разряды нумеруются справа налево, начиная с 0, цифра стоящая в k-ом разряде означает количество единиц этого разряда.

Чтобы понять, что такое разряд, рассмотрим следующий пример интерпретации того же числа 175. Пусть у нас есть 175 каких-либо элементов, например, 175 яблок. Предположим, что у нас есть коробки фиксированных размеров, в которые мы можем эти яблоки упаковывать, причем, в самые маленькие коробки помещается ровно 10 яблок, в коробки побольше помещается ровно 10 маленьких коробок и т.д. Будем упаковывать яблоки в коробки следующим образом. Начнем укладывать яблоки в маленькие коробки, как только у нас наберется 10 маленьких коробок – уложим их в одну большую и т.д. В результате этого процесса у нас получится 1 заполненная большая коробка, 7 заполненных маленьких коробок и еще 5 оставшихся яблок. Это и есть значения десятичных разрядов. Наш результат можно записать в следующем виде: 175 = 1·10²+ 7·10+ 5.

Предположим теперь, что в маленькую коробку помещается не 10, а 8 яблок, а в большую не 10, а 8 маленьких коробок и т. д. Если мы проведем процесс упаковки яблок в эти коробки, то получится следующее. Т.к. полностью заполненная большая коробка должна включать 8 маленьких, т.е. 8·8 = 64 яблока, то 2 полностью заполненных больших коробки будут содержать 2·64 = 128 яблок, а для того, чтобы полностью заполнить 3 больших коробки потребовалось бы 3·64 = 192 яблока. Т.к. яблок у нас 175 < 192, то заполненных больших коробок будет 2. Оставшиеся 175 – 128 = 47 яблок упакуются в 5 маленьких коробок и еще останется 47 - 5·8 = 7 яблок. В результате получатся 2 больших коробки, 5 маленьких и еще 7 яблок. Процедура, которую мы проделали, соответствует представлению числа 175 в восьмеричной, системе счисления. Наш результат записывается так 175 = (257)₈ или 175 = 2·8²+ 5·8+ 7. Ясно, что в восьмеричной системе могут быть только 8 цифр: “0”, “1”, “2”, “3”, “4”, “5”, “6”, “7”.

Как видим, для представления числа 175 в десятичной, и в восьмеричной системах счисления необходимо 3 разряда (2 типа коробок + 1 разряд для оставшихся яблок).

Аналогично можно представить число 175 в двоичной системе счисления – для этого нужно упаковать яблоки в коробки с емкостями, последовательно увеличивающимися в 2 раза: в маленькую коробку должно помещаться 2 яблока, в коробку следующего размера – 2 маленьких коробки и т.д. При этом 3-х разрядов уже не хватит, необходимо будет использовать 8 разрядов:

175 = (10101111)₂ = 1·2⁷+0·2⁶+1·2⁵+0·2⁴+1·2³+1·2²+1·2¹+1.

Дадим теперь строгое определение системы счисления с основанием q.

Будем считать, что задана система счисления с основанием q, если задано натуральное число q > 1 и набор из q символов {e_i}, причем, каждому из символов e_i поставлено в соответствие численное значение 0 до q-1, так что между множеством символов {e_i} и множеством чисел {0, 1, 2, … q-1} установлено взаимнооднозначное соответствие. При этом q называется основанием системы счисления, а символы {e_i} - цифрами.

Любое натуральное число p при этом можно представить в виде

(1.3.1)

или в позиционной записи

(1.3.2).

Рациональные числа также могут быть представлены в виде (1.3.1), если использовать кроме положительных еще и отрицательные степени q, при этом в записи (1.3.2) появится разделитель (запятая или точка), отделяющий целую часть от дробной.

Несколько слов о соглашениях при позиционной записи чисел. Основание 10 опускается, поэтому вместо (187)₁₀ пишут просто 187. Вместо основания 16 часто используется значок “#”, т.е. #187 = (187)₁₆. Часто также основание опускается, когда из контекста ясно, какая именно система счисления используется.

Рассмотрим преобразование чисел из системы счисления с основанием q в десятичную систему счисления и обратно.

Перевод в десятичную систему дает формула (1.3.1), если значения e_i и q выражены в десятичной системе. Например,

Перевод числа десятичного числа p в систему счисления с основанием q производится несколько сложнее, т.к. необходимо вместо умножения на q использовать деление. Из выражения (1.3.1) следует, что деление нацело p/q дает в результате целое число и остаток e_0. Деление нацело p₁ на q дает и остаток e₂ и т.д. Таким образом, цифрами для представления числа p в системе счисления с основанием q являются остатки, получающиеся при последовательном делении нацело на q сначала числа p, потом результата деления p₁ и т.д. При записи числа эти остатки необходимо расположить справа налево.

Например, переведем число 483 в восьмеричную запись

Таким образом, 483 = (743)₈.

Рассмотрим теперь две основные системы счисления, используемые в компьютерных системах – двоичную и шестнадцатеричную.

В двоичной системе q = 2, e_i={0, 1}. Каждый двоичный разряд представляет 1 бит данных. Биты почти всегда группируются в байты по 8 бит, т.е. каждый байт состоит из 8 двоичных разрядов с номерами от 0 до 7. Младший (нулевой) разряд – самый правый. Перевод конкретного значения дискретной величины в набор бит сводится к переводу записи числа в двоичную систему счисления. Например, задача записи числа 175 в виде битовой последовательности решается следующим образом:

т.е. 175 = (10101111)₂. Битовая последовательность из 9 бит, представляющая число 175 будет выглядеть в виде схемы , где затемненными квадратиками обозначены биты, установленные в 1, а пустыми квадратиками – биты установленные в 0. Приведенная схема соответствует компьютерному представлению числа 175.

В шестнадцатеричной системе счисления q =16, поэтому должно быть 16 цифр. В качестве первых десяти цифр (от 0 до 9) можно использовать обычные десятичные цифры, но для последних шести (имеющих значения от 10 до 15) необходимо использовать какие-то дополнительные символы. В качестве таких символов используются первые 6 букв латинского алфавита A, B, C, D, E, F, при этом считается, что A=10, B=11, C=12, D=13, E=14, F=15. Таким образом, набор цифр шестнадцатеричной системы счисления e_i={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.

В шестнадцатеричной системе счисления очень удобно записывать значения байт, т.к. один байт всегда представляется двузначным шестнадцатеричным числом.

Приведем примеры перевода чисел из шестнадцатеричной системы в десятичную.

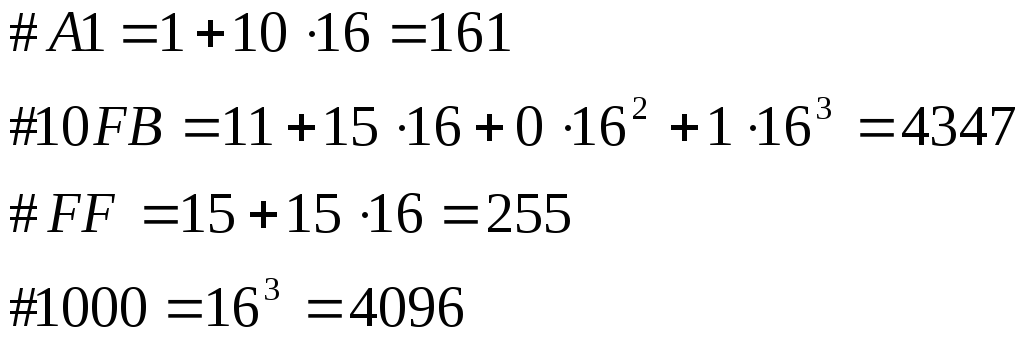
Примеры обратного перевода

В заключение отметим, что любой перевод чисел между четырьмя основными системами счисления – десятичной, восьмеричной, двоичной и шестнадцатеричной можно легко осуществлять при помощи стандартной программы Калькулятор, входящей в состав операционной системы Windows. Для этого Калькулятор нужно перевести в инженерный вид (Вид/Инженерный), после чего точечным переключателем выбрать исходную систему счисления (Dec-десятичная, Hex-шестнадцатеричная, Bin-двоичная, Oct-восьмеричная) и ввести число. Затем изменить переключателем систему счисления – число окажется записанным в новой системе.