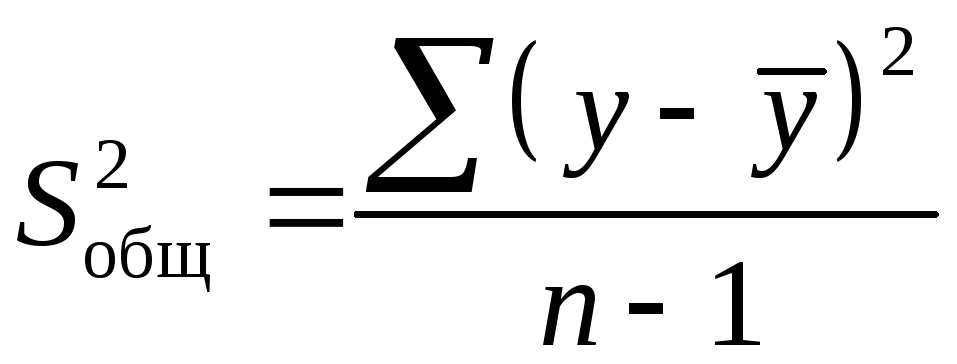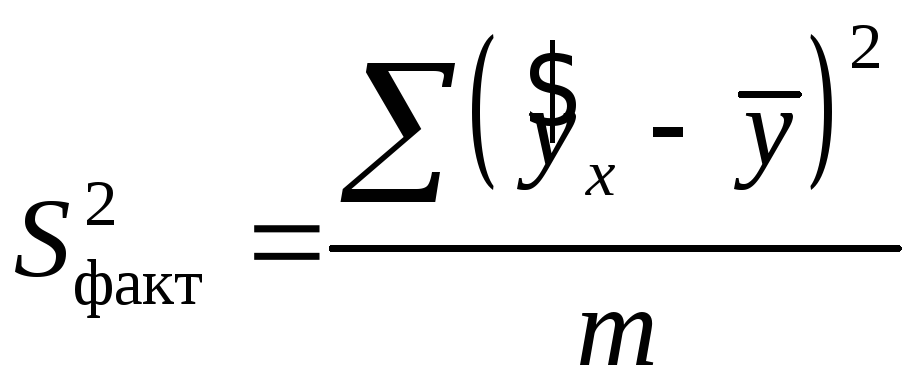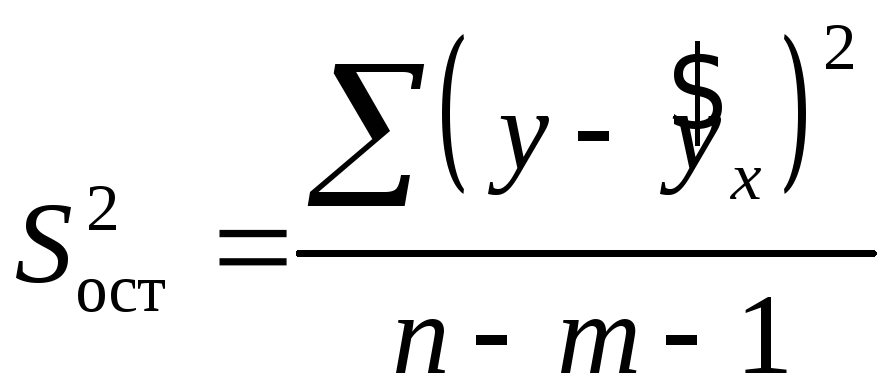- •Определение эконометрики. Метод эконометрики
- •Эконометрический метод и этапы эконометрического исследования.
- •Парная регрессия. Способы задания уравнения парной регрессии.
- •Линейная модель парной регрессии. Смысл и оценка параметров.
- •Оценка существенности уравнения в целом на основе дисперсионного анализа (-критерий фишера).
- •Оценка существенности отдельных параметров регрессии (-критерий стьюдента).
- •Прогноз по линейному уравнению регрессии. Средняя ошибка аппроксимации.
- •Нелинейная регрессия. Классы нелинейных регрессий. Оценка нелинейной регрессии в целом
- •Регрессии нелинейные относительно включенных в анализ объясняющих переменных.
- •Регрессии нелинейные по оцениваемым параметрам.
- •Коэффициенты эластичности для разных видов регрессионных моделей.
- •Корреляция и-критерий фишера для нелинейной регрессии.
- •Отбор факторов при построении уравнения множественной регрессии.
- •Отбор факторов на основе корреляционного анализа. Коллинеарность
- •Отбор факторов на основе корреляционного анализа. Мультиколлинеарность
- •Оценка параметров уравнения множественной регрессии. Стандартизированная форма уравнения множественной регрессии
- •Эластичность в множестенной регрессии.
- •Множественная корреляция.
- •Частные коэффициенты корреляции.
- •-Критерий фишера и частный-критерий фишера для уравнения множественной регрессии.
- •-Критерий стьюдента для уравнения множественной регрессии.
Оценка существенности уравнения в целом на основе дисперсионного анализа (-критерий фишера).
Оценка значимости уравнения регрессии
в целом производится на основе
![]() -критерия
Фишера, которому предшествует дисперсионный
анализ. В математической статистике
дисперсионный анализ рассматривается
как самостоятельный инструмент
статистического анализа. В эконометрике
он применяется как вспомогательное
средство для изучения качества
регрессионной модели.
-критерия
Фишера, которому предшествует дисперсионный
анализ. В математической статистике
дисперсионный анализ рассматривается
как самостоятельный инструмент
статистического анализа. В эконометрике
он применяется как вспомогательное
средство для изучения качества
регрессионной модели.
Согласно основной идее дисперсионного
анализа, общая сумма квадратов отклонений
переменной
![]() от среднего значения
от среднего значения![]() раскладывается на две части – «объясненную»
и «необъясненную»:
раскладывается на две части – «объясненную»
и «необъясненную»:
![]() ,
,
где
![]() – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;![]() – сумма квадратов отклонений, объясненная
регрессией (или факторная сумма квадратов
отклонений);
– сумма квадратов отклонений, объясненная
регрессией (или факторная сумма квадратов
отклонений);![]() – остаточная сумма квадратов отклонений,
характеризующая влияние неучтенных в
модели факторов.
– остаточная сумма квадратов отклонений,
характеризующая влияние неучтенных в
модели факторов.
Схема дисперсионного анализа имеет
вид, представленный в таблице 1.1 (![]() – число наблюдений,
– число наблюдений,![]() – число параметров при переменной
– число параметров при переменной![]() ).
).
Таблица 1.1
|
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Дисперсия на одну степень свободы |
|
Общая |
|
|
|
|
Факторная |
|
|
|
|
Остаточная |
|
|
|
Определение дисперсии на одну степень
свободы приводит дисперсии к сравнимому
виду. Сопоставляя факторную и остаточную
дисперсии в расчете на одну степень
свободы, получим величину
![]() -критерия
Фишера:
-критерия
Фишера:
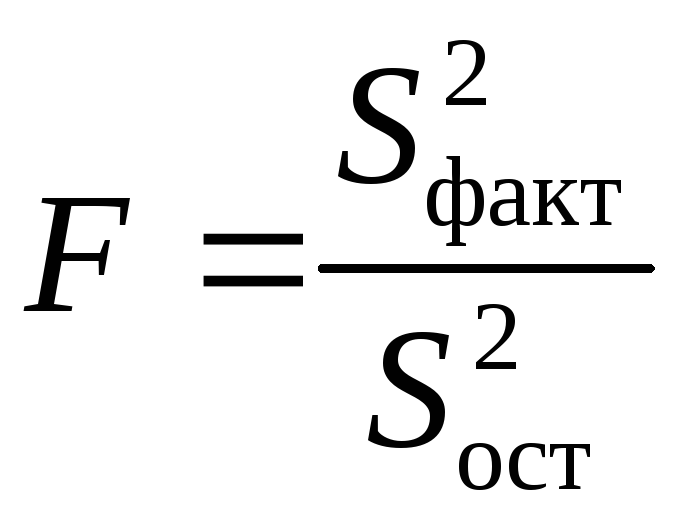 .
(1.9)
.
(1.9)
Фактическое значение
![]() -критерия
Фишера (1.9) сравнивается с табличным
значением
-критерия
Фишера (1.9) сравнивается с табличным
значением![]() при уровне значимости
при уровне значимости![]() и степенях свободы
и степенях свободы![]() и
и![]() .
При этом, если фактическое значение
.
При этом, если фактическое значение![]() -критерия
больше табличного, то признается
статистическая значимость уравнения
в целом.
-критерия
больше табличного, то признается
статистическая значимость уравнения
в целом.
Для парной линейной регрессии
![]() ,
поэтому
,
поэтому
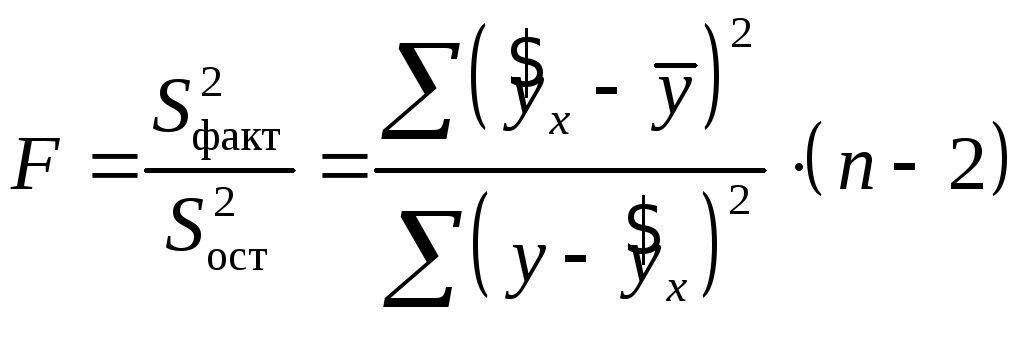 .
(1.10)
.
(1.10)
Величина
![]() -критерия
связана с коэффициентом детерминации
-критерия
связана с коэффициентом детерминации![]() ,
и ее можно рассчитать по следующей
формуле:
,
и ее можно рассчитать по следующей
формуле:
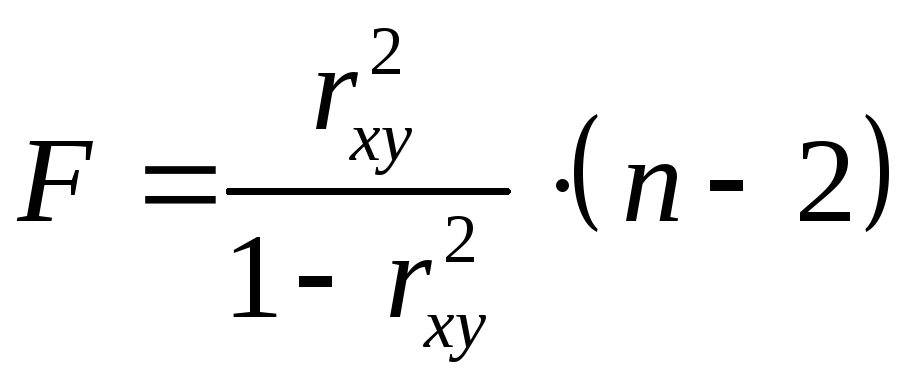 .
(1.11)
.
(1.11)
Оценка существенности отдельных параметров регрессии (-критерий стьюдента).
В парной линейной регрессии оценивается
значимость не только уравнения в целом,
но и отдельных его параметров. С этой
целью по каждому из параметров определяется
его стандартная ошибка:
![]() и
и![]() .
.
Стандартная ошибка коэффициента регрессии определяется по формуле:
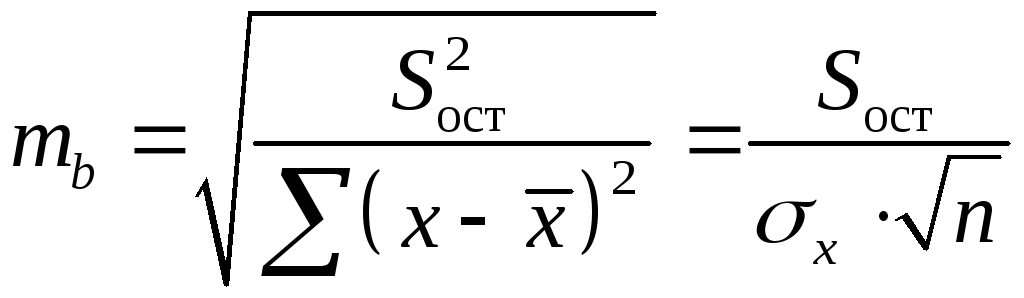 ,
(1.12)
,
(1.12)
где
 – остаточная дисперсия на одну степень
свободы.
– остаточная дисперсия на одну степень
свободы.
Величина стандартной ошибки совместно
с
![]() -распределением
Стьюдента при
-распределением
Стьюдента при![]() степенях свободы применяется для
проверки существенности коэффициента
регрессии и для расчета его доверительного
интервала.
степенях свободы применяется для
проверки существенности коэффициента
регрессии и для расчета его доверительного
интервала.
Для оценки существенности коэффициента
регрессии его величина сравнивается с
его стандартной ошибкой, т.е. определяется
фактическое значение
![]() -критерия
Стьюдента:
-критерия
Стьюдента: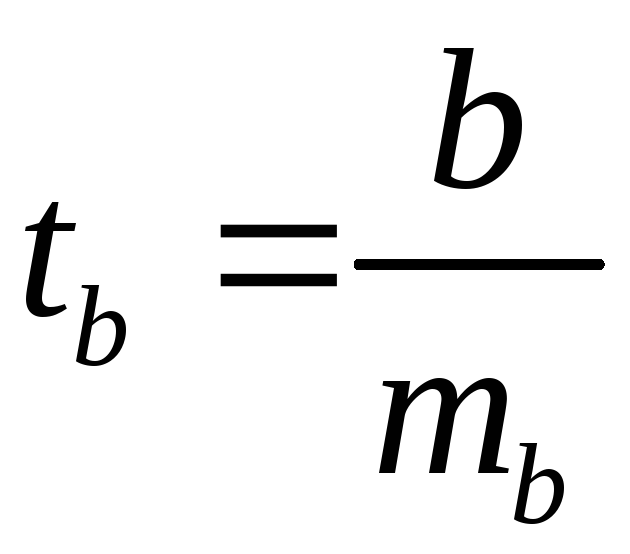 которое затем сравнивается с табличным
значением при определенном уровне
значимости
которое затем сравнивается с табличным
значением при определенном уровне
значимости![]() и числе степеней свободы
и числе степеней свободы![]() .
Доверительный интервал для коэффициента
регрессии определяется как
.
Доверительный интервал для коэффициента
регрессии определяется как![]() .
Поскольку знак коэффициента регрессии
указывает на рост результативного
признака
.
Поскольку знак коэффициента регрессии
указывает на рост результативного
признака![]() при увеличении признака-фактора
при увеличении признака-фактора![]() (
(![]() ),
уменьшение результативного признака
при увеличении признака-фактора (
),
уменьшение результативного признака
при увеличении признака-фактора (![]() )
или его независимость от независимой
переменной (
)
или его независимость от независимой
переменной (![]() )
(см. рис. 1.3), то границы доверительного
интервала для коэффициента регрессии
не должны содержать противоречивых
результатов, например,
)
(см. рис. 1.3), то границы доверительного
интервала для коэффициента регрессии
не должны содержать противоречивых
результатов, например,![]() .
Такого рода запись указывает, что
истинное значение коэффициента регрессии
одновременно содержит положительные
и отрицательные величины и даже ноль,
чего не может быть.
.
Такого рода запись указывает, что
истинное значение коэффициента регрессии
одновременно содержит положительные
и отрицательные величины и даже ноль,
чего не может быть.

Рис. 1.3.
Наклон
линии регрессии в зависимости от значения
параметра
![]() .
.
Стандартная ошибка параметра
![]() определяется по формуле:
определяется по формуле:
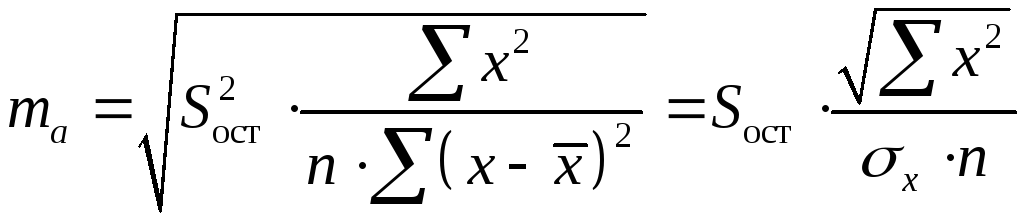 .
(1.13)
.
(1.13)
Процедура оценивания существенности
данного параметра не отличается от
рассмотренной выше для коэффициента
регрессии. Вычисляется
![]() -критерий:
-критерий: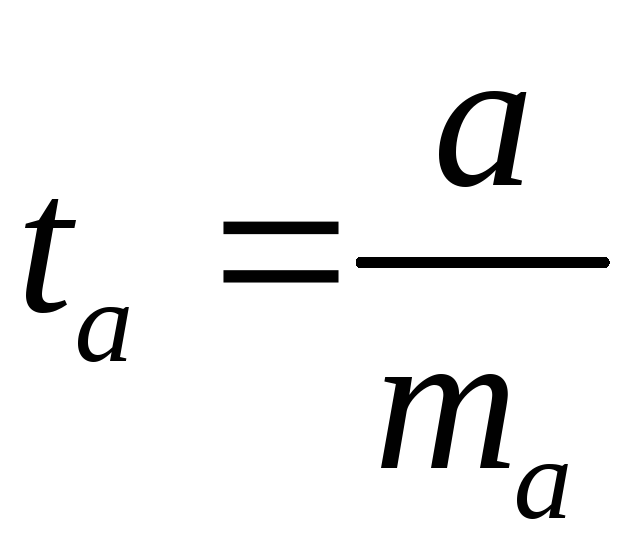 ,
его величина сравнивается с табличным
значением при
,
его величина сравнивается с табличным
значением при![]() степенях свободы.
степенях свободы.
Значимость линейного коэффициента
корреляции проверяется на основе
величины ошибки коэффициента корреляции
![]() :
:
 .
(1.14)
.
(1.14)
Фактическое значение
![]() -критерия
Стьюдента определяется как
-критерия
Стьюдента определяется как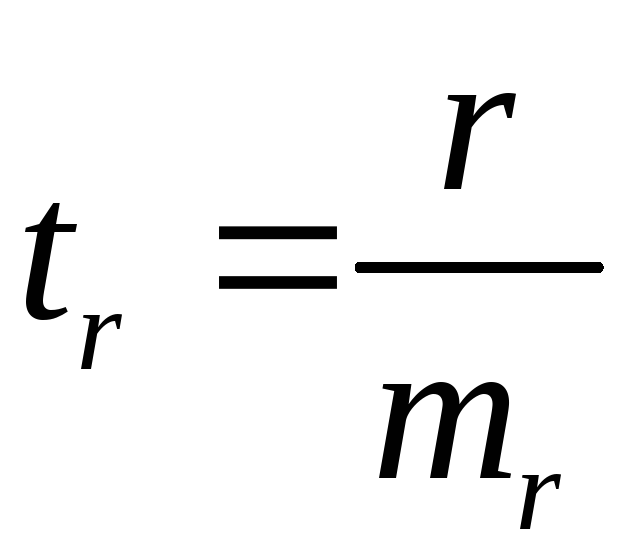 .
.
Существует связь между
![]() -критерием
Стьюдента и
-критерием
Стьюдента и![]() -критерием
Фишера:
-критерием
Фишера:
![]() .
(1.15)
.
(1.15)
(1.16)