13.3. Алгоритмы работы с деревьями

В приведенных ниже алгоритмах предполагается, что узел (элемент) дерева декларирован сл

Type

PNode = ^TNode;

TNode = record

Data : integer; {информационное поле}

left,right : PNode;

end;

едующей записью:

А1. Вычисление суммы значений информационных полей элементов

Алгоритм реализован в виде функции, возвращающей значение суммы информационных полей всех элементов. Тривиальным считается случай, когда очередной узел – пустой, и, следовательно, не имеет информационного поля.

function Sum(Root : PNode) : integer;

begin

if Root=Nil then {узел - пустой}

Sum := 0

else

Sum := Root^.Data + Sum(Root^.left)

+ Sum(Root^.right);

{end if}

end;

Для нетривиального случая результат вычисляется как значение информационного элемента в корне (Root^.Data) плюс суммы информационных полей левого и правого поддеревьев.

А выражение Sum(Root^.left)представляет собой рекурсивный вызов левого поддерева для данного корня Root.

А2. Подсчет количества узлов в бинарном дереве

function NumElem(Tree:PNode):integer;

begin

if Tree = Nil then

NumElem := 0

else

NumElem := NumElem(Tree^.left)

+ NumElem(Tree^.right) + 1;

{end if}

end;

А3. Подсчет количества листьев бинарного дерева

function Number(Tree:PNode):integer;

begin

if Tree = Nil then

Number := 0 {дерево пустое – листов нет}

else if (Tree^.left=Nil) and (Tree^.right=Nil) then

Number := 1 {дерево состоит из одного узла - листа}

else

Number := Number(Tree^.left) + Number(Tree^.right);

{end if}

end;

Анализ приведенных алгоритмов показывает, что для получения ответа в них производится просмотр всех узлов дерева. Ниже будут приведены алгоритмы, в которых порядок обхода узлов дерева отличается. И в зависимости от порядка обхода узлов бинарного упорядоченного дерева, можно получить различные результаты, не меняя их размещения.

Примечание: Просмотр используется не сам по себе, а для обработки элементов дерева, а просмотр сам по себе обеспечивает только некоторый порядок выбора элементов дерева для обработки. В приводимых ниже примерах обработка не определяется; показывается только место, в котором предлагается выполнить обработку текущего

А4. Алгоритмы просмотра дерева

Самой интересной особенностью обработки бинарных деревьев является та, что при изменении порядка просмотра дерева, не изменяя его структуры, можно обеспечить разные последовательности содержащейся в нем информации. В принципе возможны всего четыре варианта просмотра: слева-направо, справа-налева, сверху-вниз и снизу-вверх. Прежде чем увидеть, к каким результатам это может привести, приведем их.

а. Просмотр дерева слева – направо

procedure ViewLR(Root:PNode); {LR -> Left – Right }

begin

if Root<>Nil then

begin

ViewLR(Root^. left); {просмотр левого поддерева}

{Операция обработки корневого элемента –

вывод на печать, в файл и др.}

ViewLR(Root^.right); { просмотр правого поддерева }

end;

end;

б. Просмотр справа налево

procedure ViewRL(Root:PNode); {LR -> Right – Left}

begin

if Root<>Nil then

begin

ViewRL(Root^.right); {просмотр правого поддерева}

{Операция обработки корневого элемента –

вывод на печать, в файл и др.}

ViewRL(Root^.left); { просмотр левого поддерева }

end;

end;

в. Просмотр сверху – вниз

procedure ViewTD(Root:PNode); {TD –> Top-Down}

begin

if Root<>Nil then

begin

{Операция обработки корневого элемента –

вывод на печать, в файл и др.}

ViewTD(Root^.left); {просмотр левого поддерева}

ViewTD(Root^.right); { просмотр правого поддерева }

end;

end;

г. Просмотр снизу-вверх

procedure ViewDT(Root:PNode); {DT –> Down - Top}

begin

if Root<>Nil then

begin

ViewDT(Root^.left); {просмотр левого поддерева}

ViewDT(Root^.right); { просмотр правого поддерева }

{Операция обработки корневого элемента –

вывод на печать, в файл и др.}

end;

end;

Пример 1. Рассмотрим результаты просмотра для приведенных алгоритмов, при условии, что обработка корневого элемента сводится к выводу значения его информационного поля, а дерево в этот момент имеет следующие узлы:

Результаты просмотра:

Алгоритм «Слева направо»	1, 3, 7, 10, 70, 96, 98
Алгоритм «Справа налево»	98, 96, 70, 10, 7, 3, 1
Алгоритм «Сверху вниз»	10, 3, 1, 7, 96, 70, 98

Из приведенной таблицы видно, что, просто изменяя порядок просмотра дерева (слева-направо и справа-налево), можно получить отсортированные по возрастанию или по убыванию числа.

Пример 2. Пусть в узлах дерева расположены элементы арифметического выражения:

Р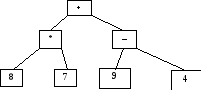езультаты просмотра:

«Слева направо»	8 * 7 + 9 – 4	инфиксная форма записи выражения
«Сверху вниз»	+ * 8 7 – 9 4	префиксная форма записи выражения
«Снизу вверх»	8 7 * 9 4 – +	постфиксная форма записи выражения

A

{ Определить существование значения SearchValue

и вернуть указатель на элемент, содержащий его,

или вернуть Nil, если элемент не найден}

function Search(SearchValue:integer;Root:PNode):PNode;

begin

if (Root=Nil) or (Root^.Data=SearchValue) then

Search := Root

else if (Root^.Data > SearchValue) then

Search := Search(SearchValue,Root^.left)

else

Search := Search(SearchValue,Root^.right);

{end if}

end;

5. Поиск элемента в двоичном упорядоченном дереве

Вывод. Тексты приведенных алгоритмов очень компактны и просты в понимании.

В заключение отметим, что рекурсивные алгоритмы широко используются в базах данных и при построении компиляторов, в частности для проверки правильности записи арифметических выражений, синтаксис которых задается с помощью синтаксических диаграмм.

Для закрепления материала предлагается решить следующую задачу:

Данные о студентах содержат фамилию и три оценки, полученные на экзаменах. Занести их с клавиатуры или из текстового файла в бинарное дерево поиска, упорядоченное по значению средней оценки. Затем вывести на экран список студентов, упорядоченный по убыванию средней оценки. Кроме фамилий вывести все три оценки и их среднее значение с точностью до одного знака после запятой.