153

13. Динамические структуры данных типа «дерево»

13.1. Определение дерева и способы представления в программе

Структуру данных типа «дерево» можно определить следующим образом:

Древовидная структура с базовым типом Т это либо пустая структура, либо узел типа Т, с которым связано конечное число древовидных структур с базовым типом Т, называемых поддеревьями. Рассмотренная ранее структура данных типа «линейный разомкнутый список» может рассматриваться как вырожденное дерево.

Д

ерево можно изобразить несколькими способами. Наиболее наглядный способ – в виде графа. В этом случае граф выглядит как перевернутое дерево (отсюда и название структуры – «дерево»):

Приведем несколько определений, связанных со структурами данного вида.

Верхний узел дерева называют узлом уровня 1 или корнем дерева. Далее номера уровней возрастают. Максимальный уровень дерева называют также глубиной или высотой дерева. В приведенном выше графе глубина дерева (максимальный уровень узлов дерева) равна четырем.

Два узла У (уровня k) и Х (уровня k+1) определяют следующим образом:

узел У считается предком узла Х, а узел Х – потомком узла У.

Если узел не имеет потомков, он называется терминальным узлом или листом. Все прочие узлы называют внутренними узлами.

Упорядоченное дерево – дерево, у которого ветви каждого узла упорядочены.

Приведенные ниже графы двух упорядоченных деревьев не идентичны (отличаются).

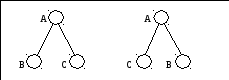
Дерево, каждый узел которого имеет не более двух потомков, называют бинарным. По аналогии с этим троичное дерево – дерево, узлы которого не имеют более трех потомков. А дерево, отдельные узлы которого имеют более трех потомков, называют сильно ветвящимся.

Упорядоченное бинарное дерево – конечное множество элементов (узлов), каждый из которых либо пуст, либо состоит из корня (узла), связанного с двумя различными бинарными деревьями, называемыми левым и правым поддеревьями корня.

Н

A

B C

D E F

G H I

иже приведен пример бинарного дерева:

Здесь:

A – корень дерева

B – корень левого поддерева дерева А

C – корень правого поддерева дерева А

D, G, H, I – листья

B – левый потомок дерева A

C – правый потомок дерева A

В программе на Паскале дерево представляется в виде иерархического списка, элемент которого (изображающий узел дерева) можно рассматривать как структуру следующего вида:

Info
Child	Next

Здесь

Info – поле, содержащее полезную информацию

Child – ссылка на элемент-потомок

Next– ссылка на элемент того же уровня (на элемент, являющийсябратомданного).

Ниже приведен пример упорядоченного дерева в виде графа и в виде иерархического списка:

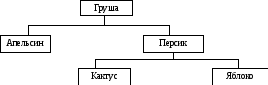
Это же дерево в программе можно представлено в виде следующей структуры:

Бинарные деревья (как упорядоченные, так и нет) широко используются в программировании. По этой причине мы сосредоточимся в основном на рассмотрении процедур работы с ними.

Для описания узла бинарного дерева в программе введем тип, имеющий вид следующей записи:

Type

PNode = ^TNode;

TNode = record

Info : string; {поле данных}

Left,Right : PNode; {указатели на левое и

правое поддеревья}

end;

Приведем несколько процедур, иллюстрирующих работу с деревьями.

П

{ Создание нового узла со значением информационного поля X.

Возвращается указатель на новый узел}

function NewNode(X:string):PNode;

var

P : PNode;

begin

New(P);

P^.Info := X;

P^.Left := Nil;

P^.Roght := Nil;

NewNode := P;

end;

ример 1. Процедура создания нового узла.

Пример2. Процедура создания потомка (поддерева).

{Процедура создания левого потомка для узла P} procedure SetLeft(P:PNode; X:string);

begin

P^.Left := NewNode(X);

end;

Пример 3. Создание бинарного дерева:

• данные (целые числа) заносятся с клавиатуры;

• дубликаты не включаются (но выводятся на экран);

• признаком окончания ввода является ввод числа 0;

• результат – бинарное упорядоченное дерево.

Примечание. В связи с ограниченными размерами страницы пособия текст программы разделен на две части.

Program BuildTree;

Type

PNode = ^TNode;

TNode = record

key : integer;

left,right : PNode;

end;

var

Root:PNode; {корень дерева}

NewData:PNode;{новый узел}

n:integer;

Продолжение текста программы смотрите на следующей странице.

procedure Add(NewData:PNode;var Root:PNode);

begin

if Root=Nil then {дерево пустое}

Root := NewData

else begin

if NewData^.key < Root^.key then

Add(NewData,Root^.left)

else if NewData^.key > Root^.key then

Add(NewData,Root^.right)

else begin {дубликат}

writeln(’ Дубликат ’, NewData^.key );

Dispose(NewData);

end;

end;

end; {Add}

begin {main program}

Root := Nil; {инициализировать пустое дерево}

repeat

write(’Введите число : ’,n);

readln(n);

if n<>0 then begin

NewData := NewNode(n); {функция создания узла

приведена выше}

Add(NewData,Root);

end;

until n=0;

. . .{здесь можно поместить операторы, в которых

созданное дерево используется для решения

конкретной задачи}

end.