3.6. Методика расчетов тепловых режимов рэс

Рассматриваемая ниже методика может быть распространена на большинство одноблочных конструкций РЭС с последовательно-составными тепловыми схемами (герметичные блоки) и некоторые конструкции с разветвленными тепловыми схемами (вентилируемые аппараты).

Расчет теплового режима может быть проведен для реально существующего аппарата или для разрабатываемого изделия, существующего в чертежах. Для получения алгоритма расчета теплового режима аппарата нужно провести следующие мероприятия:

1. Анализируются физические процессы в аппарате, приводящие к переносу тепловой энергии из аппарата в окружающую среду. На основании анализа составляется тепловая модель аппарата.

2. По тепловой модели составляется тепловая схема, учитывающая все тонкости переноса тепловой мощности. При любом изменении в конструкции или условий эксплуатации на тепловой схеме должен присутствовать элемент, реагирующий на эти изменения. Каждый элемент тепловой схемы должен иметь четкое математическое описание. В разделе 4.1 по этой схеме проведены указанные мероприятия, в результате чего получена точная тепловая схема герметичного блока с крупными деталями на шасси (рис. 4.1.3).

Так как мощность, выделяющаяся в нагретой зоне, без потерь проходит через кожух и рассеивается им в окружающей среде, особенности расчетов рассмотрим на участке кожух-среда.

Если известна температура , то каждая из проводимостей на рис. 3.6.1 рассчитывается в уже рассмотренном ранее порядке, затем рассчитывается проводимостьгдеi– поверхности кожуха верх, бок, дно. Далее по формуле Ньютона рассчитывается мощность, рассеиваемая в окружающую среду

. (3.6.1)

Эту процедуру условно можно назвать как решение прямой теплотехнической задачи, т.е. расчет мощности по известной температуре поверхности.

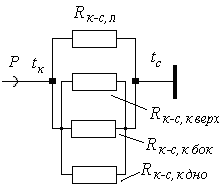
Рис. 3.6.1. Тепловая схема герметичного блока участка

кожух-среда

На практике чаще приходится рассчитывать температуру поверхности по известной подводимой мощности и эту процедуру также условно можно назвать как решение обратной теплотехнической задачи. Так как коэффициент теплоотдачи зависит от температуры поверхности, то прямое использование формулы Ньютона невозможно, так как нельзя рассчитать его, если неизвестна температура поверхности. Решать обратную теплотехническую задачу можно методом тепловой характеристики и методом последовательных приближений.

При использовании метода тепловой характеристики задаются двумя значениями температуры поверхности и. Для этих температур по формуле Ньютона рассчитываются мощностии. Так как при перегревемощность, уходящая с поверхности, будет равна нулю, то по трем точкам строится тепловая характеристика (рис. 3.6.2). Наложив на эту характеристику заданную мощность , получают соответствующий этой мощности перегрев поверхности. Расчеты будут более точными, если заданная мощность будет находиться в промежутке…. Поэтому после первого расчета проводят коррекцию величины.

Рис. 3.6.2. Расчет методом тепловой характеристики

Расчет методом последовательных приближений может осуществляться с автоматическим схождением процесса вычислений или с помощью заложенных в алгоритм вычислений программных решений.

Автоматическое схождение вычислений основано на нелинейности тепловой характеристики. Задаются перегревом поверхности первого приближения , вычисляют. Тогда формула (3.6.1) может быть записана в виде. Перегрев второго приближениябудет равен.

Так как расчетная мощность остается постоянной, то истинная величина будет находиться в диапазоне перегревов…. Необходимость продолжения вычислений оценивают по величине разброса температур

. (3.6.2)

Если разброс больше допустимой величины (), принимают=и повторяют описанный процесс вычислений для нового значения температуры. Расчеты прекращают, когда наступает условие. Динамика изменения числовых величин от цикла к циклу представлена на рис. 3.6.3. Разброс величин () уменьшается, причем величинавсегда будет находится внутри диапазона.

Рис. 3.6.3. Расчет методом последовательных приближений

Автоматического схождения процесса вычислений очень часто реализовать нельзя, например, в случае конструкций РЭС с разветвленными тепловыми схемами. В этом случае в алгоритме вычислений надо закладывать процедуру принудительной коррекции температуры первого приближения. При расчете задаются температурными границами расчетной температуры и. Они могут выбираться произвольно, например, ‑50 ^ОС и +100 ^ОС. Первый цикл вычислений проводят для температуры. В результате вычислений получаем величину рассеиваемой поверхностью мощности. Если>, то считают, что=, в противном случае=. Далее повторяют вычисления для температурыв новых температурных границах. С каждым циклом вычислений температурный диапазонбудет уменьшаться, а решение об окончании процесса вычислений принимают по величине разброса температурили по расхождению мощностейи. Следует отметить, что процесс схождения при описанном алгоритме более длительный по сравнению с использованием автосхождения. При использовании ЭВМ длительность вычислений особой роли не играет, но если нужно обучить тонкостям расчетов студентов, то программу следует упростить настолько, чтобы особенности расчетов можно было усвоить за 1-2 цикла, при этом степень упрощения следует обязательно оговорить.