2.1.2.1. Коэффициент теплоотдачи неограниченных цилиндров

Эта ситуация соответствует ламинарному режиму движения жидкости. Под неограниченными цилиндрами понимаются такие цилиндры, у которых длина во много раз больше диаметра (l>>d): выводы радиодеталей, некоторые типы резисторов, провода и т.д. Так как у нагретой поверхности не наблюдается вихреобразное движение, то определяющим размером считают диаметр проводника. Для ламинарного режима движения жидкости произведение критериев лежит в пределах ,n= 1/8,С = 1,18.

Подставляя n, C, , в выражение (2.1.6), получают выражение коэффициента теплоотдачи как функцию температуры и определяющего размера

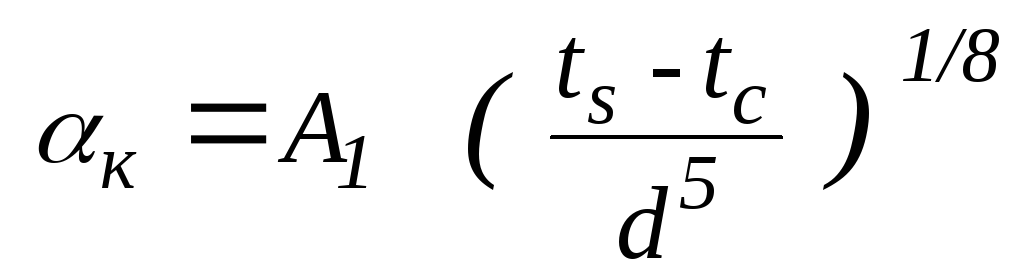, (2.1.7)

где А₁- коэффициент, в который вошли все теплофизические параметры теплоносителя;d- определяющий размер (диаметр цилиндра), [м].

Коэффициент А₁, как это следует из преобразования критериального уравнения, равен

. (2.1.8)

Его размерность равна . КоэффициентА₁рассчитан и приведен в виде таблицы [9] для различных температур.

2.1.2.2. Коэффициент теплоотдачи плоской (цилиндрической) поверхности

Когда плоская (цилиндрическая) поверхность (стенка кожуха блока, поверхность радиатора и т.д.) находится в неограничен-ном пространстве, т.е. вблизи нее нет тел, влияющих на процесс теплообмена, коэффициент теплоотдачи можно определить аналогичным предыдущему случаю преобразованием критериального уравнения (2.1.6).

Когда произведение лежит в пределах (500…2·10⁷), имеемС = 0,54 иn=1/4, т.е. теплообмен конвекцией подчиняется закону 1/4 степени. В этом случае после преобразования получают

. (2.1.9)

Аналогично для закона 1/3получают

, (2.1.10)

где коэффициенты А₂в уравнении (2.1.9) иА₃в уравнении (2.1.10), учитывающие теплофизические параметры среды, как следует из преобразования критериального уравнения, равны

, Вт / м^7/4К^5/4,(2.1.11)

, Вт / м²К^4/3.(2.1.12)

Значение этих коэффициентов для различных температур расcчитаны и даются в таблицах [9].

Коэффициент ориентации Nв уравнениях (2.1.9) и (2.1.10) учитывает неодинаковые условия теплообмена различно ориентированных поверхностей. При расчетах используют эмпирически подобранные значения коэффициента ориентации:N= 1 для вертикально ориентированной поверхности,N= 1,3 для горизонтально ориентированной поверхности, обращенной нагретой стороной вверх, ,N=0,7 для горизонтальной поверхности, обращенной нагретой стороной вниз [9].

Закон теплообмена для плоской или цилиндрической поверхности, не вычисляя произведения , можно определить из неравенства, предложенного в [9]:

, (2.1.13)

где L- определяющий размер, [м].

Если неравенство выполняется, теплообмен подчиняется закону 1/4 степени, в противном случае имеет место теплообмен по закону 1/3 степени.

2.1.2.3. Коэффициент теплопередачи между двумя поверхностями

В рассмотренных выше случаях выражения для конвективных коэффициентов теплоотдачи получены в предположении, что нагретое тело находится в неограниченном пространстве: жидкость, нагреваясь у поверхности тела за счет конвекции, уносится в окружающую среду, охлаждение ее протекает где-то вдали и не влияет на процесс теплообмена.

В РЭС наблюдаются ситуации, когда жидкость после нагрева остается вблизи источника тепла, что влияет на тепловой режим РЭС. Например, в РЭС с герметичным кожухом воздух нагревается ЭРЭ. Полученное тепло воздух должен передать кожуху, поэтому температура воздуха внутри РЭС будет выше температуры кожуха и ниже температуры ЭРЭ. Анализ тепловых процессов указанной ситуации проведен с помощью так называемых прослоек [9]. Под прослойкой понимают модель, в которой тепло передается от более нагретой поверхности к менее нагретой через зазор между этими поверхностями. При этом считается, что жидкость не уходит за пределы зазора, что предполагает наличие дополнительных ограничивающих поверхностей, причем эти поверхности не поглощают тепло.

В прослойках процесс теплообмена принято рассматривать как процесс передачи тепла от одной поверхности к другой за счет некоторой эквивалентной теплопроводности средыλ_э, заключенной между этими поверхностями. Другими словами, полагается, что прослойка между поверхностями представляет некоторую среду с коэффициентом теплопроводностиλ_э(рис. 2.1.2).

Рис. 2.1.2.Прослойка с эквивалентной теплопроводностью

Приняв поверхности изотермическими, тепловая мощность, переносимая кондукцией от одной поверхности к другой через такую прослойку, в соответствии с (2.3.12) и (2.3.13), будет равна

, (2.1.14)

где t₁, t₂-температуры поверхностей;δиS- толщина прослойки и площадь поверхности.

Введя понятие конвективно-кондуктивного коэффициента теплопередачи , получим выражение, аналогичное закону Ньютона

. (2.1.15)

Если теплообмен идет только за счет теплопроводности жидкости, то , где - теплопроводность жидкости при температуре . Наличие в прослойке конвективных процессов увеличивает интенсивность теплообмена, поэтому выражение для конвективно-кондуктивного коэффициента теплопередачи записывают в виде

, (2.1.16)

где - коэффициент конвекции, показывающий, во сколько раз конвективные процессы увеличивают интенсивность теплообмена по сравнению с теплообменом только за счет теплопроводности жидкости.

В конечном итоге при определении тепловой мощности Р задача сводится к определению коэффициента теплопередачи.

Прослойки можно условно разделить на две группы: неограниченные, у которых зазор значительно меньше геометрических размеров поверхностейl₁ и l₂, и ограниченные, у них зазор соизмерим с размерамиl₁ и l₂.

Рис. 2.1.3.Неограниченная (а) и ограниченная (б) прослойки

Если от размеров l₁ и l₂перейти к эквивалентной величинеl=( l₁·l₂ ) ^0,5, то прослойка считается неограниченной, если величина находится в пределах 0 <0,2. Для ограниченных прослоек величина лежит в пределах 0,2 <0,8 [9].