9. Интенсификация теплообмена в рэс. Радиаторы и их расчет

Одним из способов интенсификации теплообмена радиоэлектронных аппаратов является увеличение площади теплоотдающей поверхности за счет оребрения. С этой целью стенки кожухов аппаратов, аноды мощных ламп, корпуса других радиоэлектронных устройств выполняются в форме радиаторов, радиаторы находят широкое применение для отвода тепла от мощных полупроводниковых приборов и других ЭРЭ.

Известно большое количество конструкций радиаторов –плоские одно- и двусторонние оребренные, радиально оребренные, штыревые, дисковые, пластинчатые и т.д. Однако для всех их справедливы основные закономерности процесса теплообмена с окружающей средой.

9.1. Особенности теплообмена оребренных поверхностей

Рассмотрим процесс теплообмена оребрённых поверхностей радиаторов двух типов - и(рис.9.1.1.), при этом выясним, как изменяется рассеиваемая мощность в зависимости от числа ребер, их толщины, высотыи расстояния между ними при постоянной температуре радиатора и температуре среды.

Будем полагать, что ребра и оcнование радиатора ориентированы вертикально, вся тепловая энергия рассеивается конвенцией и излучением.

Поскольку конвективный и лучистый теплообмен различных поверхностей радиатора имеет свои особенности, разобьем всю его поверхность на nчастей_, , для радиатора типаи, и_, - для радиатора типа.

В пределах каждой -ой поверхности температура в любой точке будет различной. В первом приближении, не делая большой ошибки, примем, что температура поверхности радиатора во всех точках одинакова и равна.

Рис. 9.1.1. Конструкции радиаторов: а - плоский односторонне оребренный; б - радиально оребренный

Тогда мощность, рассеиваемая всей поверхностью радиатора в окружающую среду, температура которой , будет

,

где - мощность рассеиванияi-ой поверхностью, - температура среды, с которой -я поверхность находится в теплообмене,- площадь -ой поверхности.

Для поверхностей и = , для поверхностейи >за счет нагрева воздуха между ребрами.

Введем обозначение , откуда, в результате получим

, (9.1.1)

. (9.1.2)

Очевидно, коэффициент для поверхностей,ибудет равен единице, для поверхностейи- меньше единицы. Коэффициентучитывает уменьшение конвективного коэффициента теплоотдачи внутренних поверхностей ребер за счет повышения температуры воздуха между ребрами.

Коэффициент является функцией некоторого параметра, который в свою очередь, зависит от координат точки между ребрами, для которой определяется температура и критерий Грасгофа (рис. 9.1.2)

,.

При расчете координаты точки принимаем равными

,,.

Рис. 9.1.2. К выводу параметра

Подставив в выражения икоординаты точки, после преобразования получим

; (9.1.3)

где иизмеряются в мм,- параметр, характеризующий физические свойства среды при температуре.

Зависимость табулирована и дается в библиографическом списке [3].

Расстояние между ребрами для радиатора типаСпринимаетcя равным среднему значению

.

Конвективный и лучистый коэффициенты теплоотдачи в выражении (9.1.2) находится по известным формулам:

,.

Приведенная степень черноты для поверхностейиравна степени черноты радиатора, для поверхностейиопределяется по известной формуле

.

Коэффициент облученности - я поверхность - средадляравен единице. Для поверхностейион находится из отношения «натянутой» поверхности и внутренней поверхности между ребрами .

Для радиатора типа

, (9.1.4,а)

для радиатора типа

. (9.1.4,б)

Площади - ых поверхностей находятся из выражений:

Для радиатора типа Типа

;;

;;

;

.

Рассмотрим, как зависит мощность, рассеиваемая радиатором, от количества ребер при неизменной средне поверхностной температуре радиатора.

При увеличении числа ребер увеличивается теплоотдающая поверхность радиатора, что должно приводить при неизменной температуре к увеличению рассеиваемой мощности. Однако увеличение количества ребер при одних и тех же размерах основанияиприводит к уменьшению расстояния между ребрамии следовательно к уменьшению как конвективной составляющей коэффициента теплоотдачи вследствие повышения температуры между ребрами, так и лучистой составляющей вследствие уменьшения коэффициента облученности внутренней поверхности ребер - среда. Зависимостьпредставлена на рис. 9.1.3,а.

Рис. 9.1.3. Зависимости: а - , б -

Зависимость рассеиваемой радиатором мощности от числа ребер удобно представлять в виде функции

, (9.1.5)

где - коэффициент эффективности оребрения, равный отношению мощностей, рассеиваемых оребренной и неоребренной поверхности при одинаковых температура,- коэффициент оребрения, равный отношению площадей оребренной и неоребренной поверхностей.

Увеличение числа рёбер соответствует увеличению коэффициента оребрения и, следовательно, зависимость должна иметь экстремальное значение (рис. 9.1.3,б).

Найдём связь коэффициента оребрения с количеством ребери расстояния между ними.

Для радиатора типа имеем

,

откуда число ребер равно

(9.1.6,а)

Расстояние между ребрами найдём из выражения :

. (9.1.7)

Для радиатора типа

,

откуда (9.1.6,б)

и . (9.1.8)

Рассмотрим, как влияет на мощность, рассеиваемую радиатором, толщина, высота ребра и теплопроводность материала.

При постоянном количестве ребер увеличение их высоты приводит к увеличению теплоотдающей поверхности радиатора. При этом конвективный коэффициент теплоотдачи практически не изменяется, лучистый же коэффициент уменьшается вследствие уменьшения коэффициента облученности внутренние поверхности ребер – среда. В результате с увеличением высоты ребра рассеиваемая мощность увеличивается до некоторой максимальной величины, и с некоторой высотыуменьшается.

Уменьшение толщины ребра при постоянной его высоте приводит к увеличению неравномерности температурного поля по высоте ребра и эта неравномерность тем больше, чем меньше соотношениеи меньше теплопроводность материала.

Найдём соотношение между толщиной ребра и его высотой, при котором неравномерность температурного поля несущественно сказывается на эффективности радиатора.

Представим ребро как стержень, в основание которого втекает тепловой поток (рис. 9.1.4). Распределение температуры перегревапо высоте ребраописывается выражением

, (9.1.9)

где ,- периметр поперечного сечения ребра,- площадь поперечного сечения.

Перегрев у основания ребра при , как видно из (9.1.9), равен

. (9.1.10)

Рис. 9.1.4. К выводу отношения толщины к высоте ребра

Интегрируя (9.1.9) в пределах от дои деля результат на площадь ребра, получим средне поверхностный перегрев, относя который к перегреву ребра у основания, то есть при, получим

(9.1.11)

При неравномерность температурного поля составляет меньше 25 %, при этом

. (9.1.12)

Для сравнительно невысоких ребер (< 40…50 см) толщиной более 1,5…2 мм из хорошо проводящих материалов температурное поле их практически равномерно, т.е. температура у основания не намного отличается от средне поверхностной температуры.

Эффективность радиатора, то есть мощность, снимаемая с единицы оребренной поверхности, зависит и от профиля ребра. Наименьшей эффективностью обладает ребра прямоугольного сечения, наибольшей - ребра, представляющие в поперечном сечении параболу (рис. 9.1.5). Стремясь приблизиться к такой форме ребра, изготовляют трапециевидного или даже треугольного сечения.

Увеличение эффективности при этом объясняется увеличением коэффициента облученности внутренних поверхностей ребер - среда, а также увеличением среднего расстояния между ними, что приводит к увеличению коэффициента .

Рис. 9.1.5. Формы поперечного сечения ребер радиаторов

Помимо эффективности, как показывают расчеты, радиаторы, рассеивающие одинаковую мощность при прямоугольном сечении ребра, требуют на 50 %, треугольные на 4 % больше материала, чем радиаторы с параболическим сечением ребра.

Мощность, рассеиваемая радиатором с ребрами трапециевидного или треугольного сечения, рассчитывается по формуле

,

где - коэффициент теплоотдачи оребренной поверхности радиатора с прямоугольным ребром, длина, высота и толщина которого равны длине, высоте и средней толщине сужающегося ребра,- площадь оребренной поверхности радиатора с трапециевидными или прямоугольными ребрами;и- толщина ребра и температура, соответственно, у вершин и основания ребра,- поправочный коэффициент на суженность ребра

.

Отношение находится для эквивалентного прямоугольного ребра из выражения (9.1.9) прии. Это отношение после преобразований имеет вид

.

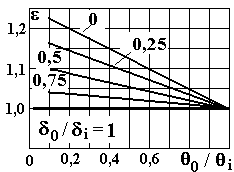
Рис. 9.1.6. График зависимости

Зависимость даётся в виде графиков (рис. 9.1.6).