2.3.2. Уравнение теплопроводности Фурье

Полученное ранее выражение теплового потока справедливо при стационарном одномерном температурном поле. В общем случае, как указывалось, температура в любой точке тела является функцией трех координат. Кроме того, она может меняться и во времени. Протекание теплового процесса в любой точке тела в любой момент времени описывается дифференциальным уравнением Фурье, которое является основным уравнением теплопроводности. Решение этого уравнения позволяет определить температуру в любой точке тела в любой момент времени.

Дифференциальное уравнение теплопроводности выводится на основе закона сохранения энергии. Для этого выделяют в исследуемом теле элементарный параллелепипед объемом dvс ребрамиdx, dy, dz(рис. 2.3.2). Считают, что в пределах выделенного объема тело однородно и изотропно (коэффициенты теплопроводности по координатным осям одинаковы). Кроме того, принимают, что коэффициенты теплопроводности не зависят от температуры.

Для общности рассуждения полагают, что тело имеет внутренние источники тепла, равномерно распределенные по объему. Количество тепла , введенное за времяdв элемент объема через его грани, и количество тепла , выделяемое за это же время внутренними источниками тепла, изменяют его внутреннюю энергию на величину

= + . (2.3.8)

Изменение внутренней тепловой энергии тела пропорционально его температуре

dQ = c  dv dt, (2.3.9)

где c_p- удельная теплоемкость,, - плотность, кг/м³.

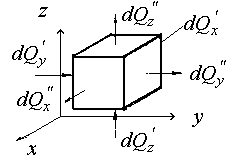
Рис. 2.3.2. К выводу дифференциального уравнения теплопроводности Фурье

Производится подсчет притока тепла через грани элемента за времяd (рис. 2.3.2.).

Количество тепла ,протекающего по направлению осиx через граньdy dz,равно = q_x dy dz d .

Количество тепла , утекающего из объема по направлению осиx,будет равно = q_x+dx dy dz d.

Приращение тепловой энергии в объеме за счет разности притока и стока энергии равно

= - = (q_x -q_x+dx) dy dz d.

Приращение dxмало, поэтому, следовательно.

Плотность теплового потока, согласно закону Фурье, равна

.

Подставляя значение q_xв предыдущее выражение, получают

.

Аналогично рассуждая, выражения для по другим координатным осям можно записать

,.

Полное же количество тепла, переданное в объем через грани, равно

.

Количество тепла dQ₂, выделяемое в объемеdvвнутренними источниками тепла, равно, гдеW– удельная мощность источников тепла, Вт/м³.

Суммарное приращение количества тепла в объеме dvза времяdв соответствии с (2.3.8) записывается в виде

. (2.3.10)

Приравнивая правые части выражений (2.3.9) и (2.3.10), получают

,

или , (2.3.11)

где -коэффициент температуропроводности, характеризующий скорость изменения температуры в теле.

Выражение (2.3.11) называют уравнением теплопроводности Фурье.

Для стационарного температурного поля (dt/d = 0) выражение (2.3.11) принимает вид

. (2.3.11,а)

Для анизотропных тел, у которых коэффициенты теплопроводности λ_x, λ_y, λ_zразличны по координатным осям, уравнение Фурье имеет вид

. (2.3.11,б)

Это уравнение путем преобразования системы координат в виде

приводится к уравнению, аналогичному для изотропного тела (2.3.11), где вместо x, y, zподставляются преобразованные координатыx’, y’, z’.

При преобразовании координат λесть некоторая базовая теплопроводность, выбор которой произволен. Обычно принимается заλ одно из значений коэффициента теплопроводности , .

Для решения дифференциального уравнения необходимо иметь начальные и граничные условия, соответственно характеризующие начальное распределение температуры в теле, и особенности протекания процесса теплообмена с поверхности тела в окружающую среду.