3. Гауссовский случайный процесс
Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом. Одномерная плотность вероятности нормального процесса определяется выражением:
(2.89)
В данном случае будет рассматриваться стационарный и эргодический гауссовский процесс. Поэтому подmxиxможно подразумевать соответственно постоянную составляющую и среднюю мощность флуктуационной составляющей одной (достаточно длинной) реализации случайного процесса.
Графики плотности вероятности при нормальном законе для некоторых значений xизображены на рис. 2.24. Функцияp(x)симметрична относительно среднего значения. Чем большеx, тем меньше максимум, а кривая становится более пологой [площадь под кривойp(x)равна единице при любых значенияхx].
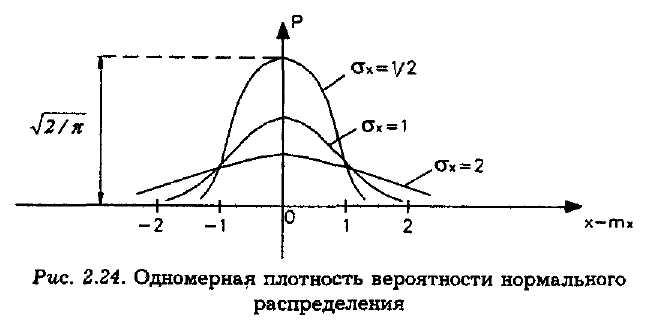
Рис. 2.24. Одномерная плотность вероятности нормального распределения
Широкое распространение нормального закона распределения в природе объясняется тем, что при суммировании достаточно большого числа независимых или слабо зависимых случайных величин распределение суммы близко к нормальному при любом распределении отдельных слагаемых.
Это положение, сформулированное в 1901 г. А.М. Ляпуновым, получило название центральной предельной теоремы.
Наглядными физическими примерами случайного процесса с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Не только шумы и помехи, но и полезные сигналы, являющиеся суммой большого числа независимых случайных элементарных сигналов, например, гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гауссовские случайные процессы.
На основе функции p(x)можно найти относительное время пребывания сигналаx(t)в определенном интервале уровней, отношение максимальных значений к среднеквадратическому (пик фактора) и ряд других важных для практики параметров случайного сигнала.
Отношение времени пребывания x(t)в заданном интервале к общему времени наблюдения можно трактовать как вероятность попаданияx(t)в указанный интервал. При этом следует заметить, что данные о распределении вероятностей не дают никаких представлений о поведении функцииx(t)во времени.
4. Спектральная плотность мощности случайного процесса
Подразумевая под случайным процессом множество (ансамбль) функций времени, необходимо иметь в виду, что функциям, имеющим различную форму, соответствуют различные спектральные характеристики. Усреднение комплексной спектральной плотности, введенной в п. 2.5, по всем функциям приводит к нулевому спектру процесса (при M[x(t)]=0из-за случайности и независимости фаз спектральных составляющих в различных реализациях. Можно, однако, ввести понятиеспектральной плотности среднего квадрата случайной функции, поскольку значение среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случайной функциейx(t)подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощность, выделяемую сопротивлением 1 Ом. Эта мощность распределена по частотам в некоторой полосе, зависящей от механизма образования случайного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1 Гц при заданной частоте. Размерность функцииW(), являющейся отношением мощности к полосе частот, есть:
Спектральную плотность случайного процесса можно найти, если известен механизм образования случайного процесса. Здесь мы приведем только определение общего характера.
Выделив из ансамбля какую-нибудь реализацию xk(t)и ограничив ее длительность конечным интерваломT, можно применить к ней обычное
.
преобразование Фурье и найти спектральную плотность XKT(). Тогда энергию рассматриваемого отрезка реализации можно вычислить с помощью формулы (2.73):
(2.90)
Разделив эту энергию на T, получим среднюю мощностьk-й реализации на отрезкеT:
(2.91)
При увеличении TэнергияEвозрастает, однако отношениеE/Tстремится к некоторому пределу. Совершив предельный переходT∞, получим:
где
(2.92)
представляет собой спектральную плотность средней мощности k-й реализации.
В общем случае величина Wk()должна быть усреднена по множеству реализаций. Ограничиваясь в данном случае рассмотрением стационарного и эргодического процесса, можно считать, что найденная усредненная по одной реализации функцияWk()характеризует весь процесс в целом. Опуская индексk, получаем окончательное выражение для средней мощности случайного процесса:
где
(2.93)
Энергетический спектр, естественно, не несет в себе сведений о фазовых соотношениях. Восстановить реализации процесса как функции времени по энергетическому спектру нельзя.