2.10. Случайные сигналы и их аналитическое описание

В реальных условиях при передаче информации сигнал в месте приема заранее неизвестен и потому не может быть описан определенной функцией времени. То же самое можно сказать и о помехах, появление которых обусловлено самыми различными и чаще всего неизвестными причинами.

Таким образом, реальные сигналы и помехи представляют собой случайные процессы. Случайный процесс описывается случайной функцией, значения которой при любом значении аргумента являются случайными величинами. В отличие от детерминированной функции, однозначно определяющей и, таким образом, достоверно предсказывающей значение описываемой величины в любой заданный момент времени, ход случайной функции предсказан быть не может. Самое большое, что можно сказать заранее о поведении случайной функции – это вероятность, с которой она в будущем может принять тот или иной вид из множества возможных.

В ряде практически важных задач случайный процесс наряду с вероятностным описанием можно описать совокупностью неслучайных числовых характеристик, постоянных или меняющихся во времени. От этих характеристик требуется, чтобы в условиях конкретно поставленной задачи они отражали самое существенное случайного процесса.

1. Одномерный закон распределения мгновенных значений случайной функции и связанные с ним основные характеристики

Случайный процесс обозначим случайной функцией X(t), значения которой в любой заданный момент времени не могут быть точно предсказаны, т.е. являются случайными величинами. Определенный вид x(t), принятый случайной функцией X(t) в результате опыта, называют реализацией случайной функции или процесса (рис. 2.21).

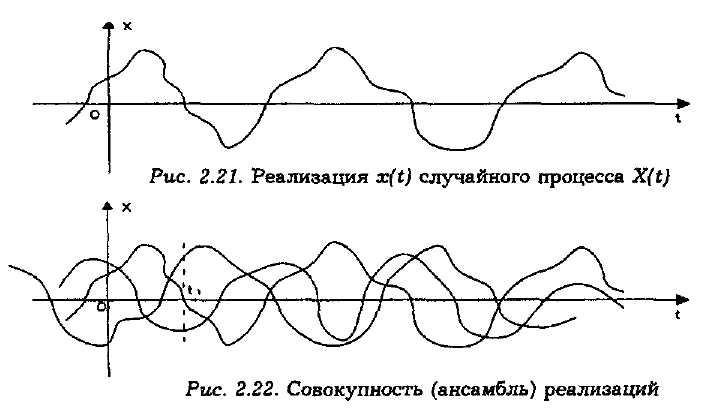
Рис. 2.21. Реализация x(t) случайного процессаX(t)

Рис. 2.21. Совокупность (ансамбль) реализаций

Под опытом или испытанием понимается, например, однократное включение источника случайного процесса на некоторое время с соответствующей записью колебания. В результате многократного повторения опыта с данным источником можно получить множество реализаций процесса, внешне совершенно не похожих одна на другую. Для получения реализаций процесса таким путем необходима повторяемость условий испытаний. Во многих случаях повторяемость условий испытаний единственного источника не может быть соблюдена, так как параметры источника необратимо меняются во времени. В этих условиях следует оперировать понятием не единственного источника, а их множества. В результате опыта, предусматривающего параллельную работу источников, получаем множество реализаций. При этом источники могут быть неидентичными, их параметры имеют разброс и меняются во времени.

Случайный процесс полностью характеризуется бесконечным множеством реализаций, образующих ансамбль. Понятием ансамбля, состоящего из бесконечно большого числа реализаций (рис. 2.22), удобно пользоваться при установлении статистических закономерностей, свойственных случайным процессам. Совокупность мгновенных значений случайного процесса, заданного ансамблем, в произвольный момент времени называют сечением случайного процесса.

Если зафиксировать произвольный момент времени t₁ (рис. 2.22), т.е. получить сечение случайного процесса, то для этого сечения может быть вычислено распределение вероятности P(x) непрерывной случайной величины X(t₁):

(2.77)

n – общее число значений величины X(t₁), удовлетворяющих условию:

X(t₁)X, (2.78)

N – общее число реализаций x(t).

Отношение n/N в теории вероятностей называют частотой наступления события. В данном случае под событием следует понимать выполнение условия (2.78). Приближенно при достаточно большом N можно считать:

Плотность вероятности случайной величины X(t₁) по определению в теории вероятностей выражается так:

(2.79)

и является производной по x функции (2.77). Выражения (2.77) или (2.79) статистически полностью характеризуют значения случайной функции X(t) в заданный момент времени t₁ и выражают ее одномерный закон распределения. Если момент t₁ выбирать произвольно, то в соответствии с (2.77) и (2.79) можно получить одномерный закон распределения в виде зависимости от времени P(x, t) или p(x, t).

Если закон распределения зависит от рассматриваемого момента времени t, то говорят о нестационарности случайного процесса, о неоднородности его протекания во времени. Необходимым условием стационарности процесса является независимость одномерного закона распределения от времени, т.е. выполнение одного из равенств:

P(x, t) = P(x), p(x, t) = p(x).

Одномерные законы распределения (2.77) или (2.79) удовлетворяют условию:

∞

P(∞) =  p(x)dx = 1,

-∞

отражающему достоверность того, что величина X(t₁) обязательно примет одно из значений, находящихся в пределах от -∞ до +∞.

Наряду с вероятностными характеристиками P(x) случайной величины могут рассматриваться ее числовые характеристики, или моменты случайной величины.

Среднее значение случайной величины X(t₁), или момент первого порядка

____

m_x = X(t₁) = M₁[X(t₁)]

называют математическим ожиданием случайной величины. Прямая черта над X(t₁) в данном случае означает операцию усреднения случайной величины X(t₁) по ансамблю реализаций. По определению момент первого порядка выражается следующим образом:

∞

m_x = M₁[X(t₁)] =  xp(x, t₁)dx. (2.80)

-∞

Среднее значение квадрата случайной величины, или момент второго порядка:

_____

X²(t₁) = M₂[X(t₁)]

представляет в широком смысле мощность случайного процесса, которая выделяется на единичной нагрузке и характеризует его интенсивность. По определению момент второго порядка выражают формулой математического ожидания квадрата случайной величины:

∞

M₂[X(t₁)] =  x²p(x, t₁)dx. (2.81)

-∞

Вычитая из случайной величины X(t₁) ее среднее значение, получим новую, так называемую центрированную случайную величину:

____

X⁰(t₁) = X(t₁) – X(t₁).

Очевидно, что:

____

M[X(t₁) – X(t₁)] = 0.

Среднее значение квадрата центрированной случайной величины называют дисперсией:

M₂[X⁰(t₁)]= ²[X(t₁)]. (2.82)

Она характеризует мощность отклонений случайной величины от ее среднего значения, выделяемую на единичной нагрузке. Нетрудно установить, что:

∞

²(t₁) = M₂[X⁰(t₁)] =  x²p(x⁰, t₁)dx, (2.83)

-∞

где p(x⁰, t₁) – плотность вероятности случайной величины.

Дисперсия является мерой разброса значений случайной функции около среднего значения, поэтому величину (t) еще называют средним квадратическим уклонением.

____

Заметим, что X(t₁) отличается от X⁰(t₁) на неслучайную величину X(t₁). Поэтому законы распределения p(x, t₁) и p(x⁰, t₁) отличаются лишь смещением по x:

____

p(x⁰, t₁) = p[x – X(t₁), t₁].

Так как t₁ – произвольный момент времени, числовые характеристики можно понимать как функции времени:

M₁[X] = M₁[t]; M₂[X] = M₂[t]; M₂[X⁰] = ²(t).

Для стационарного процесса величины M₁[X], M₂[X], ² от времени не зависят.