ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Московский государственный институт радиотехники, электроники и автоматики

(Технический Университет)

МИРЭА

ТЕОРИЯ ПЕРЕДАЧИ ИНФОРМАЦИИ

Методические указания по выполнению практических занятий и самостоятельной работы

Для студентов специальности 220201

Москва 2007

Составитель Я.М. Ковальчук

Методические указания содержат варианты индивидуальных заданий и рекомендации по выполнению практических занятий и самостоятельной работы по курсу «Теория передачи информации».

Материал предназначен для студентов дневного отделения, изучающих курс «Теория передачи информации».

Московский государственный

институт радиотехники, электроники и

автоматики (Технический Университет),

2007

Преобразования сообщений в системах передачи информации.

В работе рассматриваются преобразования сообщений в указанном порядке: аналоговые непрерывные сообщения – квантизация сообщений – первичное кодирование – помехоустойчивое кодирование – модуляция – демодуляция – декодирование (получение дискретной функции) – восстановление (сглаживание) непрерывных функций.

Исходные данные даны в табл.1.

1. Номер варианта от 0 до 23 определяется путем деления шифра на 25 и соответствует остатку (графа 2 задания).

2. По номеру варианта выбрать аналоговое непрерывное сообщение – непрерывную функцию по рис.1 – рис.6 (графа3).

3. В соответствии с указанным типом квантизации (графа 4 задания) осуществить квантование и дискретизацию (дискретизацию и квантование) выбранной непрерывной функции. Шаг квантования и граничная частота, F_c, для определения шага равномерной дискретизации указаны в табл.2. Характеристика нелинейного квантователя, элемента (НЭ) – указана в задании (графа 5).

4. Выполнить кодирование дискретных величин, полученных в результате квантизации первичным (некорректирующим) двоичным кодом.

5. Произвести кодопреобразование первичного кода (некорректирующего) в корректирующий код. Тип кода задан в графе 6 задания.

6. В соответствии с графами 7 и 8 задания выбрать переносчик и осуществить модуляцию.

7. Используя значения вероятности искажения двоичных символов р (графа 9 задания), рассчитать вероятность безошибочно приема Р_бо, вероятность ошибки Р_ош, вероятность обнаруживаемой ошибки Р_оо, вероятность необнаруживаемой ошибки Р_но.

8. Провести демодуляцию и декодирование и получить сообщение в виде дискретной функции.

9. По заданному типу аппроксимации (графа 10 задания) восстановить непрерывную функцию.

10. В работе приводятся определения всех процессов и их описание, приводятся характеристики процессов.

11. Результат выдается в виде текста, графиков, таблиц и др.

Таблица 1

Исходные данные для выполнения курсовых работ

по преобразованию сообщений

№ п/п	№ вар	№ функ-ции	Способ кванти- зации	Характе- ристики квантова -теля НЭ	Тип корректи- рующего кода	Тип им-пульсного перенос-чика	Модули-руемый параметр	Вероятность искажения двоичных символов	Тип апрокси-мации
1	2	3	4	5	6	7	8	9	10
1 2 3 4	0 1 2 3	1.1 1.2 1.3 1.4	кв.-диск. диск.-кв. кв.-диск. диск.-кв.	а б г а	пров. на чет. пов. без инв. кор. код пов. с инв.	видео видео видео видео	ам пол tим ам	2·10-4 4·10-5 4·10-5 5·10-5	лин.инт. ст. апр. ст. апр. ст. апр.
5 6 7 8	4 5 6 7	2.1 2.2 2.3 2.4	кв.-диск. диск.-кв. кв.-диск. диск.-кв.	б г д а	пов. без инв. пров. на чет. пост. вес кор. код	радио радио радио радио	ам fи φи tим	3·10-4 6·10-5 3·10-4 6·10-5	ст. апр. лин.инт. лин.инт. лин.инт.
9 10 11 12	8 9 10 11	3.1 3.2 3.3 3.4	кв.-диск. диск.-кв. кв.-диск. диск.-кв.	б г д г	пов. без инв. пов. с инв. пров. на чет. пост. вес	радио радио радио радио	fи φи tим ам	4·10-5 8·10-5 6·10-5 5·10-5	ст. апр. ст. апр. лин.инт. лин.инт.
13 14 15 16	12 13 14 15	4.1 4.2 4.3 4.4	кв.-диск. диск.-кв. кв.-диск. диск.-кв.	д а б г	кор. код пров. на чет. пов. с инв. пов. без инв.	видео видео видео видео	пол tим ам пол	4·10-4 8·10-5 4·10-4 6·10-5	ст. апр. лин.инт. лин.инт. лин.инт.
17 18 19 20	16 17 18 19	5.1 5.2 5.3 5.4	кв.-диск. диск.-кв. кв.-диск. диск.-кв.	д а б г	пост. вес пров. на чет. кор. код кор. код	видео видео видео видео	tим ам пол tим	8·10-5 8·10-5 6·10-5 8·10-5	лин.инт. ст. апр. ст. апр. ст. апр.
21 22 23 24	20 21 22 23	6.1 6.2 6.3 6.4	кв.-диск. диск.-кв кв.-диск. диск.-кв.	а б г б	пост. вес пов. с инв. пов. без инв. пост. вес	радио радио радио радио	fи φи tим ам	6·10-5 8·10-5 2·10-4 2·10-4	ст. апр. лин.инт. лин.инт. лин.инт.

Пояснения к исходным данным, представленным в таблице 1.:

гр. 4 – способ квантизации: кв.-диск. – квантование, потом дискретизация, диск.-кв. – дискретизация, потом квантование.

гр. 5 – характеристики квантователя (нелинейного элемента): приведены на рис.9 и рис.11.

гр. 6 – тип корректирующего кода: пров. на чет. – проверка на четность, пов. без инв. – повторение без инверсии, кор. код. – корреляционный код, пов. с инв. – повторение с инверсией, пост. вес – код с постоянным числом единиц (постоянным весом).

гр. 7 – тип импульсного переносчика: видео – последовательноть видеоимпульсов, радио – последовательность радиоимпульсов.

гр. 8 – модулируемый параметр: ам – амплитуда, пол – полярность, t_им– длительность импульса, f_и– частота колебаний в импульсе,φ_и– фаза колебаний в импульсе.

гр. 10 – Тип аппроксимации: ст. апр. – ступенчатая аппроксимация, лин.инт. – линейная интерполяция.

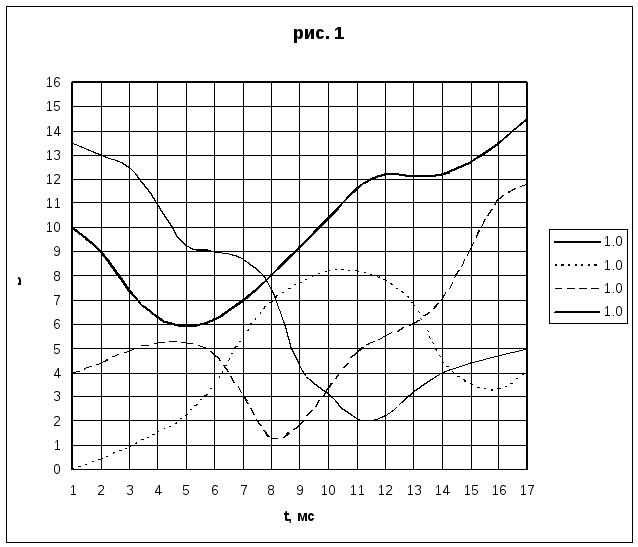
Таблица 2.

Рис., ряд	2-1	2-2	2-3	2-4	3-1	3-2	3-3	3-4	4-1	4-2	4-3	4-4
Fc, кГц	0,5	0,6	0,6	0,5	0,5	0,5	0,6	0,6	0,5	0,6	0,5	0,6
∆y, В	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0

Рис., ряд	5-1	5-2	5-3	5-4	6-1	6-2	6-3	6-4	7-1	7-2	7-3	7-4
Fc, кГц	0,5	0,5	0,6	0,6	0,5	0,5	0,6	0,6	0,5	0,5	0,6	0,6
∆y, В	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0	1,0

В методических указаниях рассматриваются следующие преобразования:

1. Дискретизация и квантование – преобразование непрерывного сообщения в дискретное.

2 Первичное кодирование сообщений – преобразование дискретных аналоговых величин в кодовые комбинации.

3 Помехоустойчивое кодирование – преобразование первичных кодов в корректирующие.

4. Модуляция сообщений – преобразование кодовых комбинаций корректирующего кода в сигнал

5.Демодуляция сигналов – преобразование сигналов в кодовые комбинации.

6.Декодирование – преобразование принятых кодовых комбинаций в первичный код, а затем в дискретную аналоговую величину.

7 Получение непрерывных сообщений по дискретам – аппроксимация или интерполяция дискретных функций

8. Рассматривается также помехоустойчивость корректирующих кодов: вероятность появления ошибок различной кратности, вероятность не обнаружения ошибки, другие вероятности.

Теоретические предпосылки и методические указания по выполнению работы

Рассмотрим эти виды преобразований более подробно.

1 Дискретизация и квантование непрерывных сообщений.

Сведения, подлежащие передаче от отправителя к получателю, называются сообщениями. Сообщения могут существовать либо в знаковой, либо в аналоговой форме. Сообщение в знаковой форме всегда дискретны, так как состоят из отдельных знаков.

Сообщения же в аналоговой форме могут иметь различный по своему характеру вид. Естественно выделить четыре основных вида таких сообщений.

1. Непрерывные сообщения: их математическое описание имеет вид функции y=f(x), непрерывной как по аргументу х, так и по значениям функции у (рис.7,а)

2. Непрерывно – дискретные: их математическое описание имеет вид ступенчатой функции y_j =(x). В диапазоне значений [y_min,y_max] такая функция принимает конечное число значений (рис. 7,б).

3. Дискретно-непрерывные: функция y=(x_i) дискретна по аргументу, но непрерывна по значениям у. В интервале значений аргумента [x_min,x_max] функция имеет конечное число значений, отличных от нуля, из бесконечного множества значений в диапазоне [y_min,y_max] (рис. 7,в). Такая функция называется решетчатой.

4. Дискретные (аналоговые): функция y_j =(x_i) дискретна и по аргументу, и по значениям (рис. 7,г).

Рис. 7

Физический процесс непрерывен по аргументу (время, пространственная координата), поэтому аналоговые сообщения, полученные от источника и подлежащие передаче, имеют не прерывный вид (рис. 7 а). Передача же сообщений осуществляется, в основном, цифровыми способами (цифровые системы передачи информации), потому исходное сообщение необходимо представлять в дискретном виде (рис.7 г). Как видно из рисунка, сообщение представлено дискретными величинами в моменты времени t_i.

Переход от не прерывного вида к дискретному осуществляется с помощью операции квантизации - совместного поочередного квантования и дискретизации или дискретизации и квантования. Очередность квантизации для каждого из вариантов дана в графе 4 таблицы.