Линейный не систематичекий код

(КОД ХЭМММИНГА НЕ СИСТЕМАТИЧЕСКИЙ)

Этот код является разделимым не систематическим линейным кодом длины n с k информационными и r проверочными символами, обозначается как (n,k)-код. (7,4)- код Хэммминга позволяет обнаруживать одиночные и двойные ошибки и ряд ошибок большей кратности или исправлять одиночную ошибку.

Построение корректирующего кода.

В качестве первичного (исходного) берется двоичный код на все сочетания с числом информационных символов k, к которому добавляется проверочные символы r , общая длина комбинации кода n = k + r.

Определение числа контрольных символов.

Для этого можно воспользоваться следующими рассуждениями. При передаче по каналу с шумами может быть или искажен любой из n символов кода, или слово передано без искажений. Таким образом, может быть n+1 вариант искажения (включая передачу без искажений). Используя контрольные символы, необходимо различить все n+1 вариантов. С помощью контрольных символов r можно описать 2^r событий. Значит, должно быть выполнено условие: 2^r ≥ n +1 = k + r +1

В таблице представлена зависимость между n, k и r полученная из этого неравенства.

Таблица 2

Число проверочных символов r в коде Хэмминга

в зависимости от числа информационных символов k

2r	4	8	8	8	16	16	16	16	16	16	6	32	32
k+r+1	4	6	7	8	10	11	12	13	14	15	16	18	19
k	1	2	3	4	5	6	7	8	9	10	11	12	13
r	2	3	3	3	4	4	4	4	4	4	4	5	5

Размещение проверочных символов. В принципе место расположения проверочных символов может быть произвольным. Однако, произвольное расположение проверочных символов затрудняет проверку принятого кода. Для удобства обнаружения искаженного символа и его исправления целесообразно размещать их на местах, определяемых по значению 2ⁱ (i = 0 ÷ n–1), т.е. на позициях 1,2,4,8, и т.д. Информационные символы располагаются на оставшихся местах. Поэтому, например, для семиэлементной закодированной комбинации можно записать b₁b₂a₁b₃a₂a₃a₄.

Значения информационных символов a₁a₂a₃a₄ определяется первичным двоичным кодом на все сочетания. Первичный код имеет 2^k=N комбинаций.

Значения проверочных символов в коде определяются из выражения:

b₁=a₁a₂a₄, b₂=a₁a₃a₄, b₃=a₂a₃a₄

Пример построения комбинации корректирующего кода. Пусть комбинация первичного кода будет 1001 тогда:

a₁=1, a₂ =0, a₃=0, a₄=1.

Значения проверочных символов:

b₁=a₁a₂a₄= 101=0 b₂=a₁a₃a₄ =101=0 b₃=a₂a₃a₄=001=1

Комбинация корректирующего кода будет иметь вид:

b₁ b₂a₁ b₃a₂a₃a₄=001001

Характеристики не систематического (n,k)-кода на примере (7,4)-кода.

1. Код разделимый, длины кода – n

2. Число информационных символов k, число поверочных символов r = n – k

3. Кодовое расстояние d, равно минимальному весу его ненулевых комбинаций

4. Избыточность кода И =(n – k) / k

5. Корректирующая способность кода. Код обнаруживает все однократные и двухкратные ошибки и некоторые ошибки большей кратности. Код исправляет однократные ошибки.

Обнаружение ошибок. Обнаружение ошибки сводится к проверке выполнения соотношений и нахождению синдрома ошибки для каждой принимаемой комбинации:

При исправлении ошибки по тем же правилам находится синдром. Синдром представляет собой r - разрядное двоичное число, указывающее позицию искаженного символа S=S₃ S ₂S₁,

Пример: передаваемая комбинация =0011001. Искажен четвертый символ, тогда принятая комбинация:

0010001=b₁^*b₂^*a₁^* b₃^*a₂^*a₃^*a₄^*

Синдром определяется в соответствии с формулами: S₁=a₁^*a₂^*a₄^*b₁^*=1010=0, S₂=a₁^*a₃^*a₄^*b₂^*=1010=0, S₃=a₂^*a₃^*a₄^*b₃^*=0010=1 S=S₃ S ₂S₁=100.

Двоичное число 100 указывает на искажение 4-го символа. После замены значения четвертого символа на инверсный получается исходная комбинация 0011001. В приведенной ниже таблице указан синдром и соответствующий ему искаженный символ, который обнаруживается и исправляется.

Таблица 3

Комбинация корректирующего кода b1 b2 a1 b3 a2 a3 a4	Вектор ошибки еi	Искаженная комбинация, позиции символа b1*b2*a1*b3*a2*a3*a4* 1 2 3 4 5 6 7	S	Номер позиции искаженного символа
0010001	0000001
	0000010
	0000100
0011001	0001000	0011001	100	четвертый
	0010000
	0100000
	1000000
	0000000

Вероятность передачи определяется как вероятность обнаружения ошибки при использовании (n,k)-кода в качестве обнаруживаемого ошибку или как вероятность исправления одиночной ошибки при использовании (n,k)-кода в качестве исправляющего одиночную ошибку.

ЦИКЛИЧЕСКИЕ КОДЫ – КОД НА ОСНОВЕ ТЕОРИИ МНОГОЧЛЕНОВ.

Многие линейные коды обладают следующим интересным свойством: если взять любую кодовую комбинацию V= (a₁a₂ .....a_kb₁ .....b_r) и осуществить циклический сдвиг всех ее элементов на один символ влево, то полученная в результате комбинация V⁽¹⁾= (a₂a₃ .....a_kb₁b₂.....b_ra₁) , будет также принадлежать этому коду. Линейные (n,k)-коды, обладающие указанным свойством, называются циклическими, а коды, не обладающие таким свойством, - нециклическими. Рассмотренный ранее (7,4)-код – код Хэммминга - является циклическим, в чем легко убедиться.

Для описания циклических кодов может быть применен тот же аппарат, что и для описания линейных кодов, поскольку всякий циклический код является линейным. Но ни теория матриц, ни теория линейных зависимостей не дают возможности наглядно отразить основное свойство таких кодов – цикличность комбинаций. Гораздо удобнее при изучении циклических кодов применять теорию многочленов. При этом полезно использовать возможность представления комбинаций эти кодов при помощи многочленов. Такое представление применимо к любым систематическим линейным (n,k)-кодам. Комбинацию линейного кода можно представить в виде: (a_n-1a_n-2 …a₁a₀). Такая комбинация отображается многочленом одной переменной с постоянными коэффициентами:

f(x)=a_n-1 x ^n-1+a_n-2 x ^n-2 + …. a₁ x + a₀ (26)

где коэффициенты a_n-1a_n-2 …a₁a₀ принимают одно из двух значений: 0 или 1.

Например, комбинации 1100101 соответствует многочлен:

f(x)= x ⁶+ x ⁵+ x ²+1. (27)

Ясно, что степень представляющего многочлена f(x) не может превышать n – 1, где n – длина кодовой комбинации.

Многочлен (25) умножается на x с учетом того, что степень f(x) в данном случае не может быть выше 6, x ⁷ заменяется на 1. Результат умножения будет иметь вид x ·f(x)= x ⁶+ x ³+ x +1.

Полученному многочлену соответствует кодовая комбинация 1001011. Нетрудно заметить, что она представляет собой результат циклического сдвига влево на один символ исходной комбинации.

Итак, циклический сдвиг кодовой комбинации линейного кода на один символ влево соответствует умножению представляющего ее многочлена f(x) на x с заменой x ⁿ на 1. Далее, если сложить по mod2 две комбинации линейного кода, то на языке многочленов это означает, что надо сложить два представляющих эти комбинации многочлена, причем коэффициенты при одинаковых степенях многочленов надо складывать по mod2. Например:

Рассмотрим возможности теории многочленов для изучения циклических кодов.

Анализируя циклический (n,k)-код следует найти такую комбинацию в которой код будет представлен многочленом с наименьшей возможной степенью. При изучении линейных кодов очевидно, что комбинация линейного кода может быть отличной от нуля только тогда, когда в ней хотя бы один информационный символ отличен от нуля. При этом наименьшей степенью обладает тот многочлен, который соответствует комбинации с единицей в младшем (самом правом) информационном разряде:

Полученный многочлен g(x) будет иметь степень r

g(x) = 00…01b₁b₂…b_r

Можно показать, что многочлен g(x) должен удовлетворять следующему условию: быть делителем двучлена xⁿ+1. Иными словами, комбинации линейного кода обладают свойством цикличности только тогда, когда многочлен g(x) является делителем двучлена xⁿ+1.

В рамках теории многочленов циклическим называют такой систематический линейных (n,k)-код, все 2^k комбинаций которого обладают следующим свойством: соответствующие им многочлены степени n–1 и менее делятся на некоторый многочлен g(x) степени r = n – k, являющийся делителем двучлена x ⁿ+1.

Многочлен g(x) называется порождающим или образующим многочленом циклического кода. Это обусловлено тем, что, зная этот многочлен, можно построить все комбинации соответствующего циклического кода. При этом свойства и возможности получаемого циклического кода полностью определяются степенью r и структурой порождающего многочлена.

Многочлен степени m называется неприводимым, если он не делится ни на какой другой многочлен положительной степени меньшей m.

Оказывается, каждый двучлен xⁿ+1 (практически для любого n) может быть представлен произведением нескольких неприводимых многочленов. Например:

x ⁷+1 = (x +1)( x ³+ x +1)( x ³+ x ²+1).

В этом легко убедиться, раскрыв скобки и сложив по mod2 коэффициенты при одинаковых степенях x.

Ясно, что каждый из этих неприводимых многочленов является делителем двучлена x⁷+1 (а в общем случае - двучлена xⁿ+1). Удовлетворяет и любое произведение отдельных сомножителей. Поэтому в качестве g(x) можно взять и любое такое произведение.

Все возможные порождающие многочлены, которые могут быть получены на основе двучлена x ⁷+1, сведены в таблицу 4.

Таблица 4

№	Делители двучлена (порождающие многочлены)	r	Код
1 2 3 4 5 6	g1(x) = x+1 g2(x) = x3 + x + 1 g 3(x) = x3 + x2 + 1 g4(x) = (x+1) (x3 + x + 1) = x4 +x3 + x2 + 1 g5(x) = (x+1) (x3 + x2 + 1) = x4 + x2 + x + 1 g6(x) = (x3 + x + 1) (x3 + x2 + 1) = x6 + x5 + x4 + x3 + + x2 +x + 1	1 3 3 4 4 6	(7,6) (7,4) (7,4) (7,3) (7,3) (7,1)

Зная порождающий многочлен g(x), легко найти порождающую матрицу циклического кода. В качестве строк этой матрицы обычно берется k линейно независимых комбинаций, соответствующих многочленам g(x), xg(x), x²g(x), ….., x^k-1g(x):

Остальные ненулевые комбинации циклического кода получаются, сложением по mod2 строк матрицы попарно, по три и т.д. – до сложения всех k строк.

Пример3: Построить порождающую матрицу циклического (7,4)-кода, задаваемого порождающим многочленом g(x) = x³ + x + 1:

Далее рассматривается вопрос обнаружения ошибок в комбинациях циклических кодов.

Проверочным многочленом циклического кода называется многочлен h(x) степени k, представляющий собой частное от делении двучлена xⁿ+1, на порождающий многочлен g(x):

(29)

Этот многочлен имеет вид:

h(x) = h_kx^k + h_k-1x^k-1 +…+ h₁ x+h₀ (30)

где h_k= h₀=1, а h_k-1,… h₁ , – либо 0, либо 1.

Проверочный многочлен h(x) обладает очень интересным свойством: он ортогонален любому многочлену V(x), соответствующему комбинации циклического кода, т.е.

V(x)·h(x)=0 (31)

На основании проверочного многочлена можно построить проверочную матрицу h_ц циклического кода. Для этого в качестве первой строки матицы следует брать комбинацию, соответсвующую многочлену , отличающемуся от проверочного многочленаh(x) лишь обратным порядком расположения степеней:

Остальные строки проверочной матрицы получают циклическим сдвигом первой строки на один символ вправо (т.к. степени распложены в обратном порядке, то домножение на x соответствует сдвигу всех символов не влево, а вправо). При этом проверочная матрица имеет вид:

(32)

Основное свойство этой матрицы заключается в следующем: для любой комбинации V циклического кода, порождаемого многочленом g(x), справедливо равенство

V·H^Т_ц = 0 (33)

(в правой части не один символ, а последовательность из r нулевых символов).

Выполнение этого равенства для какой-либо комбинации длиной n свидетельствует о ее принадлежности к циклическому коду. Этим и объясняется название «проверочный» для многочлена h(x) и самой матрицы H_ц.

Пример. Построить проверочную матрицу H_ц циклического (7,4)-кода с порождающим многочленом g(x) = x³ + x + 1.

Проверочный многочлен кода находится:

Многочлены, представляющие строки проверочной матрицы и сама матрица H_ц будут иметь вид:

=

Идея обнаружения ошибок в комбинациях циклических кодов та же, что и в случае линейных кодов: находится (вычисляется) синдром S и по его виду принимается решение, есть ошибка или нет. Отличие синдрома от нулевого, говорит о наличии ошибок. Синдром можно находить несколькими способами:

1. Как в линейных кодах (с применением теории линейных зависимостей или теории матриц).

2. Применяя свойство поражающего многочлена циклического кода g(x) быть делителем представляющего многочлена V_i(x). Оказывается, синдром можно получить как остаток от деления многочлена V_i^*(x), соответствующего принятой комбинации V_i^*, на порождающий многочлен g(x). Точнее, коэффициенты этого остатка и представляют собой комбинацию синдрома принятой комбинации. Мы примем это без доказательства. Способ нахождения синдрома делением V_i^*(x) на g(x) получил преимущественное распространение при обнаружении ошибок в комбинациях циклического кода благодаря простоте его технической реализации.

Пример. Найдем синдром комбинации V_i^*=(1111001), полученной из комбинации V_i=(1101001) (7,4)-циклического кода, порождаемого многочленом g(x) = x³ + x² + 1. Найдем остаток от деления многочлена, представляющего рассматриваемую комбинацию V_i^*, на порождающий многочлен:

Коэффициенты этого остатка дают комбинацию синдрома S=110. Ясно, что на посланную комбинацию подействовал вектор ошибок вида e =(0010000). Известно, что V_i^* = V_i  e_i.

Так как V_i – правильная комбинация, то в силу принадлежности циклическому коду она делится на g(x) без остатка.

Рассмотрим еще один способ построения циклического кода, основанный на использовании теории многочленов. Любой многочлен V_i(x) можно представить в виде суммы двух многочленов:

V_i(x) = A(x) + R(x), (34)

где A(x) – многочлен, представляющий информационные символы комбинации, R(x), – многочлен, представляющий проверочные символы. Например, для V_i =(1101001)многочлены будут иметь вид:

Многочлен A(x)=Q(x)x^r , где Q(x) – многочлен, отображающий комбинацию первичного кода. Ясно, что степень A(x) не ниже r , а степень R(x) не выше r – 1. Способ построения циклического кода по существу сводится к нахождению такого многочлена R(x), который, будучи прибавлен, в соответствии с (34), к многочлену A(x), давал бы многочлен, делящийся на g(x).

Такой многочлен находится делением A(x) на g(x). Через F(x) обозначается частное от деления, а остаток – через R(x)

Используя результаты деления, можно записать,

A(x) = g(x) · F(x) + R(x) (35)

Прибавляя к обеим частям равенства (35) R(x):

A(x) + R(x) = g(x) · F(x) + R(x) + R(x),

так как R(x)+R(x)=0 то A(x) + R(x) = g(x) · F(x).

Из вычислений видно, что остаток деления A(x) на g(x) и есть многочлен, представляющий поверочные символы.

Таким образом, если многочлен A(x), представляющий информационные символы умножить на x^r и прибавить остаток от деления этого многочлена на порождающий многочлен g(x), то полученный многочлен A(x) + R(x) будет делиться на g(x) без остатка. Степень полученного многочлена не превышает n–1. Следовательно, комбинация, соответствующая этому многочлену, является комбинацией циклического кода, причем информационные символы ее представлены многочленом A(x).

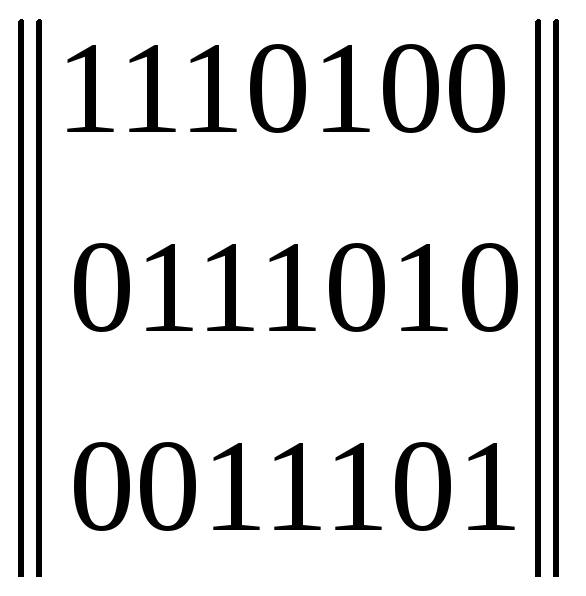
Пример. Построить циклический (7,4)-код, заданный порождающим многочленом g(x) = x³ + x + 1.

Берется любая комбинация из информационных символов: 1100. Сдвигается влево на r = 3 раза. В результате получается комбинация V_i = 1100000, представляющий ее многочлен будет

иметь вид A(x)=(x³ + x²)·x³= x⁶ + x⁵ Остаток R(x) находится делением многочлена A(x) на g(x)

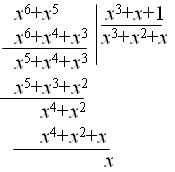
Остаток от деления будет равен R(x )= x, следовательно:

V(x) = A(x) + R(x)= x⁶+x⁵ +x

Этому многочлену соответствует следующая комбинация циклического кода: 1100010.

Естественно, при аппаратурной реализации кодера циклического кода умножение, деление и сложение многочленов осуществляется при помощи регистров сдвига с обратной связью и сумматоров по модулю 2.

Совместная работа регистра сдвига с обратной связью и сумматора по модулю 2 (рис. 4) широко используется в схемах кодирования и декодирования циклических кодов. Пример схемы, состоящей из регистра на три ячейки и сумматора по модулю 2, представлен на рис. 5 а. Так как в дальнейшем подобные и более сложные схемы будут неоднократно повторяться, эту схему заменим упрощенной схемой рис. 5 б, в которой отдельные ячейки регистра сдвига обозначены через Xⁱ, а сумматоры — знаком . Если ни в одну ячейку регистра (рис. 5, б) ничего не записано, то его состояние определится как 000. Пусть в ячейку Х° записан сигнал 1, а в ячейки X¹ и X²—0. В этом случае регистр имеет состояние 100.

Рис. 4. Логический элемент сложения по модулю 2;

а — функциональная схема; б - условное обозначение; в - таблица функционирования

Рис. 5. Работа регистра сдвига с сумматором по модулю 2 ;

а – функциональная схема ; б – условное обозначение

Если сумматор отсутствует, то получается обычный регистр сдвига и при первом переключении сигнал 1 из ячейки Х° перейдет в ячейку x и состояние регистра будет 010. В следующем такте состояние определится как 001.

Таким образом, при отсутствии сумматора по модулю 2 число состояний регистра N = n, где n — число ячеек регистра.

В каждом такте (от I до VII, исключая нулевой) показано состояние ячеек регистра после записи и считывания информации. В исходном состоянии во всех ячейках регистра записан сигнал 0. В такте I ячейку Х° регистра записывается сигнал 1. Далее вторым тактовым импульсом происходит переписывание сигнала 1 из ячейки Х° в ячейку X¹ (косая стрелка из ячейки Х° в ячейку X¹). Работа схемы представлена в табл. 5.

Таблица 5

Совместная работа регистра

и сумматора по модулю 2

В такте I I I сигнал 1 из ячейки X¹ переписывается в ячейку X² и через сумматор — в ячейку Х°, что показано соответствующими стрелками. Сигнал 1 из ячейки X² через сумматор переходит в ячейку Х°, а из ячейки Х°— в ячейку X¹ (такт IV). В такте V во всех ячейках будут записаны сигналы 1, что показано стрелками. В тактах VI и VII сумматор не пропускает два сигнала 1 с ячеек X¹ и X² в ячейку Х° и в ней записывается 0.

Сигналы 1 с ячеек Х° и X¹ переписываются в ячейки X¹ и X² соответственно (такт VI), а в такте VII 1 заполнит только ячейку X². В дальнейшем состояние ячеек регистра начнет повторяться, начиная с такта I.

Таким образом, применение сумматора позволяет увеличить число состояний схемы с трех до семи, а в общем случае до

N =2ⁿ – 1, так как нулевая комбинация никогда далее не повторяется.

Деление многочленов с помощью регистра и сумматоров. Регистр с сумматорами по модулю 2 может быть использован для деления многочлена на многочлен.

Для деления любого многочлена на заранее фиксированный многочлен

(36)

где a_i = 1 или 0, может быть использована схема рис. 6. а., в которой перед каждой ячейкой регистра имеется сумматор по модулю 2. Ячейка регистра для члена со старшей степенью и соответствующий ей сумматор отсутствуют. Это следует из процесса деления многочлена на многочлен, из которого вытекает, что старшие члены делимого и делителя, в которых всегда стоят единицы, складываясь по модулю 2, дают нуль. Для случая схема делителя представлена на рис. 6, б.Ниже приведена схема для деления на многочлен, если в нем некотораяa_i =0.

Например, если Р(Х⁶) = Х⁶+Х⁵+Х²+X+1, то сумматоры перед ячейками X³ и X⁴ регистра отсутствуют. Поэтому схема имеет вид, показанный на рис. 6, в. Однако все ячейки регистра (исключая старшую степень) в схеме присутствуют.

На схеме рис. 6, г .дан пример деления на многочлен Р(X⁴) = X⁴ +X³ + 1 (делитель). Делимым является многочлен G(X) = X⁷ + X⁵+ X⁴ + X³ + X + 1. Результат деления записан в виде табл. 6.

Из табл. 6 следует, что в такте I единица старшего разряда делимого записывается в ячейку X⁰, в такте I I эта единица считывается с ячейки X⁰ и записывается в ячейку X¹ (косая стрелка из ячейки Х° в ячейку X¹). Одновременно нуль делимого записывается в ячейку X⁰, а нули из ячеек X¹ и X² переходят соответственно в ячейки X² и X³, что также показано косыми стрелками. Нуль из ячейки X³ появляется на выходе. В тактах I I I и IV ячейки регистра продолжают заполняться, но на выход пока поступают только сигналы 0. Вследствие того что с ячейки X³ сигнал 1 через сумматор X⁰ поступает в ячейку Х° одновременно с 1 делимого, в ней записывается 0 (такт V) .

Рис. 6. Схемы деления многочлена на многочлен.

а – многочлен n – степени, б – многочлен X⁶+X⁵+X⁴+X³+X²+X+1, в – многочлен X⁶+X⁵+X²+X+1, г – многочлен X⁴+X³+1

В том же такте на выходе появляется I и через сумматор X³ происходит запись 1 в ячейку X³ (обратная связь с ячейки X³ на ячейку Х° регистра и на ту же ячейку X³ показана косыми стрелками влево и вниз). В такте VI, хотя на вход поступает 0 делимого по обратной связи с ячейки X³, в ячейку X⁰ записывается 1. Однако из-за той же обратной связи в ячейке X³ происходит запись 0, так как сумматор X³ не пропустил два сигнала 1

Заполнение ячеек регистра в такте VII происходит без обратной связи, которая вновь сказывается в такте VIII. Частное читается сверху вниз.

Таблица 6

Деление многочленов

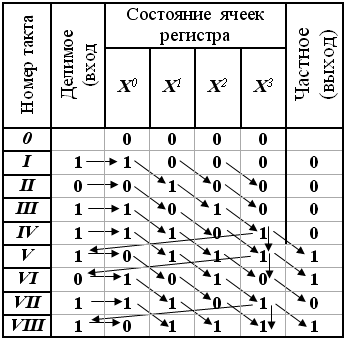
Остатки от деления начинают записываться в ячейки регистра начиная с такта V. Последний остаток 1110 записан в такте VIII.

Умножение многочленов с помощью регистра и сумматоров. Для умножения на заранее фиксированный многочлен (34) может быть использована схема, представленная на рис. 7, а). Схема умножения на многочлен X⁶+X⁵+X⁴+X³+X²+X+1 дана на рис. 7, б). На рис. 7, в) изображена схема умножителя на многочлен Р(X) =X⁴+X³+1

В табл. 7 приведен процесс умножения многочлена X⁷+X⁵+X⁴+X³+X+1 на многочлен P(X)=X⁴+X³+1. В такте I единица старшего разряда записывается одновременно в ячейки X⁰, X³ и поступает на выход. В такте II на выход проходит сигнал 1 с ячейки X³, а с ячейки X⁰ он переходит в ячейку X¹

. В такте III сигнал 1 записывается в ячейки X⁰, X³ и проходит на выход, а сигнал I с ячейки X¹ переходит в ячейку X². В такте IV сигнал 1 записывается только в ячейку X⁰, но на выход он не проходит и не записывается в ячейку X³. Этому препятствуют сигналы 1 с ячеек X² и X³.

Рис. 7. Схемы для умножения многочлена на многочлен и одночлен: а – многочлена n-степени, б – многочлена X⁶+X⁵+X⁴+X³+X²+X+1, в- многочлена X⁴+X³+1, г- одночлена X³

Начиная с такта IX информация в регистр не поступает и регистр очищается, т. е. информация, записанная в такте VIII, такт за тактом подается на выход. Результат умножения (111011010011) читается сверху вниз.

Для умножения на одночлен Xⁿ используют регистр без сумматора. Схема для умножения на одночлен X³ представлена на рис. 7, г). Пока на выход поступает множимое, ключ разомкнут и с регистра, в котором записаны нули, ничего не снимается. После поступления на выход последнего символа множимого ключ замыкается и в течение трех тактов с регистра считываются на выход три нуля, так как умножение на Xⁿ эквивалентно приписыванию к множимому n нулей справа.

Таблица 7

Умножение многочленов.

Сравнивая схемы умножителей и делителей, можно сделать следующие выводы:

1) число ячеек регистра равно старшей степени многочлена, на который происходит умножение или деление. Ячейка регистра для старшей степени многочлена отсутствует, но всегда присутствует ячейка X⁰;

2) число сумматоров на единицу меньше числа ненулевых членов многочлена, на который производится деление или умножение, или на единицу меньше его веса;

3) при делении отбрасывается сумматор, соответствующий старшему члену многочлена, а при умножении - младшему. Например, при делении на многочлен

Р(Х)=Х⁴ + Х³ + 1 остаются сумматоры для Х³, Х°, а при умножении на этот же многочлен — сумматоры до ячейки Х³ и после нее;

4) как в делителях, так и в умножителях сумматоры устанавливают перед ячейками регистра, соответствующими ненулевым членам многочлена тех же степеней. Так, в схеме умножителя на рис. 7, в) показано, что сумматор X⁴ поставлен перед отсутствующей ячейкой X⁴, а сумматор X³— перед ячейкой Х³;

5) при умножении множимое подается одновременно на вход и на все

сумматоры;

6) при делении делимое подается только на первый сумматор, а частное - на выход и на все сумматоры;

7) множимое или делимое поступает на вход начиная со старшего разряда.