К_зкзамену_ТПИ / ответы тпи

Билет№1

1.Понятие информации. Природа информации. Количественный и качественный аспект информации. Формы представления информации.

Информация техническая, которая передается по каналам связи и отображается на экранах дисплеев. Количество такой информации может быть точно вычислено, и процессы, происходящие с такой информацией, подчиняются физическим законам.

Информация семантическая, т.е. смысловая. Это та самая информация, которая содержится, к примеру, в литературном произведении. Для такой оценки информации предлагаются различные количественные оценки и даже строятся математические теории. Но общее мнение скорее сводится к тому, что оценки здесь весьма условны и приблизительны, и алгеброй гармонию все-таки не проверишь.

Информация – это физическая величина, такая же, как, например, температура или скорость. Определенным образом и при определенных условиях информация равным образом описывает как процессы, происходящие в естественных физических системах, так и процессы в системах, искусственно созданных.

Информация-совокупность сведений, опред. меру наших знаний о событиях, явлениях, фактах и тд

Информационный процесс – это любой процесс, в котором присутствует хотя бы один из элементов: передача информации, ее прием, хранение, обработка, выдача пользователю, преобразование, отображение, восприятие.

Информационная система – это любая система, реализующая или поддерживающая информационный процесс.

Количественный аспект определяет меру кол-ва информации и единицы (в чем она измер-ся (бит-осн. 1 инф.))

Качественный аспект опр-т критерий оценки инф. (полезность, содержательность.

Объектом передачи в любой системе передачи информации является сообщение, несущее какую-либо информацию.

Рис. 1.1. Функциональная схема системы передачи информации

2. Периодические и непериодические сигналы. Спектр частот периодических сигналов. Выбор ширины спектра периодических сигналов.

Простейшим периодическим сигналом является гармоническое колебание (тока, напряжения, заряда, напряженности поля), определяемое законом: s(t) = A cos(2π t/ T - ) = A cos(₁t - ), (2.1)

при -∞ < t < +∞.

Здесь A, T, ₁,   постоянные амплитуда, период, частота и фаза.

Реальные сигналы имеют начало и конец. В дальнейшем под гармоническим сигналом будет подразумеваться сигнал, определяемый функцией, совпадающей с выражением (2.1) в конечном интервале времени.

Гармоническое колебание, определяемое выражением (2.1), иногда удобно представлять в одной из следующих форм: См глава2!

s(t) = A Re [e ] = 1/2 Ae + 1/2

Первой из этих форм соответствует векторное представление, изображенное на рис. (2.2а), а второй форме – на рис. (2.2б)….

В первом случае действительная функция s(t) получается как проекция OB вектора A на его горизонтальную ось, а во втором – как сумма проекций OB на ту же ось двух векторов с амплитудами 1/2A, вращающимися с угловой частотой ₁ во взаимно противоположных направлениях.

Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов, действующих при -∞<t<+∞. Это представление осуществляется с помощью ряда Фурье.

Пусть заданная в интервале t₁<t<t₂ функция s(t) периодически повторяется с частотой ₁=2π/T, где T – период повторения (рис. 2.3), причем выполняются следующие условия (условия Дирихле):

1) в любом конечном интервале функция s(t) должна быть непрерывна или должна иметь конечное число разрывов первого рода;

2) в пределах одного периода функция s(t) должна иметь конечное число максимумов и минимумов.

Подобная функция может быть представлена рядом Фурье, который записывается в тригонометрической или комплексной формах: !!!

!Совокупность коэффициентов A_n называется спектром сигнала и полностью определяет этот сигнал.

Лекции!

Билет №2

1. Комбинаторная мера информации. Единицы измерения количества информации.

В теории информации изучаются количественные зако­номерности передачи, хранения и обработки информации. Количество информации в сообщении о некотором событии существенно зависит от вероятпости этого события. Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать монотонно убывающую функцию вероятнос См глава6!... зует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации в логариф­мических единицах, т. е. определять количество информации в отдельно взятом сообщении как:….

равно нулю, т. е. сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащееся в несколь­ких независимых сообщениях, равно сумме количества информации в каждом из них. Действительно, так как совмест что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифмак может быть любым. Чаще всего при….

Двоичную единицу называют бит. Слово "бит" произош­ло от выражения binary digit (двоичная цифра). В двоичных системах передачи информации используется два символа, ус­ловно обозначаемых 0 и 1. В таких системах пои независи…

Формула (6.1) позволяет вычислять количество инфор­мации в сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограниченно. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:….

Ансамбль сообщений образует полную группу событий, поэтому всегда:…

Отсюда следует, что количество информации в со­общении зависит от ансамбля, из которого оно выбра­но. До передачи сообщения имеется неопределенность относительно того, какое из т -сообщений ансамбля будет передано. После приема сообщения эта неопределенность снижается. Очевидно, чем больше т, тем больше неопределенность и тем большее количество информации содержится в пере­данном сообщении.

2. Коды с повторением и инверсией: процедура построения и основные характеристики.

Код с повторением и инверсией является систематическим разделимым нециклическим нелинейным (2k,k)-кодом. Имеет k информационных и r = k проверочных символов. Отличается от кода с повторением (однократным) без инверсии тем, что значение проверочных символов в нем зависят от значения сумм по модулю два всех информационных символов. Если т.е. если число единиц в информационных символах четно, то проверочные символы повторяют информационные: b_j = a_j (где j = 1 ÷ k). Если т.е. если число единиц в информационных символах нечетно, то проверочные символы повторяют информационные в обратном (инверсном) коде с заменой 0 на 1 и 1 на 0, а именно b_j = a_j Å1 (где j = 1÷ k).

Код имеет d = k при k < 4; 4,при k ≥ 4 и используется обычно для обнаружения ошибок.

Корректирующая способность кода: код позволяет обнаруживать ошибки любой кратности, за исключением таких, когда искажены два информационных символа и соответствующие им два проверочных символа, четыре информационных символа и соответствующие им четыре проверочных символа, то есть четное число информационных и соответствующие им проверочные символы.

Процедура обнаружения ошибок сводится к следующему. Одноименные информационные и проверочные символы принятой комбинации сравниваются между собой, причем, если сумма по модулю два всех информационных символов равна 0, то проверочные символы подаются в устройство сравнения в прямом коде (как были приняты), если же эта сумма равна 0, то проверочные символы подаются в указанное устройство в обратном (инверсном коде). В результате сравнения формируется синдром ошибки S = S_r S_r-1 ….S₁, S_i = 1 (i = r ÷1), если соответствующие информационные и проверочные символы в устройстве сравнения не совпадают, S_i =0, если совпадают. Значение S_i находится как сложение по модулю два i –ых информационных и соответствующих им проверочных символов.

S₁ = a₁^*Å b₁^*, S₂ = a₂^* Å b₂^*, S₃ = a₃^* Å b₃^*, при четном числе единиц в информационной части кода.

S₁ = a₁^*Å b₁^* = a₁^*Å b₁^* Å1

S₂ = a₂^*Å b₂^* = a₂^*Å b₂^* Å1

S₃ = a₃^*Å b₃^* = a₃^*Å b₃^* Å 1, при нечетном числе единиц в информационной части, где черточка над символом обозначает знак инверсии, что равносильно сложению по модулю два символа с 1, b_i^* = b_i^* Å1.

Относительная скорость передачи q = k/n = k/2k =1/2

Избыточность кода И = n-k/k = 2k - k/k = 1

Вероятность появления ошибок комбинации на выходе устройства обнаружения ошибок при одноразовой передаче комбинации по двоичному симметричному каналу (ДСК) или вероятность необнаружения ошибок равна вероятности появления четного числа (2,4,6 …) ошибок в информационной части кода и соответствующих им ошибок в проверочной части кода:

P_{ош. пр}= P_н.ош = C²_k p² q^k-2 p² q^k-2+ C⁴_k p⁴ q^k-4 p⁴ q^k-4+…….

Вероятность обнаружения ошибок равна:

P_{о ош.}= P_ош - P_н.ош, P_ош = 1-qⁿ, q = 1-p, где P_ош – вероятность искажения кодовой комбинации. qⁿ – вероятность правильного приема кодовой комбинации длины n, q – вероятность правильного приема одного символа. p – вероятность искажения одного символа.

Пример построения кода с повторением и инверсией при N=8, k=3 (2^k=2³=8, N=2^k), r=k=3, n=k+r=3+3=6

Процедура построения:

Строится первичный (обычный двоичный) код длины k=3, который будет являться информационной частью корректирующего кода. Затем с правой стороны приписываются проверочные символы, являющиеся повторением информационных символов, в случае если в информационной части четное число единиц. Если в информационной части нечетное число единиц, проверочные символы записываются в инверсном виде. Построение корректирующего кода отражено в таблице. См в лабах!

Характеристики кода

1. Код разделимый

2. Число информационных символов k=3

3. Число проверочных символов r=3

4. Длина кода n = k+ r= 3+3 = 6

5. Кодовое расстояние d=3

6. Корректирующая способность кода – код обнаруживает все ошибки за исключением одновременного искажения a₁, a₂, и b₁, b₂; a₃ и b₃, a₁,a₃ и b₁ , b₃; a₂ ,a₃ и b₂ , b₃ и др.

7. Процедура обнаружения и формирования синдрома ошибки рассмотрим на следующих примерах:

1. передавалась комбинация 110110. В процессе передачи искажен первый символ, вектор ошибки e=100000. Принята комбинация 010111. В информационной части нечетное число единиц. Инвертируем проверочную часть и анализируем полученную комбинацию 010000. Находим синдром ошибки S

S₁ = a₁Å b₁ = 0Å0 =0

S₂ = a₂Å b₂ = 1Å0 =1

S₃ = a₃Å b₃ = 0Å0 =0.

Откуда S =010, указывает на наличие ошибки.

2. передавалась комбинация 110110. В процессе передачи искажены первые и третьи символы как в информационной так и в проверочной части. Вектор ошибки 101101. Полученная комбинация 011011. В информационной части четное число единиц. Инверсирование не требуется. Анализируем принятую комбинацию и находим синдром S.

S₁ = a₁Å b₁ = 1Å1 =0

S₂ = a₂Å b₂ = 0Å0 =0

S₃ = a₃Å b₃ = 1Å1 =0.

Синдром S=000 указывает, что ошибки нет. Но на самом деле имеется ошибка четвертой кратности, но она не обнаруживается и осуществляется ошибочный прием.

Относительная скорость передачи q=k/n = 3/6 = ½,Избыточность И = n-k/k = 1,Вероятность появления ошибочной комбинации на выходе приемного устройства равна вероятности необнаруживаемой ошибки.Р_{н о} = С²₃ p² q^3-2 p² q^3-2= С²₃ p⁴ q²

Примем p = 10^-3, тогда q=1-10^-3 = 0, 999

Р_{н о} = 3∙(10^-3 )⁴(0,999)² =3∙10^-12 0,998 = 2,994∙10^-12

Вероятность отсутствия ошибки равна qⁿ = 0,999⁶. Вероятность искажения символов от однократных до шестикратных равно:P_1-6 = С¹₆ p¹ q⁵ + C²₆ p² q⁴ + C³₆ p³ q³ + C⁴₆ p⁴ q²+ C⁵₆ p⁵ q¹+ C⁶₆ p⁶ q⁰ = 6∙^10-3 0,999⁵ +15∙ (10^-3)² ∙ (0,999)⁴ + 20∙(10^-3)³ (0,999)³ +15∙ (10^-3)⁴ ∙0,999² +6(10^-3)¹⁵ ∙ (0,999)⁵ + (10^-3)⁶≈

Билет№3

1. Энтропия ансамбля случайных событий. Основные свойства энтропии ансамбля случайных событий. Лекции!

Величина Н(а) называется энтропией. Этот термин за­имствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность со­стояния физической системы. В теории информации энтро­пия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Для нас самым существенным является то, что чем больше эн­тропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

2. Код с проверкой на четность: процедуры построения и основные характеристики.

Этот код является простейшим разделимым систематическим циклическим линейным кодом длины n с k = n-1 информационными и r = 1 проверочным символом. Обозначается как (n, n-1)-код. Его комбинации обладают свойством цикличности, поэтому код является циклическим.

В рамках ТЛ3 проверочный символ находится как сумма по модулю два всех информационных символов !111

При таком способе нахождения b₁ число единиц в любой кодовой комбинации кода четно. Код имеет d = 2 и применяется для обнаружения ошибки.

Корректирующая способность кода: код обнаруживает ошибки любой нечетной кратности в пределах n.

Процедура обнаружения состоит в проверке на четность всей принятой комбинации. Результат этой проверки характеризуется одним символом синдрома S: S = S₁

!!!

где a_i*, b_i* - значения информационных и проверочных символов в принятой кодовой комбинации.

Считается, что если S₁ = 0, то комбинация принята без ошибок (ошибки нет или есть ошибки четной кратности), если S₁ =1, то комбинация принята с ошибками.

Относительная скорость передачи q = k/n .

Избыточность кода И = 1/k.

Вероятность появления ошибочной комбинации на выходе устройства обнаружения ошибок при одноразовой передаче комбинации по двоичному симметричному каналу (ДСК) равно вероятности появления ошибок четной кратности:

Вероятность обнаружения ошибок равно вероятности появления ошибок нечетной кратности:

Пример построения кода с проверкой на четность при N = 8, k = 3 (2³ = 8) и r = 1.

Процедура построения: Строится первичный (обычный двоичный) код длины k=3, затем с правой стороны приписывается 1 или 0 по правилам, изложенным выше. Построение кода с проверкой на четность отражено в таблице.!1!1

Характеристики кода

1. Код разделимый

2. Число информационных символов k=3

3. Число проверочных символов r=1

4. Длина кода n = k+r = 3+1= 4

5. Кодовое расстояние d=2

6. Корректирующая способность кода – код обнаруживает однократные и трехкратные ошибки

7. Процедуру обнаружения и формирования синдрома ошибки рассмотрим на следующих примерах:

   1. передавалась комбинация 0110, принята комбинация 1110 (искажен первый символ). Синдром ошибки S₁ =1 Å 1 Å 1 Å 0 = 1, S = 1 – ошибка есть и обнаружена

   2. передавалась комбинация 0110, принята комбинация 1010, искажены первый и второй символы. Синдром ошибки S₁ =1 Å 0 Å 1 Å 0 = 0, S = 0 – ошибка есть, но она не обнаружена

8. Относительная скорость передачи q = k/n = ¾

9. Избыточность кода И = 1/k = 1/3

10. Вероятность появления ошибочной комбинации на выходе устройства обнаружения при вероятности перехода 1 в 0 и 0 в 1. р=10^-5 и вероятности приема неискаженных символов q=1-p=1-10^-5 равна:

Р_ош = С²_n p² q^n-2 + C⁴_n p⁴ q^n-4 = С²₄ p² q^4-2 + C⁴₄ p⁴ q^4-4 = 6∙(10^-5)²∙(1-10^-5)² +

1∙ (10^-5)⁴(1-10^-5)⁰ ≈ 6∙10^-10

Вероятность необнаружения однократных и трехкратных ошибок:

Р_но = С¹_n p¹ q^n-1 + C³_n p³ q^n-3 = 4∙p q^4-1 +4∙p³ q^4-1 = 4∙10^-5 (1-10^-5)³ + 4∙ (10^-5)³∙ (1-10^-5)⁰ 4∙10^-5

Билет №4.

1. Система с информационной обратной связью.

Системами с информационной обратной связью (ИОС) называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения:

1)повторить ошибочно принятые отрезки сообщения;

2)изменить применяемый код (передав предварительно соответствующий условный сигнал и убедившись в том, что он принят);

3)прекратить передачу при плохом состоянии канала до его улучшения.

2. Линейный код, построенный на основе теории матриц

Двоичный (n,k) код наз.линейным, если все его (2ˆk -1) ненулевых комбинаций явл. суммами по модулю 2, строк некоторой матрицы G размером (k×n). Матрица называется порождающая

Билет №5.

1. Энтропия непрерывной случайной величины. Основные свойства энтропии непрерывной случайной величины.

При передаче непрерывных сообщений переданные сиг­налы s(t) являются функциями времени, принадлежащими..

некоторому множеству, а принятые сигналы будут x(t) их искаженными вариантами. Все реальные сигналы имеют спек­тры, основная энергия которых сосредоточена в ограничен­ной полосе F. Согласно теореме Котельникова такие сигналы определяются своими значениями в точках отсчета, выбирае..

В канале на сигнал накладываются помехи, вследствие чего количество различных уровней сигнала в точках отсчета будет конечным. Следовательно, совокупность значений не­прерывного сигнала эквивалентна некоторой дискретной ко­нечной совокупности. Это позволяет нам определить необхо­димое количество информации и пропускную способность ка­нала при передаче непрерывных сообщений на основании ре­зультатов, полученных для дискретных сообщений.

Определим количество информации, которое содержится в одном отсчете сигнала x_i относительно переданного сигнала S_i. Это можно сделать на основании соотношения (6.36), если в последней вероятности выразить через соответствующие…

Необходимо отметить, что, в отличие от энтропии диск­ретных сигналов, величина дифференциальной энтропии за­висит от размерности непрерывного сигнала. По этой при­чине она не является мерой количества информации, хотя и характеризует степень неопределенности, при­сущую источнику.

2. Линейные (h,k)- коды. Задание линейного кода при применении теории линейных зависимостей. Свойства линейный кодов.

В классе блоковых разделимых корректирующих кодов различают коды систематические и несистематические. Систематическим называют такой код, в комбинациях которого информационные символы занимают первые k позиций, а проверочные – последние r = n-k позиций. Если информационные символы обозначать через a_i(I = 1÷k), а проверочные – через bi(j = 1÷r), то любая комбинация V симметрического кода, согласно определению, должна иметь структуру V = (a₁a₂ … a_kb₁b₂ … b_r)При ином расположении информационных и проверочных символов код называется несистематическим. Остановимся на рассмотрении систематических линейных кодов в рамках теории линейных зависимостей.Двоичный (n,k) – код называется линейным, если его проверочные символы b_j (j = 1 ÷ r) находятся как суммы по mod2 определенных информационных символов a_i (i = 1 ÷ k). _k

b_j = ∑0 C_ji a_i,

i=1

где ∑0 - символ суммирования по mod2. C_ji - коэффициенты, могущие принимать значения либо 0, либо 1.

b_i= C_j1a₁Å C_j2a₂Å ….. Å C_jka_k, b₁= C₁₁a₁Å C₁₂a₂Å ……… C_1кa_к ,

b₂= C₂₁a₁Å C₂₂a₂Å ……… C_2кa_к ,

b_r= C_r1a₁Å C_r2a₂Å ……… C_rкa_к ,

Операция сложения по mod2 является линейной операцией, отсюда и название кода.

Если проверочные символы определяются по другому правилу, то (n,k)-код называется нелинейным.

Закон построения линейного кода задается совокупностью коэффициентов C_ji , число которых k_r .

Пример1. Построить линейный (7,4)-код, заданный следующей совокупностью коэффициентов C_ji (всего таких коэффициентов должно быть задано 4·3=12): i=(1÷4), j=(1-3)

С₁₁=1 С₁₂=1 С₁₃=0 С₁₄=1

С₂₁=1 С₂₂=0 С₃₃=1 С₂₄=1

С₃₁=0 С₃₂=1 С₃₃=1 С₃₄=1

Проверочные символы находятся по формулам:

_k

b_j = ∑⁰ C_ji a_i,

i=1

b₁= ∑0C_jia_i = C₁₁a₁ÅC₁₂a₂ÅC₁₃a₃ÅC₁₄a₄=1∙a₁Å1∙a₂Å0∙a₃Å1∙a₄ = a₁Åa₂Åa₄

b₂= ∑0C_jia_i = C₁₁a₁ÅC₁₂a₂ÅC₁₃a₃ÅC₁₄a₄=1∙a₁Å0∙a₂Å1∙a₃Å1∙a₄ = a₁Åa₃Åa₄

b₃= ∑0C_jia_i = C₁₁a₁ÅC₁₂a₂ÅC₁₃a₃ÅC₁₄a₄=0∙a₁Å1∙a₂Å1∙a₃Å1∙a₄ = a₂Åa₃Åa₄

Cтроим первичный код с числом комбинаций N=2^k = 16 и записываем его в таблицу графы 2,3, 4,5. По приведенным формулам определяем проверочные символы и записываем их в графы 6,7,8 таблицы. В графу 8 записывается вес полученных кодовых комбинаций. Например, первичная комбинация a₁a₂a₃a₄ = 1001, b₁ = a₁Åa₂Åa₄ = 1Å0Å1=0, b₂ = a₁Åa₃Åa₄ = 1Å0Å1=0, b₃=a₂Åa₃Åa₄=0Å0Å1=1. Корректирующий код 1001001. Вес этой комбинации w=3 (9 комбинация из таблицы)!!11

В таблице представлены все N = 2⁴=16 комбинаций кода.

Нетрудно убедиться в том, что построенный код имеет d == 3. Для другой совокупности коэффициентов C_ji был бы получен другой линейный код с тем же или иным d.

Отметим два интересных свойства линейных кодов.

1. Сумма по mod2 любых двух комбинаций линейного кода снова дает комбинацию этого же кода. В справедливости этого легко убедиться, сложив любые две комбинации построенного в предыдущем примере кода.

2. Кодовое расстояние d линейного кода равно минимальному весу его ненулевых комбинаций. Проставив в предыдущем примере справа веса всех комбинаций, убедимся, что d= w_min=3. Это свойство дает очень простой способ определения кодового расстояния для любого линейного (n,k)-кода.

Характеристики систематического (n,k)-кода на примере (7,4)-кода с совокупностью коэффициентов C_ji, приведенных выше, n=7, k=4, r =n·k=3.

1. Код разделимый, длина кода – n=7.

2. Число информационных символов k =4, число проверочных символов r = n-k = 7-4 =3.

3. Кодовое расстояние d = 3, равно минимальному весу его ненулевых комбинаций.

4. Избыточность кода U = n-k/k = 7-4/4 = ¾.

5. Корректирующая способность кода. Код обнаруживает все однократные и двухкратные ошибки и некоторые ошибки большей кратности. Код исправляет однократные ошибки.

6. Процедура обнаружения и исправления ошибок.

Обнаружение ошибок в комбинациях линейных кодов.

Пусть передана комбинация V = (a₁a₂ … a_kb₁b₂ … b_r), а принята комбинация V* = (a₁*a₂* … a_k*b₁*b₂* … b_r*).

В общем случае из-за возможных искажений не все одноименные символы этих комбинаций совпадают.

По принятым информационным символам на приемной стороне вычисляются проверочные:

_k

b*_j* = ∑0 C_ji a_i^*,

i=1

Вычисленные значения сравниваются с принимаемыми символами b_j*. Это сравнение можно осуществить путем операции сложения по mod2:

S_j = b_j*b_j* , j = 1÷r

Результаты сравнения можно представить в виде набора из r символов (S_rS_r-1 … S₂ –S₁). Ясно, что если для всех j сравнение показало совпадение вычисленного и полученного проверочного символа (b_j** = b_j*), то это свидетельствует об отсутствии искажений в принятой комбинации. Иными словами, если r – элементная комбинация (S_r … S_r S₁) состоит из одних нулей, то ошибки нет; если хотя бы один символ в этом наборе принял значение 1, то это говорит о наличии ошибок в принятой комбинации. Поэтому набор символов S=(S_r … S₁) называют синдромом или опознавателем ошибок.

Пример2: Пусть была передана комбинация кода V=1001001, а принята V₁* = 1001011, V₁* = a₁*a₂*a₃*a₄*b₁*b₂*b₃*.

Тогда b₁** = a₁*a₂*a₄* = 101=0

b₂** = a₁*a₃*a₄* = 101=0

b₃** = a₂*a₃*a₄* = 001=1

Сравнение вычислительных символов с принятыми проверочными дает:

S₁ = b₁** b₁* = 00=0

S₂ = b₂** b₂* = 01=1

S₃ = b₃** b₃* = 11=0

Т.е. получен ненулевой синдром S = 010, что свидетельствует об ошибке в принятой комбинации.

Процесс исправления ошибок осуществляется аналогичным способом. Полученный ненулевой синдром, ввиде трехзначного двоичного кода указывает позицию, на которой произошла ошибка. Исправление ошибки заключается в замене принятого значения символа на инверсный (0 на 1 или 1 на 0).

Для рассматриваемого кода соответствие между номером позиций и значением синдрома следующие: !!!

7. Относительно скорости передачи q = k/n = 4/7

8. Верность передачи определяется как вероятность обнаружения ошибки, при использовании (n,k)-кода в качестве обнаруживающего ошибку, или как вероятность исправления одиночной ошибки, при использовании (n,k)-кода в качестве исправления одиночной ошибки.

P_обн. = C^|_n P^|q^n-1 + C²_n P² q^n-2 – вероятность обнаружения 1 и 2^х кратных ошибок

P_исп. = C^|_n P^| q^n-1 – вероятность исправления ошибок.

Рассмотрим два линейных (n,k)-кода, получивших название кодов Хэмминга по имени разработчика. Один из которых является систематическим, второй – несистематическим.

Систематический линейный (n,k)-код

Для (7,4)-кода N=16

Запишем все восемь вариантов.

Значения каждого из проверочных символов b_i при построении кодовых комбинаций определяется путем сложения по mod2 определенных информационных символов. b_i =0, если сумма равна 0; b_i =1, если сумма равна 1. Если использовать для определения b₁ символы a₁a₂a₄, b₂ - a₁a₃a₄, b₃ – a₂a₃a₄, а именно b₁ = a₁Åa₂Åa₄, b₂ = a₁Åa₃Åa₄, b₃ = a₂Åa₃Åa₄. То это дает возможность получить номер позиции с искаженным символом записанной комбинацией двоичного кода (двоичного числа, а именно):

Код имеет d=3 и применятся для обнаружения ошибок исправления однократной ошибки.

Таблица кодовых комбинаций корректирующего кода приведена ниже!

Билет №6.

1. Количество информации в случае ансамбля случайных событий, непрерывной случайной величины.

Лекции!

2. Коды, применяемые в АЦП. Двоичный, двоично-десятичный, код Грея.

Смещенный код применяется в блоках АЦП и ЦАП.

Двоично-десятичный код применяется в системах индикации и т.п.

Каждый десятичный разряд кодируется группой из 4 двоичных разрядов.

Пример:

Код Грея используется в механических шифраторах угла поворота вала. При переходе из любого его состояния к следующему изменяется лишь один разряд. Это позволяет предотвратить ошибки, так как в данном случае при переходе между двумя соседними значениями все разряды не могут измениться одновременно.

(0000) (1100)

(0001) (1101)

(0011) (1111)

(0010) (1110)

(0110) (1010)

(0111) (1011)

(0101) (1001)

(0100) (1000)

Билет №7.

1. Способы обнаружения ошибки в комбинациях линейного (h,k)- кода. Понятие синдрома. См билет5(2)+ Определение синдрома

2. Классификация корректирующих кодов.

Билет16(2)

Билет №8.

1. Основные характеристики устройств передачи информации (помехоустойчивость, эффективность, своевременность).

Помехоустойчивость технического устройства (системы), способность устройства (системы) выполнять свои функции при наличии помех. П. оценивают интенсивностью помех, при которых нарушение функций устройства ещё не превышает допустимых пределов. Чем сильнее помеха, при которой устройство остаётся работоспособным, тем выше его П. Требования к П. различных устройств отличаются большим разнообразием: Часто понятие «П.» применяют для характеристики устройств передачи информации (например, линий связи). Для них в большинстве случаев может быть определено понятие «сигнал», и оценка П. может производиться на основе рассмотрения соотношения между помехой и сигналом, при котором обеспечивается заданное качество функционирования.

Так как действие помехи проявляется в том, что принятое сообщение отличается от переданного, то количественно помехоустойчивость при заданной помехе можно характеризовать степенью соответствия принятого сообщения переданному. Назовем эту величину общим термином – достоверность. Количественную меру достоверности приходится выбирать по-разному, в зависимости от характера сообщения.

Наряду с достоверностью (помехоустойчивостью) важнейшим показателем работы системы передачи информации является скорость передачи.

В системах передачи дискретных сообщений скорость измеряется числом передаваемых двоичных символов в секунду R. Для одного канала двоичная скорость передачи определяется соотношением:

1

R = — log m,

₀

где ₀ – длительность элементарной посылки сигнала, m – основание кода.

2.Назначение и основная идея построения корректирующих кодов.

Корректирующие коды строятся так, что для передачи сообщения используются не все кодовые комбинации mⁿ, а лишь некоторая часть их (так называемые разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации дополнительных (избыточных) символов.

Билет №9

1. Вероятностная теория информации. Понятие энтропии и количества информации.

Главной отличительной особенностью вероятностного подхода от комбинаторного является тот факт, что он основан на вероятностных допущениях относительно пребывания какой-либо системы в различных состояниях. При этом общее число элементов (микросостояний, событий) системы не учитывается. За количество информации здесь принимается снятая неопределенность выбора из множества возможностей, имеющих, в общем случае, различную вероятность. Основополагающая роль в вероятностном подходе принадлежит энтропии (Н) множества вероятностей.

Теорема: Множество возможных событий, вероятности осуществления которых суть . Существует единственная функция Н, удовлетворяющая трем свойствам:

1. Н должна быть непрерывной относительно .

2. Если все равны, то Н должна быть монотонно возрастающей функцией от n.

3. Если выбор распадается на два последовательных выбора, то первоначальная Н должна быть взвешенной суммой индивидуальных значений Н каждого из выборов.

При этом Н имеет вид:

,где К – некоторая положительная постоянная.

2. Модуляция и демодуляция. Основные понятия. Виды модуляции

Передача сообщений по каналу связи осуществляется с помощью некоторого физического процесса, который называется переносчиком. В системах передачи информации переносчиком является электрическое колебание. Всякий сигнал получается путем модуляции. Немодулированный переносчик не несет информации – он подобен чистому листу бумаги, в то время как модулированный переносчик можно сравнить с листом бумаги, на котором написаны буквы и знаки, отображающие информацию.

Модуляция состоит в том, что один из параметров переносчика f(a, b, c, …) изменяется во времени в соответствии с передаваемым сообщением u(t). Если изменяется (модулируется) параметр c, то получается c-модуляция, если изменяется параметр b, то получается b-модуляция, и т.д. Модулированные сигналы различаются переносчиками и модулируемыми параметрами. Число возможных видов модуляции при данном виде переносчика определяется числом его параметров

Восстановление переданного сообщения в приемнике обычно осуществляется в такой последовательности. Сначала производится детектирование сигнала. Цель этой операции состоит в извлечении из модулированного сигнала модулирующего сигнала. При этом производятся действия, обратные операции модуляции, поэтому детектирование называют демодуляцией.

Общий принцип модуляции состоит в изменении одного или нескольких параметров несущего колебания (переносчика) f(а,b,...,t) в соответствии с передаваемым сообщением. Так, например, если в качестве переносчика выбрано гармоническое колебание , то можно образовать три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ). Если переносчиком является периодическая последовательность импульсов, то при заданной форме импульсов можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), время-импульсную (ВИМ, ФИМ) и частотно-импульсную (ЧИМ).

Билет №10.

1. Квантование непрерывных величин. Квантование непрерывных функций. Цель квантования. Равномерное и неравномерное квантование. Интервал квантования.

Переход от аналогового представления сигнала к цифровому, который дает в ряде случаев значительные преимущества при передаче, хранении и обработке информации, связан с дискретизацией сигнала х(t) по времени и с квантованием по уровню.

Рассмотрим разновидности сигналов, которые описываются функцией х(t).

Рис. 4.1. Виды сигналов: а) непрерывный сигнал;б) дискретный по времени сигнал; в) сигнал, квантованный по уровню;г) цифровой сигнал глава4!

Непрерывная функция непрерывного аргумента (непрерывный сигнал, рис. 4.1а). В этом случае значения, которые может принимать функция x(t) и аргумент t, заполняют конечные (или бесконечные) промежутки [0, X] и [0, T] соответственно.Непрерывная функция дискретного аргумента (дискретный во времени сигнал, рис. 4.1б). Здесь значения функции x(t) определяются лишь на дискретном множестве значений аргумента t_i, i=0, 1, 2, …, (0<t<T).

Дискретная функция непрерывного аргумента (квантованный по уровню сигнал, рис. 4.1в). В этом случае значения, которые может принимать функция x(t), образуют дискретный ряд чисел x₁, x₂, …, x_k, …, т.е. такой конечный или бесконечный ряд, в котором каждому числу можно поставить в соответствие интервал (a_k, b_k), внутри которого других чисел данного ряда нет. Значение аргумента t может быть любым на отрезке [0, T].

Дискретная функция дискретного аргумента (цифровой сигнал, рис. 4.1г). Значения, которые могут принимать функция x(t) и аргумент t, образуют дискретные ряды чисел x₁, x₂, …, x_k, … и t₀, t₁, t₂, …, t_i, …, заполняющие отрезки [0, X] и [0, T] соответственно.

Дискретизация состоит в преобразовании сигнала x(t) непрерывного аргумента t в сигнал x(t_i) дискретного аргумента t_i.

Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала x(t_i) в дискретное множество значений x_k, k=0, 1, 2, …, m-1.

Совместное применение операций дискретизации и квантования позволяет преобразовать непрерывный сигнал x(t) в дискретный по координатам x и t.

Применительно к детерминированной функции рассмотрим сущность понятия дискретизации сигнала x(t).

Квантование сигнала x(t) по уровню состоит в преобразовании непрерывных значений сигнала x(t_i) в моменты отсчета t_i в дискретные. В результате квантования по уровню непрерывное множество значений сигнала x(t_i) разбивается на m одинаковых частей – интервалов квантования. Под порогом (интервалом) квантования _k понимается разность:

_k=x_k – x_k-1,

где x_k-1, x_k – соседние уровни квантования.

Шкала x значений сигнала x(t) может быть разбита на отдельные участки различным образом: с привязкой уровней квантования x_k к точке x(t)=0, к границам x_min, x_max диапазона изменения сигнала и т.д.

Обычно применяются следующие способы отнесения значений сигнала x(t_i) к соответствующему уровню квантования:

а) сигнал x(t_i) отождествляется с ближайшим уровнем квантования;

б) сигнал x(t_i) отождествляется с ближайшим меньшим (или большим) уровнем квантования.

Рис. 4.7. Варианты отождествления сигнала с уровнями квантования

Для сигнала x₁(t), показанного на рис. 4.7а, по первому способу отождествления x₁(t_i)x_k, а по второму x₁(t_i)x_k-1. Для второго сигнала в обоих случаях x₂(t_i)x_k-1 (рис. 4.7б).

Так как в процессе квантования по уровню значение сигнала x отображается уровнем квантования x_k , а каждому уровню x_k может быть поставлен в соответствие свой номер (число), то при передаче или хранении можно вместо истинного значения уровня квантования x_k использовать соответствующее число k. Истинное значение уровня квантования легко восстановить, зная масштаб по шкале x.

Устройство для квантования сигнала по уровню, называемое квантизатором (рис. 4.8а), представляет собой нелинейный элемент с амплитудной характеристикой типа приведенной на рис. 4.8б при отождествлении сигнала с ближайшим меньшим уровнем квантования или типа приведенной на рис. 4.8в в случае отождествления сигнала с ближайшим уровнем.

Рис. 4.8. К определению максимальной погрешности квантования по уровню

а) – устройство квантования; б) – квантование отождествления сигнала с низшей

границей интервала; в) – квантование с отнесением сигнала к середине интервала

Квантование по уровню сопровождается шумами квантования, или погрешностью квантования. Погрешность квантования x_k=x(t_i) – x_k связана с заменой истинного значения сигнала x(t_i) уровнем квантования x_k . Максимальная погрешность квантования зависит от способа отождествления сигнала с уровнем квантования. Для первого из рассмотренных способов она равна (рис. 4.8б):

maxx_k=maxx(t_i) - x_k = _k. (4.23)

При отождествлении с ближайшим уровнем квантования максимальная погрешность (рис. 4.8в) не превышает 0.5_k, т.е. способ квантования по уровню, отождествляющий сигнал с ближайшим квантованным уровнем, приводит к снижению максимальной погрешности квантования.

В заключение можно сказать, что преобразование непрерывного сообщения в цифровое состоит из трех операций: сначала непрерывное сообщение подвергается дискретизации во времени через интервал t; полученные отсчеты мгновенных значений x(nt) квантуются с шагом ; наконец, последовательность квантованных значений передаваемого сообщения представляется посредством кодирования в виде последовательности m-ичных кодовых комбинаций.

Такое преобразование называется импульсно-кодовой модуляцией (ИКМ).

2. Кодирование, код, декодирование. Цифровые и нецифровые коды. Характеристики кодов.

Преобразование дискретного сообщения в сигнал состоит из двух операций: кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция – вид формируемого сигнала, который должен передаваться по каналу связи.

Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Для европейских языков число элементов колеблется от 52 до 55, для восточных языков оно может исчисляться сотнями и даже тысячами. Так как число элементов в дискретном сообщении конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел.

Так, для передачи букв русского алфавита (их 32) необходимо передавать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача десяти цифр от 0 до 9. Практически для этого нужно передавать по каналу связи десять сигналов, соответствующих различным цифрам. Систему передачи дискретных сообщений можно существенно упростить, если воспользоваться при кодировании двоичной системой счисления.

В десятичной системе основанием счисления является число 10. Поэтому любое число N можно представить в виде:

N = …+a₂10²+a₁10¹+a₀10⁰,

где a₀, a₁, …, a_n – коэффициенты, принимающие значения от 0 до 9. Так, число 265 можно записать так:

210²+610¹+510⁰.

Очевидно, в качестве основания счисления можно принять любое целое число m и представить число N как:

N = …+a₂m²+a₁m¹+a₀m⁰,

где a₀, a₁, …, a_n – коэффициенты, принимающие значения от 0 до m-1. Задаваясь величиной m, можно построить любую систему счисления. При m=2 получим двоичную систему, в которой числа записываются при помощи всего лишь двух цифр: 0 и 1:

13: 8+4+1: 12³+12²+02¹+12⁰: 1101,

15: 8+4+2+1: 12³+12²+12¹+12⁰: 1111,

16: 16: 12⁴+02³+02²+02¹+02⁰: 10000,

20: 16+4: 12⁴+02³+12²+02¹+02⁰: 10100.

Арифметические действия в двоичной системе весьма простые. Так, сложение осуществляется по следующим правилам:

0+0=0; 0+1=1; 1+0=1; 1+1=10.

Различают еще символическое поразрядное сложение без переноса в высший разряд, так называемое «сложение по модулю два». Правила этого сложения следующие:

00=0; 01=1; 10=1; 11=0.

Если преобразовать последовательность элементов сообщения в последовательность двоичных чисел, то для передачи последних по каналу связи достаточно передавать всего лишь два кодовых символа: 0 и 1. Практическая реализация такой передачи очень проста: символы 0 и 1 могут передаваться колебаниями с различными частотами или посылками тока разной полярности.

При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией.

Совокупность кодовых комбинаций, обозначающих дискретные сообщения, называется кодом. Правило кодирования обычно выражается кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество – основанием кода. В общем случае при основании кода m правила кодирования N элементов сообщения сводятся к правилам записи различных чисел в m-ичной системе счисления. Число символов n, образующих кодовую комбинацию, называется значностью кода или длиной кодовой комбинации.

В зависимости от системы счисления, используемой при кодировании, различают двухпозиционные и многопозиционные коды. К первым относятся все коды, в которых используется двоичная система счисления. Часто эти коды называют двоичными. К многопозиционным кодам относятся все коды, в которых число позиций (основание кода) больше двух. Различают коды равномерные и неравномерные.

Равномерными называются такие коды, у которых все кодовые комбинации имеют одинаковую длину. Для равномерного кода число возможных кодовых комбинаций равно mⁿ. Примером такого кода является пятизначный код Бодо. Этот код содержит пять двоичных элементов (m=2; n=5). Число возможных кодовых комбинаций равно 2⁵=32, что достаточно для кодирования букв алфавита.

Кодовая таблица представлена в табл. 1.1. см глава!

Символ 1 передается положительным импульсом длительности , а символ 0 – отрицательным импульсом той же длительности. Время передачи любой кодовой комбинации равно 5₀. Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.

Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов 0 и 1, но и их количеством. Это приводит к тому, что различные кодовые комбинации имеют разную длительность.

Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются только в двух сочетаниях: как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам – тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями.

Кодовая таблица представлена в табл. 1.2.

Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называются соответственно кодером и декодером. Как правило, это нелинейные логические устройства. Устройства, преобразующие код в сигнал (модулятор) и сигнал в код (демодулятор), принято называть модемами.

В системах передачи дискретных сообщений в результате демодуляции последовательность элементов сигнала превращается в последовательность кодовых символов, после чего эта последовательность преобразовывается в последовательность элементов сообщения, выдаваемую получателю (рис.1.5). Это преобразование называется декодированием.

Билет №11

1. Дискретизация непрерывных функций. Шаг дискретизации. Равномерная и непрерывная дискретизация.

+см билет 10 (1)

Дискретизация реализации сигнала x(t) связана с заменой промежутка изменения независимой переменной некоторым множеством точек, т.е. операции дискретизации соответствует выражение:

x(t)  x(t_i), (4.1)

где x(t) – функция, описывающая сигнал;

x(t_i) – функция, описывающая сигнал в результате дискретизации.

Следовательно, в результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(t_i).

По значениям функции x(t_i) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функцию, полученную по результатам восстановления (интерполяции) по значениям x(t), будем называть воспроизводящей и обозначим через V(t).

Воспроизводящая функция V(t) строится как взвешенная сумма некоторого ряда функций f(t – t_k):

V(t) =  a_kf(t – t_k), (4.2)

k

причем коэффициенты a_k зависят от отсчетов x(t_i), x(t_i-1), …

При обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям x(t_i) можно было получить воспроизводящую функцию V(t), которая с заданной точностью отображает исходную функцию x(t).

При дискретизации сигналов приходится решать вопрос о том, как часто следует производить отсчеты функции, т.е. каков должен быть шаг дискретизации t_i=t_i – t_i-1.

При малых шагах дискретизации t_i количество отсчетов функции на отрезке обработки будет большим и точность произведения – высокой. При больших t_i количество отсчетов уменьшится, но при этом, как правило, снижается точность восстановления.

Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборок. В этом случае все отсчеты существенны для восстановления исходного сигнала. При неоптимальной дискретизации кроме существенных отсчетов имеются и избыточные отсчеты.

Избыточные отсчеты не нужны для восстановления сигнала с заданной точностью. Они загружают тракт передачи информации, отрицательно сказываются на производительности обработки данных ЭВМ, вызывают дополнительные расходы на хранение и регистрацию данных. В связи с этим актуальна задача сокращения избыточности данных. Сокращение избыточности для получателя информации может производиться в процессе дискретизации сигналов. В более общем плане задача сокращения избыточных отсчетов может рассматриваться как задача описания непрерывных сигналов с заданной точностью минимальным числом дискретных характеристик.

Методы дискретизации и восстановления сигналов можно разделить на несколько групп в зависимости от принятых признаков классификации. Выберем для классификации следующие признаки:

регулярность отсчетов;

критерий оценки точности дискретизации и восстановления;

базисные функции;

принцип приближения.

Регулярность отсчетов

В процессе дискретизации отрезок обработки сигнала x(t) разбивается на ряд не перекрывающихся интервалов t₁, t₂, t₃, …

В соответствии с признаком регулярности отсчетов можно выделить две основные группы методов: равномерную и неравномерную дискретизацию (соответственно и восстановление).

Дискретизацию будем называть равномерной, если длительность интервалов: t₁ = t_i – t_i-1 = t = const на всем отрезке обработки [0, T] сигнала.

Шаг дискретизации t, или частота отсчетов F₀ = 1/t, выбираются на основе априорных сведений о характеристиках сигнала x(t). При использовании методов равномерной дискретизации приходится решать в числе остальных вопрос о выборе частоты отсчетов (шага дискретизации) и способа восстановления сигналов.

Методы равномерной дискретизации нашли широкое применение. Это объясняется тем, что алгоритм дискретизации и восстановления сигналов и соответствующая аппаратура достаточно просты. Однако из-за несоответствия априорных характеристик сигнала характеристикам обрабатываемой реализации возможна значительная избыточность отсчетов.

Дискретизацию будем называть неравномерной, если длительность интервалов между отсчетами различна.

Выделяют две группы неравномерных методов: адаптивные и программируемые.

При адаптивных методах интервал изменяется в зависимости от текущего изменения параметров реализации сигнала.

Такие способы передачи информации очень перспективны, так как позволяют существенно уменьшить избыточность канала и тем самым увеличить фактическую пропускную способность. В настоящее время разработаны системы с адаптивной импульсно-кодовой модуляцией.

При программируемых методах изменение интервалов (частота опроса) производится либо оператором на основе анализа поступающей информации, либо в соответствии с заранее установленной программой работы.

2. Блочные и непрерывные коды. Равномерные и неравномерные коды. Коды с разделительным знаком и без разделительного знака.+ билет10 (2)

Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточны­ми и служат исключительно для коррекции ошибок. В нераз­делимых кодах такое разделение провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую к этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими

Билет№12.

1. Восстановление непрерывных функций по дискретам. Способы восстановления. Ошибка восстановления.

Восстановление непрерывной функции по дискретам- это знаем значение функции только в дискретн. моменты. Восстановление- это сглаживание функции.

2 способа: 1)ступенчатая аппроксимация. Формула : Xв(t)=X(tk)tْ. Достоинства- нет ожидания; 2) линейная интерполяция. Точность восстановления для лин интерполяции выше чем для ступенчатой аппроксимации, но требуется задержка времени и аппаратура более сложная.

2. Оптимальные и неоптимальные по длине коды. Пример оптимального по длине кода.

Билет №13

1. Теорема В.А. Котельникова и её реализация.

В.А. Котельниковым доказана теорема для функций с ограниченным (финитным) спектром (теорема отсчетов), которая формулируется следующим образом: если наивысшая частота в спектре функции x(t) меньше, чем f_m, то функция x(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/2F_m секунд.

В соответствии с этой теоремой сигнал x(t), ограниченный по спектру наивысшей частотой _m=2πf_m, можно представить рядом:

См гл 4 формулы, рисунки!!!

x(t) =  x(  )  =  x(nt)_n(t) . (4.9)

В этом выражении  = t обозначает интервал между двумя отсчетными точками на оси времени, а x(  ) = x(nt) – выборки функции x(t) в моменты времени t=nt.

Интерполяционный ряд вида (4.9) носит название ряда Котельникова. (В иностранной литературе этот ряд связывают с именами Найквиста и Шеннона).Пусть сигнал, описываемый непрерывной функцией времени x(t), имеет ограниченный спектр, т.е. преобразование Фурье:

S(j) =  x(t)e dt(4.10)

удовлетворяет условию S(j) = 0 при >_m.

В представлении сигнала интегралом Фурье пределы интегрирования можно ограничить значениями [–_m, _m]:

x(t) =   S(j)e d.(4.11)

Спектральную функцию (4.10) можно представить на интервале [–_m, _m] в виде ряда:

S(j) =  C_ke ,(4.12)

где коэффициенты разложения:

С_k =   S(j)e d.(4.13)

Сравнивая выражения (4.11) и (4.13), замечаем, что они совпадают с точностью до постоянного множителя t=π/_m, если принять t=-nt.

Следовательно:

С_k =  x(-nt).

Подставляя это выражение в формулу (4.12), спектральную функцию запишем в виде:

S(j) =   x(-nt)e (4.14)

Подставим это выражение (4.14) в формулу (4.11), изменив при этом знак при n с учетом, что суммирование проводится по всем отрицательным и положительным значениями n. Кроме того, учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и суммирования.

x(t) =   e d   x(-nt)e =  x(nt)  e d.(4.15)

После вычисления интеграла

 e d = 

и подстановки полученного результата в формулу (4.15) получим в окончательном виде выражение (4.9).

Это выражение показывает, что непрерывная функция x(t) с ограниченным спектром может быть точно представлена отсчетами функции x(nt), взятыми через равные интервалы:

t =  =  . (4.16)

Как видно из выражения (4.9), непрерывная функция x(t) представляется суммой произведений, один из сомножителей которых есть выборка функции, а другой – так называемая функция отсчетов:

_m(t) =  , (4.17)

график которой приведен на рис. 4.3.

Свойства функции отсчетов:

а) в точке t=nt _n(nt)=1, а в точках t=kt, где k – любое целое положительное или отрицательное число, отличное от n, _n(kt)=0.

б) спектральная плотность функции _n(t) равномерна в полосе частот <_m

и равна  =  .

Представление функции x(t) рядом Котельникова иллюстрируется рис. 4.4.

При выводе (4.9) предполагалось, что x(t) удовлетворяет условиям Дирихле. Это не дает возможности использовать полученный результат для функций, не стремящихся к нулю при t∞, или для функций, не интегрируемых на интервале (a, b).

Теорема Котельникова относится к сигналам с ограниченным спектром. Реальные сообщения имеют конечную длительность. Спектр таких сигналов не ограничен, т.е. реальные сигналы не соответствуют модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов по формуле (4.9) и неопределенностью выбора шага дискретизации (4.16) или частоты отсчетов F₀=2f_m.

Приведенные соображения свидетельствуют, что применение теоремы Котельникова к реальным сигналам вызывает определенные трудности в том случае, если теорема рассматривается как точное утверждение. Для практических условий, однако, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром.

Практически всегда можно определить наивысшую частоту спектра f_m так, чтобы «хвосты» функции времени, обусловленные отсеканием частот, превышающих f_m, содержали пренебрежимо малую долю энергии по сравнению с энергией исходного сигнала x(t). При таком допущении для сигнала длительностью T с полосой частот общее число независимых параметров [т.е. значений x(nt)], которое необходимо для полного задания сигнала, очевидно, будет:

N₀ =  = 2f_mT.(4.18) При этом выражение (4.9) принимает следующий вид (при отсчете времени от первой выборки):

x(t) =  x(nt) (4.19)

Величина N₀ представляет собой число степеней свободы сигнала x(t), так как даже при произвольном выборе значений x(nt) сумма вида (4.19) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала.

Параметр B=N₀, который широко применяется в системах передачи информации, называют базой сигнала.

Представление сигналов в виде ряда Котельникова положено в основу построения систем передачи информации с временным уплотнением. Смысл временного уплотнения состоит в том, что в интервале времени между двумя соседними отсчетами одного сигнала можно передавать отсчеты других сигналов. Формирование такого группового сигнала показано на рис. 4.5.

Рис. 4.5. Формирование группового сигнала в системе с временным уплотнением

2. Код с постоянным весом. Закон построения, основные характеристики.

Этот код является неразделимым, не систематическим, циклическим, нелинейным кодом длины n. Код имеет постоянное число единиц ℓ и нулей m в кодовых комбинациях характеризуется эквивалентным числом k_э информационных и r_э проверочных символов.

k_э + r_э = n, 2 ^kэ ≥ N. N – количество комбинаций кода. Длина кода n определяется путем подбора при использовании соотношения C^ℓ_n = n! / ℓ! (n- ℓ)! Обычно, ℓ ≈ n/2. В этом случае имеем наибольшее число сочетаний. Код имеет d=2 и применяется для обнаружения ошибки.

Корректирующая способность кода: код обнаруживает все ошибки за исключением одновременного перехода 1 в 0 и такого же количества переходов 0 в 1. В этом случае число 1 остается равным ℓ и такие ошибки не обнаруживаются. Процедура обнаружения состоит в подсчете числа единиц в кодовой комбинации. Результаты проверки характеризуются одним символом синдрома S=S_1. S₁ =0, если число единиц n_ℓ в принятой кодовой комбинации равно ℓ (n_ℓ = ℓ): n_ℓ = a₁^* + a₂^* + a₃^* ….. a_n^* = ℓ , то считается что ошибки нет или ошибка есть, но она не обнаруживается. Здесь осуществляется обычно сложение (не по модулю два). a₁^*, a₂^* ….. a_n^* - символы искаженной кодовой комбинации. S₁ =1, если число единиц n_ℓ в принятой кодовой комбинации неравно ℓ (n_ℓ ≠ ℓ), то ошибка есть и она обнаруживается.

Относительная скорость передачи: q = lg₂N/n

Избыточность кода: q = n-ℓog₂N / ℓog₂N

Вероятность появления ошибочной комбинации на выходе устройства обнаружения ошибок при одноразовой передаче комбинации по двоичному симметричному каналу (ДСК) равна вероятности искажения от 1 до ℓ единиц и нулей одновременно. Такие искажения не обнаруживаются.

P_ош.пр= P_н.ош = C¹_ℓ p q^{ℓ -1} C¹_n-ℓ p q^n-ℓ-1 + C²_ℓ p² q^{ℓ -2} C²_n-ℓ p² q^n-ℓ-2 + …+ C ^ℓ _ℓ p ^ℓ q^ℓ₀ C^ℓ_n-ℓ p^ℓ q^{n-ℓ- ℓ}

Последнее слагаемое приемлемо для случая ℓ ≤ n-ℓ. Если ℓ > n-ℓ, то последнее слагаемое имеет вид: C _ℓ ^{n- ℓ} p ^{n- ℓ} q^{2ℓ -n} ·C ^{n- ℓ} _{n- ℓ} p^n-ℓq⁰

Вероятность обнаружения ошибок равна:

P_{о ош.}= P_ош - P_н.ош, где P_ош = C_n¹ p¹ q^{n -1} + C_n² p² q^{n -2} + C_n³ p³ q^{n -3} + ….. C_n⁴ pⁿ q⁰ = 1-qⁿ

– вероятность искажения кодовой комбинации при всех возможных искажениях от однократных до n-кратных.

qⁿ - вероятность правильного приема кодовой комбинации длины n, q=1-p, вероятность правильного приема одного символа, p – вероятность искажения одного символа.

Пример построения кода с постоянным весом при N=0. Определим число разрядов кода n. Длина кода определяется путем подбора использованием выражения N=C^ℓ_n , где ℓ ≈n/2

Принимаем n=4, ℓ = 4/2=2. C^ℓ_n = C²₄ = 4! / 2! 2 ! = 4∙3∙2∙1/2∙1∙2∙1= 6

C^ℓ_n = C²₄ < N = 10. Число n = 4 брать нельзя;

Принимаем n=5, ℓ ≈n/2≈ 5/2 ℓ =2

C^ℓ_n = C²₅ = 5! / 2! (5-2) ! = 5∙4∙3∙2∙1/2∙1∙3∙2∙1= 10

Условие выполнено. Корректирующий код пятиразрядный с числом единиц в каждой комбинации ℓ =2 представлен в таблице. См Лабы!

Характеристики кода

1. Код неразделимый

2. Длина кода n=5. Число единиц в кодовых комбинациях ℓ =2, число 0 – n- ℓ =3

3. Кодовое расстояние d=2

4. Код обнаруживает все ошибки за исключением одновременного искажения одной любой единицы и одного любого нуля, двух единиц и двух любых нулей. Например, для комбинации 01100 одновременное искажение второго символа(10) и искажения четвертого символа (0-1). Одновременное искажение второго и третьего символа (10, 10) и четвертого и пятого импульса (01, 01)

5. Процедуру обнаружения и формирования синдрома ошибки рассмотрим на следующих примерах:

   1. передавалась комбинация 01100. В процессе передачи исказился первый символ. Вектор ошибки e = 10000. Принята комбинация 11100 n_ℓ= 1+1+1+0+0=3≠ℓ . Число единиц в комбинации n_ℓ ≠ ℓ ≠ 2. Синдром ошибки S=S₁=1. Ошибка есть и она обнаруживается

   2. передавалась комбинация 01100. В процессе передачи исказился первый и третий символ. Вектор ошибки е = 10100. Принята комбинация 11000. Число единиц в комбинации n_ℓ= 1+1+0+0+0=2=ℓ. Синдром ошибки S=S₁=0. Ошибка имеет место, но она не обнаруживается.

6. Относительная скорость передачи q= ℓog₂N / n = ℓog₂10 / 5

7. Избыточность кода И = n- ℓog₂N / ℓog₂N = 5-ℓog₂10 / ℓog₂10

8. Вероятность появления ошибочной комбинации на выходе приемного устройства равна вероятности необнаруживаемой ошибки

Р_но = С₂¹р¹q^2-1 C₃¹p¹q^3-1 + C₂²p²q^2-2 C₃²p²q^3-2 = Примем p=10^-3, тогда q=1-p = 1-10^-3 = 0,999

Р_но =2∙10^-30,999∙3∙10^-3(0,999)²+1∙(10^-3)²∙(0,999)⁰∙3∙(10^-3)²0,999=6∙10^-6∙0,997+3∙10^-12∙0,999=5,982∙10^-6+2,997∙10^-12=5,982∙10^-6

Вероятность отсутствия ошибки равна qⁿ = 0,999⁵ = 0,995

Вероятность искажения символов от однократных до пятикратных

P_1-6 = C₅¹p¹q⁴+C₅²p²q³+C₅³p³q²+C₅⁴p⁴q+C₅⁵p⁵q⁰ = 0,005

Билет №14.

1. Устройство передачи информации с обратной связью: с информационной ОС, с переносом, с командной ОС.

Нередко встречаются случаи, когда информация может передаваться не только от одного абонента к другому, но и в обратном направлении. В таких условиях появляется возможность использовать обратный поток информации для существенного повышения верности сообщений, переданных в прямом направлении. При этом не исключено, что по обоим каналам (прямому и обратному) в основном непосредственно передаются сообщения в двух направлениях ("дуплексная связь") и только часть пропускной способности каждого из каналов используют для передачи дополнительных данных, предназначенных для повышения верности.

Возможны различные способы использования системы с обратной связью в дискретном канале. Обычно их подразделяют на два типа: системы с информационной обратной связью и системы с управляющей обратной связью.

Системами с информационной обратной связью (ИОС) называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения:

1)повторить ошибочно принятые отрезки сообщения;

2)изменить применяемый код (передав предварительно соответствующий условный сигнал и убедившись в том, что он принят);

3)прекратить передачу при плохом состоянии канала до его улучшения.

В системах с управляющей обратной связью (УОС) приемное устройство на основании анализа принятого сигнала само принимает решение о необходимости повторения, изменения способа передачи, временного перерыва связи и передает об этом указание передающему устройству. Возможны и смешанные методы использования обратной связи, когда в некоторых случаях решение принимается на приемном устройстве, а в других случаях на передающем устройстве на основании полученной по обратному каналу информации.

Наиболее распространены системы с УОС при использовании одновременно с обнаружением ошибок. Такие системы часто называют системами с переспросом, или с автоматическим запросом ошибок

2.Основные понятия модуляции: переносчик, модулирующие воздействия, сигнал. Одновременная модуляция переносчика по нескольким параметрам. Типы модуляции.

Преобразование дискретного сообщения в сигнал состоит из двух операций: кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция – вид формируемого сигнала, который должен передаваться по каналу связи.

Передача сообщений по каналу связи осуществляется с помощью некоторого физического процесса, который называется переносчиком. В системах передачи информации переносчиком является электрическое колебание. Всякий сигнал получается путем модуляции.

Общий принцип модуляции состоит в изменении одного или нескольких параметров несущего колебания (переносчика) f(а,b,...,t) в соответствии с передаваемым сообщением.

Так, например, если в качестве переносчика выбрано гармоническое колебание , то можно образовать три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ). Если переносчиком является периодическая последовательность импульсов, то при заданной форме импульсов можно образовать четыре основных вида импульсной модуляции: амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), время- импульсную (ВИМ, ФИМ) и частотно-импульсную (ЧИМ).

Билет№15.

1. Физические характеристики сигнала, помехи и канала. Объём сигнала и ёмкость канала. Согласование объёма сигнала с ёмкостью канала.

В качестве сигнала можно использовать любой физический процесс, изменяющийся в соответствии с передаваемым сообщением. Существенно то, что сигналом является не сам физический процесс, а изменение отдельных параметров этого процесса. Сигналы являются материальными носителями информации.

Сигнал характеризуется 3 св- ми:

:1)длительность (время сущ. сигнала, Т[ сек], дин. диапазон сигнала должен быть выше чем средняя мощность помех сигнала Д=10 lg Pc max/Pc min (дБ) );

2)превышение Н=logPc/Pп;

3)полоса частот( ширина спектра сигнала Fc);

Каналом связи принято называть совокупность технических средств, служащих для передачи сообщения от источника к потребителю. Этими средствами являются передатчик, линия связи и приемник. Канал характеризуется теми же хар-ми:

1) время отводимое в канале для передачи сигнала;

2)дин.диапазон канала

3)полоса пропускания канала связи.

Тс<Tk, Hc<Hk, Fc<Fk (больше или равно).

2. Виды модуляции импульсного переносчика. Краткая характеристика основных видов дискретной импульсной модуляции.

1)амплитудно-импульсная модуляция

2)полярно-импульсная модуляция(всегда дискретна)

Билет№16.

1. Виды и характеристики сигналов при дискретной импульсной модуляции.

При дискретной (цифровой) модуляции закодированное сообщение a_i, представляющее собой последовательность кодовых символов {b_i}, преобразуется в последовательность элементов (посылок) сигнала {s_i (t)} путем воздействия кодовых символов на переносчик s (t) . Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого могут являются величина и направление тока. Обычно в качестве переносчика, как и в непрерывной модуляции, используют переменный ток (гармоническое колебание).На рис. 3.1 приведены формы сигнала при двоичном коде различных видов дискретной или цифровой модуляции (манипуляции). При АМ символу 1 соответствует передача несущего колебания в течение времени Т (посылка), символу 0 – отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой f₁ соответствует символу 1, а передача колебания с частотой f₀ соответствует 0. При двоичной ФМ меняется фаза несущей на π при каждом переходе от 1 к 0 и от 0 к 1.

Рис.3.1. Формы сигналов при двоичном коде для различных видов дискретной модуляции см глава3! На практике применяют систему относительной фазовой модуляции (ОФМ). В отличие от ФМ при ОФМ фазу сигналов отсчитывают не от некоторого эталона, а от фазы предыдущего элемента сигнала. Например, символ 0 передается отрезком синусоиды с начальной фазой предшествующего элемента сигнала, а символ 1 – таким же отрезком с начальной фазой, отличающейся от начальной фазы предшествующего элемента сигнала на π. При ОФМ передача начинается с посылки одного не несущего информации элемента, который служит опорным сигналом для сравнения фазы последующего элемента.

В более общем случае дискретную модуляцию следует рассматривать как преобразование кодовых символов 0, 1, … , т - 1 в определенные отрезки сигнала s_i(t), где i = 0, 1, … , т - 1 – передаваемый символ. При этом вид сигнала s_i (t), в принципе, может быть произволен. В действительности его выбирают так, чтобы удовлетворить требованиям, предъявляемым к системе передачи информации (в частности, по скорости передачи и по занимаемой полосе частот), и чтобы сигналы хорошо различались с учетом воздействующих помех.

Длительность посылки первичного сигнала b_n(t) при дискретной передаче определяет скорость передачи посылок (техническую скорость или скорость модуляции). Эта скорость выражается числом посылок, передаваемых за единицу времени. Измеряется техническая скорость в Бодах. Один Бод – это скорость, при которой за одну секунду передается одна посылка.

2. Корректирующие и некорректирующие коды. Код с обнаружением ошибок и коды с обнаружением и исправлением ошибок.

По помехоустойчивости коды делятся на обыкновенные (некорректирующие) и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются обыкновенными, или кодами без избыточности. В обыкновенных равномерных кодах превращение одного символа комбинации в другой, например, 1 в 0 или 0 в 1, приводит к появлению новой возможной комбинации, т.е. к ошибке. Корректирующие коды строятся так, что для передачи сообщения используются не все возможные кодовые комбинации, а лишь некоторая их часть. Тем самым создается возможность обнаружить и исправлять ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются ценой введения в кодовые комбинации дополнительных (избыточных) символов.В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если, он позволяет обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны такие коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы код обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов. Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки. Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточны­ми и служат исключительно для коррекции ошибок. В нераз­делимых кодах такое разделение провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.В свою очередь, линейные коды могут быть разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую к этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими

Билет№17.

1. Понятие передачи информации. Простейшая система передачи информации. Основные определения и характеристики.

Объектом передачи служит сообщение. Оно содержит всю передаваемую и вспомогательную инф, необходимую для передечи. Мерой количества информации в сообщениях должна служить величина, измеряющая изменение вероятности события под действием сообщения. Любое сообщение может быть непрерывным (речь, музыка) или дискретным (письменный текст, цифровые данные).

Функциональная схема системы передачи информации (СПИ)

Источником информации является отправитель сообщения, а потребителем – ее получатель. Поступающее от источника сообщение u(t) в передатчике обрабатывается опр. образом, и формируется сигнал s(t), удобный для передачи по линии связи. Сигнал распространяется по линии связи.

Линией связи называется среда, используемая для передачи сигналов от передатчика к приемнику. В системах электрической связи – это пара проводов, кабель или волновод; При передаче сигнал может искажаться, т.к. на него могут воздействовать помехи w(t). Приемник обрабатывает принятый сигнал x(t), искаженный помехой, и восстанавливает по нему переданное сообщение u(t). Помехи имеют ту же природу, что и сигнал. Появляются из космоса, атмосферы(гроза), пром-ти.

Каналом связи принято называть совокупность технических средств, служащих для передачи сообщения от источника к потребителю. Этими средствами являются передатчик, линия связи и приемник. Канал связи вместе с источником и потребителем образуют систему передачи и обработки информации.

Различают системы передачи дискретных сообщений (например, система телеграфной связи, система передачи цифровых данных) и системы передачи непрерывных сообщений (системы радиовещания, телевидения и т.д.). Система передачи информации называется многоканальной, если она обеспечивает взаимонезависимую передачу нескольких сообщений по одному каналу связи.

2. Понятие переносчика информации. Типы переносчиков. Модуляция и демодуляция.

Переносчик - физ.процесс,способный распространяться по линии связи от передатчика к приёмнику. Переносчик хар-ся 3 параметрами: амплитуда, фаза, и частота. В устройствах передачи, в которых информация от передатчика к приёмнику доставляется при помощи электрических сигналов, переносчиком является электрический ток или электромагнитная волна. Два наиболее часто используемых в телемеханике типа электрических переносчиков – постоянный ток и гармонический ток.

Для того, чтобы передать сообщение нужно его нанести на переносчик, т.е. осуществить модуляцию. Модуляция осуществляется с помощью изменения параметров переносчика. Демодуляция(детектирование)-операция обратная модуляции-это извлечение сообщения из модулированного сигнала(или это Процесс восстановления воздействия, которое было оказано на переносчик при модуляции, по значениям одного или нескольких параметров сигнала). В системах передачи непрерывных сообщений в результате демодуляции выделяется видеосигнал, отображающий переданное сообщение. В системах передачи дискретных сообщений в результате демодуляции последовательность элементов сигнала превращается в последовательность кодовых символов. Декодирование- это процесс, когда последовательность кодовых символов преобразовывается в последовательность элементов сообщения.

. Билет №18.

1. Виды каналов связи, применяемых для передачи информации(См Билет № 24(1)). Способы разделения каналов.Искажение сигналов в каналах связи.

Искажение сигналов в каналах связи.

Передача сигналов по реальным каналам всегда сопровождается изменениями (преобразованиями) этих сигналов. Обратимые преобразования не влекут за собой потери информации. При необратимых преобразованиях потери информации неизбежны. Поэтому для обратимых преобразований сигнала называют «искажение», а необратимые преобразования - «помехами».

Искажения: а) линейные появляются в лин. инерционном 4хполюснике с постоянными параметрами из-за наличия в нем реактивных элементов. При линейных искажениях нарушаются существующие частотные и фазовые соотношения между отдельными составляющими сигнала и форма сигналов. б) нелинейными возникают в нелин. безынерционных 4хполюсниках с постоянными параметрами из-за нелинейности характеристик активных элементов: транзисторов, диодов и др. В результате нелинейных искажений спектр сигналов расширяется, в них появляются дополнительные компоненты, растут уровни взаимных помех в каналах.

Способы разделения каналов:

1)частотный (см билет 28(1))

2)временной (см билет №29(1))

3)комбинационный Разделение сигналов b_r, основанное на различии в комбинациях сигналов разных каналов, называется комбинационным.

Здесь первичные сообщения b₁(t),b₂(t),... b_N(t), от N источников поступают на вход кодера, выполняющего функции устройства объединения каналов (УОК). Полученное групповое сообщение b_r(t) преобразуется с помощью группового модулятора М в групповой сигнал u_r(t), поступающий в групповой тракт. На приемной стороне после демодуляции и декодирования формируются канальные сообщения, соответствующие N первичным сообщениям. Типичным примером комбинационного уплотнения является система двукратной частотной модуляции (ДЧМ).

2. Основные характеристики корректирующих кодов (разрядность, число информационных сигналов, избыточность, кодовое расстояние, корректирующая способность, оптимальность).

Код называется корректирующим, если, он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи.

Для того чтобы код обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Кодовое расстояние - это это минимальное значение из всех кодовых расстоянии. Если код корректирующий => кодовое расстояние>1.

Корректирующая способность кода – это способность кода обнаружить или обнаружить и исправить ошибки.

Коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточны­ми и служат исключительно для коррекции ошибок. В нераз­делимых кодах такое разделение провести невозможно.

Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений. Статистическим, или оптималь­ным, называется кодирование, при котором наилучшим об­разом используется пропускная способность канала без по­мех. При оптимальном кодировании фактическая скорость пе­редачи информации по каналу R приближается к пропуск­ной способности С, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответство­вали ограничениям, которые накладываются на сигналы, пе­редаваемые по каналу связи. Поэтому структура оптималь­ного кода зависит как от статистических характеристик ис­точника, так и от особенностей канала.

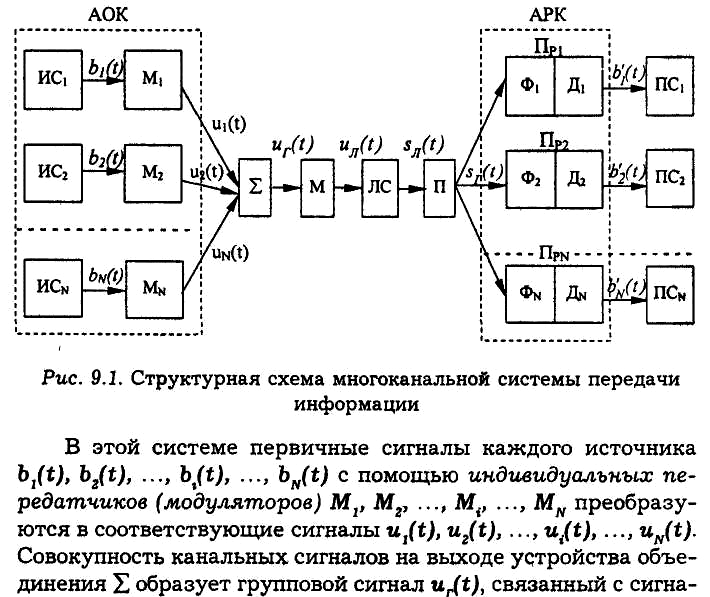
Билет№19.

1. Многоканальная система передачи информации.

Многоканальными наз. системы передачи, обеспечивающие передачу большого числа сообщений различных источников ин­формации по общей линии связи. Многоканаль­ные системы могут быть анало­говыми и цифровыми.

u_л(t)- линейный сигнал

s_л(t)- принимаемый линейный сигнал

u_Г(t)- групповой сигнал

s_i(t)- канальные сигналы, которые посредством детектирования преобразуются в предназначенные индивидуальным получателям сигналы: b^|₁(t), b^|₂(t), …., b^|_i(t), ……, b^|_N(t).

Канальные передатчики вместе с устройствами объединения образуют аппаратуру объединения (уплотнения) каналов АОК.

Группой передатчик(М), линия связи (ЛС) и групповой приемник (Пр) составляют групповой тракт передачи, который вместе с аппаратурой объединения и разделения каналов составляет систему многоканальной связи. Аппаратуру индивидуальных приемников, обеспечивающую выделение сигналов s_i(t) из группового сигнала с допустимыми искажениями, называют аппаратурой разделения каналов (АРК).

Чтобы разделяющие устройства были в состоянии различать сигналы отдельных каналов, должны существовать определенные признаки: параметры переносчика (амплитуда, частота или фаза, временное положение, длительность или форма сигнала).

2. Идея исправления ошибок корректирующим кодом(см билет №21(2)). Принцип разбиения запрещённых комбинаций на подмножества.

Билет№20.

1. Математические характеристики каналов связи.

Канал передачи информации предназначен для передачи сообщения от источника к потребителю.

Пропускная способность канала С=V_максH, где V – скорость передачи электрических кодовых сигналов, Н – энтропия сообщения.

Коэффициент использования канала η=V/C, 0 ≤ η ≤1, так как 0 ≤ V ≤С

Для идеального дискретного канала

Кодер обеспечивает преобразование передаваемых сигналов в электрические кодовые сигналы. В идеальном канале между элементами кодовых сигналов на входе и выходе существуют однозначное соответствие. Скорость передачи информации равна производительности кодера Ck=VkHk [бит/с]

Пропускная способность идеального канала

C=Vmax=V_klogm_k, где m_k – основание кода. Пропускная способность является предельной характеристикой канала.

Максимальное количество информации в одной кодовой комбинации Hmax=nlogm_k

Пропускная способность

Таким образом пропускная способность идеального дискретного канала полностью определяет скорость передачи сигналов и основание кода.

2. Код с проверкой на четность: процедуры построения и основные характеристики.

Этот код является простейшим разделимым систематическим циклическим линейным кодом длины n с k = n-1 информационными и r = 1 проверочным символом. Обозначается как (n, n-1)-код. Его комбинации обладают свойством цикличности, поэтому код является циклическим.

В рамках ТЛ3 проверочный символ находится как сумма по модулю два всех информационных символов !111

При таком способе нахождения b₁ число единиц в любой кодовой комбинации кода четно. Код имеет d = 2 и применяется для обнаружения ошибки.

Корректирующая способность кода: код обнаруживает ошибки любой нечетной кратности в пределах n.

Процедура обнаружения состоит в проверке на четность всей принятой комбинации. Результат этой проверки характеризуется одним символом синдрома S: S = S₁

!!!

где a_i*, b_i* - значения информационных и проверочных символов в принятой кодовой комбинации.

Считается, что если S₁ = 0, то комбинация принята без ошибок (ошибки нет или есть ошибки четной кратности), если S₁ =1, то комбинация принята с ошибками.

Относительная скорость передачи q = k/n .

Избыточность кода И = 1/k.

Вероятность появления ошибочной комбинации на выходе устройства обнаружения ошибок при одноразовой передаче комбинации по двоичному симметричному каналу (ДСК) равно вероятности появления ошибок четной кратности:

Вероятность обнаружения ошибок равно вероятности появления ошибок нечетной кратности:

Пример построения кода с проверкой на четность при N = 8, k = 3 (2³ = 8) и r = 1.

Процедура построения: Строится первичный (обычный двоичный) код длины k=3, затем с правой стороны приписывается 1 или 0 по правилам, изложенным выше. Построение кода с проверкой на четность отражено в таблице.!1!1

Характеристики кода

11. Код разделимый

12. Число информационных символов k=3

13. Число проверочных символов r=1

14. Длина кода n = k+r = 3+1= 4

15. Кодовое расстояние d=2

16. Корректирующая способность кода – код обнаруживает однократные и трехкратные ошибки

17. Процедуру обнаружения и формирования синдрома ошибки рассмотрим на следующих примерах:

    1. передавалась комбинация 0110, принята комбинация 1110 (искажен первый символ). Синдром ошибки S₁ =1 Å 1 Å 1 Å 0 = 1, S = 1 – ошибка есть и обнаружена

    2. передавалась комбинация 0110, принята комбинация 1010, искажены первый и второй символы. Синдром ошибки S₁ =1 Å 0 Å 1 Å 0 = 0, S = 0 – ошибка есть, но она не обнаружена

18. Относительная скорость передачи q = k/n = ¾

19. Избыточность кода И = 1/k = 1/3

20. Вероятность появления ошибочной комбинации на выходе устройства обнаружения при вероятности перехода 1 в 0 и 0 в 1. р=10^-5 и вероятности приема неискаженных символов q=1-p=1-10^-5 равна:

Р_ош = С²_n p² q^n-2 + C⁴_n p⁴ q^n-4 = С²₄ p² q^4-2 + C⁴₄ p⁴ q^4-4 = 6∙(10^-5)²∙(1-10^-5)² +

1∙ (10^-5)⁴(1-10^-5)⁰ ≈ 6∙10^-10

Вероятность необнаружения однократных и трехкратных ошибок:

Р_но = С¹_n p¹ q^n-1 + C³_n p³ q^n-3 = 4∙p q^4-1 +4∙p³ q^4-1 = 4∙10^-5 (1-10^-5)³ + 4∙ (10^-5)³∙ (1-10^-5)⁰ 4∙10^-5

Билет№21.

1. Случайные сигналы и их аналитическое описание. Одномерный закон распределения мгновенных значений случайной функции.

2. Идея обнаружения ошибок корректирующим кодом

Корректирующие коды строятся так, что для передачи сообщения используются не все кодовые комбинации mⁿ, а лишь некоторая часть их (так называемые разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации дополнительных (избыточных) символов

Возможность обнаружения ошибочных символов в комбинациях равномерного блокового кода с основанием m и длиной n основана на том, что в него входят не все N₀ = mⁿ кодовых комбинации нормального кода, а только часть из них. Другими словами, число входящих в корректирующий код комбинаций

N < N₀

Используемые в корректирующем коде комбинации называются разреженными, а остальные комбинации нормального кода, число которых N₀ – N , — непрерывными.

Если принятая комбинация является запрещенной, то это говорит о том, что при передаче разрешенной комбинации в ней появились ошибочные символы. Естественно, что в ряде случаев ошибки могут перевести одну разрешенную комбинацию в другую. В этом случае ошибки не обнаруживаются.

Ошибки обнаруживаются всякий раз, когда любая разрешенная комбинация переходят в любую запрещенную. Число таких случаев N(N₀ – N). Ошибки не обнаруживаются, если разрешенная комбинация переходит в любую другую разрешенную. Число таких случаев N(N – 1). Общее число случаев перехода комбинаций в результате искажений в разрешенные и запрещенные для кода в целом N(N₀ – 1).

Билет №22.

1. Многомерный закон распределения мгновенных значений случайных функций.

2. Понятие системного линейного и циклического кода.

Систематические коды относятся к блочным раздели­мым кодам, т. е. к кодам, где операция кодирования осуще­ствляется независимо в пределах каждой комбинации, состо­ящей из информационных и контрольных символов.

Кодирующие и декодирующие устройства цикличес­ких кодов в большинстве случаев обладают сравнитель­ной простотой, что следует считать одним из основ­ных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где дей­ствуют импульсные и сосредоточенные помехи или на­блюдаются замирания сигналов.

Билет №23.

1. Гауссовский случайный процесс, белый шум.

Имеет распределение Гаусса или норм.распределение.

При Σ достат. большого числа независимых или слабо завис. величин распределение Σ близко к нормальному при любом распределении отдельных слагаемых. P(x) позв. находить относит. время пребывания сигнала x(t) в определенном интервале времени. Пик-фактор это отношение максимального значения к среднеквадратическому.

2. Коды, построенные с использованием многочлена, порождающий многочлен, порождающая матрица.

Построение кодов. (Всего пять кодов)

(n,k) – коды: g₁ = x+1, (7,6) код,

g₂ = x³ + x + 1, (7,4) код,

g₃ = x³ + x² + 1, (7,4) код,

g₄ = x⁴ +x³ + x² + 1, (7,3) код,

g ₅= x⁴ + x² + x + 1, (7,3) код.

Используются схемы деления и схемы сложения информационной части кода и остатка A(x) + R(x)

Для каждого из пяти кодов предусматривается возможность построения всех комбинаций кода. 2^к – комбинаций. Первый код – 64 комбинации, второй и третий код – 16 комбинаций, 4 и 5 код – 8 комбинаций.

Пример. Порожд. многочлен: g₂ = x³ + x + 1, (7,4) – код, к = 4, N = 16, двучлен : x⁷ + 1,

h(x)= x⁷ + 1/ x³ + x + 1= x⁴ + x² +x + 1. Ну=

Обнаружение: нах.синдром ошибки и по его виду решается есть ошибка или нет; 2) если мы разделим комбинацию на порожд. многочлен g(x) мы получим остаток равный 0 или не равный 0. x⁶ + x⁵ + x⁴ + x³ + 1/ x³ + x + 1= x³ + x² + 1, остаток равен x² + x. Это значит что синдром равен 110.

Билет№24.

1. Каналы передачи информации, общие сведения. Классификация каналов передачи.

Канал связи - совокупность средств (техн.устройства и линия связи), предназначенных для передачи сигналов (сообщений) между различными точками системы передачи информации (информационной системы). Канал связи можно представить как последовательное соединение устройств (блоков), выполняющих различные функции в общей системе передачи информации.

По характеру сигналов на входе и выходе каналы делятся на:

а) непрерывные (по уровням), на входе и выходе которых сигнал непрерывен. Пример: канал, заданный между выходом модулятора и входом демодулятора в системе передачи информации;

б) дискретные (по уровням), на входе и выходе которых сигналы дискретны. Пример: канал, заданный от входа кодера до выхода декодера;

в) дискретные со стороны входа и непрерывные со стороны выхода или наоборот. Такие каналы называются дискретно-непрерывными, или полунепрерывными (например, каналы, заданные между входом модулятора и входом демодулятора или между выходом модулятора и выходом декодера).

Также каналы делятся на:

- временные (с сосредоточенными параметрами), в которых сигналы на входе и выходе описываются функциями одного скалярного параметра (времени), и пространственно-временные каналы (с распределенными параметрами), в которых сигналы на входе и (или) выходе описываются функциями более одного скалярного параметра.

- по диапазону рабочих частот: до неск.сотен кГц (на современных симметричных кабельных линиях связи), до сотни МГц (коаксиальные кабели), не выше 150 кГц (на воздушных проводных линиях).

- по хар-ру на входе и выходе каналы связи делятся на: непрерывные по уровню и дискретные по уровню.

- по ширине полосы пропускания: телеграфные(тоналтный диапозон) 240Гц; телефонные (стандарт) 300-3400 Гц; широкополосные (стандарт) 60,6-107,4кГц ~ 47кГц.

- по количеству линий связи: донородные (1) и составные(неск).

2. Сообщения и сигналы, формы их представления и виды преобразования

Билет№25.

1. Анализ непрерывных каналов передачи информации.

Основными задачами анализа непрерывных каналов являются анализ линейных и нелинейных искажений сигналов в каналах и анализ влияния помех в каналах.

Для анализа искажений сигналов в каналах необходимо располагать сведениями о характеристиках входных сигналов, структуре и параметрах операторов преобразования сигналов. Входные сигналы определяются типом модуляции

При строгом рассмотрении реальные непрерывные каналы являются нелинейными инерционными системами со случайными параметрами (стохастические системы). В них реакция на выходе не может предшествовать воздействию на входе, поэтому такие системы часто называют динамическими.

Передача сигналов по реальным каналам всегда сопровождается изменениями (преобразованиями) этих сигналов. Обратимые преобразования не влекут за собой потери информации. При необратимых преобразованиях потери информации неизбежны. Поэтому для обратимых преобразований сигнала также часто используется термин «искажение», а необратимые преобразования называют «помехами».

Линейные искажения сигналов появляются в линейном инерционном четырехполюснике с постоянными параметрами из-за наличия в нем реактивных элементов. Нелинейными называются искажения сигналов, которые возникают в нелинейных безынерционных четырехполюсниках с постоянными параметрами из-за нелинейности характеристик активных элементов: транзисторов, диодов и др. Выходной сигнал представляют в виде:

x(t, ) = μ(t)S[t – (t)] + (t), (5.1)

где S(t) – входной сигнал; μ(t) и (t) – соответственно мультипликативная и аддитивная помехи; (t) – задержка сигнала в канале.

Мультипликативные помехи обусловлены случайными изменениями коэффициента передачи канала из-за изменения характеристик среды, в которой распространяются сигналы. Аддитивные помехи обусловлены флуктуационными явлениями (случайными колебаниями тока и напряжения), связанными с тепловыми процессами в проводах, резисторах, транзисторах и других элементах схем, наводками под действием атмосферных явлений (грозовые разряды и т.д.) и индустриальных процессов (работа промышленных установок, других линий связи и т.д.).

Аддитивные помехи делят на сосредоточенные и флуктуационные. Сосредоточенные аддитивные помехи отличаются сосредоточенностью энергии помех в полосе частот (узкополосные помехи) или на отрезке времени (импульсные помехи).

Флуктуационная аддитивная помеха характеризуется «размытостью» энергии спектра в широком диапазоне частот. Она обусловлена главным образом внутренними шумами элементов аппаратуры (тепловой шум, дробовой эффект и т.д.). Средняя мощность теплового шума в полосе частот F полезного сигнала определяется по формуле:

P = ² = 4kT⁰F

Математическими моделями сосредоточенных аддитивных помех являются узкополосные случайные сигналы и случайные последовательности импульсов. Математической моделью флуктуационной аддитивной помехи служит гауссовский «белый шум».

Идеальный канал можно применять как модель реального непрерывного канала, если соблюдаются следующие условия: помехи любого вида отсутствуют, преобразование сигналов в канале является детерминированным, мощность и полоса сигналов ограничены. Модель идеального канала слабо отражает реальные условия, ее применяют чаще всего для анализа линейных и нелинейных искажений модулированных сигналов в многоканальных системах проводной связи.

Гауссовский канал применяются на каналах проводной связи и однолучевой радиоканал. В этом канале время задержки не зависит от текущего времени, присутствует аддитивная помеха в виде Гауссовского «белого шума».

Гауссовский канал с неопределенной фазой сигнала. В этой модели время задержки сигнала в канале рассматривают как случайную величину, поэтому фаза выходного сигнала также случайна.

Гауссовский однолучевой канал с замираниями.Спектр вых сигнала шире входного. Применяется для радиоканалов различных диапазонов и проводных каналов со случайными параметрами.

Гауссовский многолучевой канал с замираниями. Эта модель описывает радиоканалы, распространение сигналов от передатчика к приемнику происходит по различным «каналам» – путям. Самая сложная модель.

Основной метод борьбы с помехами – улучшение физ. характеристик систем.

Основные задачи анализа непрерывных каналов: анализ влияния помех на сигналы и анализ линейных и нелинейных искажений.

2. Представление кода многочленами. Операции с многочленами.

Билет№26.

1. Анализ дискретных каналов передачи информации.

Дискретный канал образуют устройства тракта «вход кодера – выход декодера»(см билет 24(1) рисунок. На вход канала поступают символы a_k1, а с выхода – a_k2. Математическая модель дискретного канала определена, если известны следующие характеристики: алфавит и априорные вероятности P(a_k1) появления символов a_k1 сообщений (k=1, …, m₁, m₁ – объем алфавита); скорость передачи символов W₁; алфавит символов a_i2 сообщений (i=1, …, m₂, m₂ – объем алфавита); априорная условная вероятность P(a_i2/a_k1) появления символа a_i2 при условии, что был передан a_k1.

Первые две характеристики определяются свойствами источника сообщений и полосой пропускания непрерывного канала.

Объем выходного алфавита m₂ определяется способом построения системы передачи информации. Условная вероятность P(a_i2/a_k1) определяется в основном свойствами непрерывного канала и его характеристиками. Если в системе используется канал обратной связи и «стирание» символов, то m₂>m₁. Стирание символов вводят тогда, когда из-за искажений и помех неясно, какой символ передавался. Решающее устройство декодера выдает символ стирания, если символ a_i2 настолько отличается от символов источника сообщений, что его нельзя с большой вероятностью отождествить ни с одним из передаваемых. Стирание символов позволяет уменьшить вероятность появления ошибки, но приводит к уменьшению вероятности правильного приема. Определены условия, при которых стирание символов целесообразно. Обычно вводят один символ стирания.

Результатом анализа дискретного канала является определение апостериорной условной вероятности Р(а_к1 /a_i2) того, что при получении символа a_i2 передавался символ a_i2.

С помощью этих апостериорных вероятностей и априор­ных вероятностей Р(а_к1) рассчитывают полную вероятность появления ошибки в канале, полную вероятность правильного приема, вероятность появления символов на выходе канала, информационные характеристики дискретного канала (скорость передачи информации, пропускную способность, количество принятой информации и др.).

Если решающая схема декодера реализует алгоритм определения максимума апостериорной вероятности:

Апостериорная вероятность рассчитывается по формуле Байеса:

то на выходе декодера появится символ a_j1 апостериорная вероятность появления которого Р(а_j1 /a_i2) больше всех остальных. Характер условных вероятностей Р(а_i21 /a_k1) полностью определяет свойства дискретного канала. Если для любых соче­таний а_i2 и а_к1 эта вероятность не зависит от момента времени t взятия отсчета, т. е.:

то канал называют однородным. Если условия (5.7) не вы­полняются, то канал называется неоднородным. Если справедливо условие:

то канал называют каналом без памяти. Реальные дискретные каналы являются неоднородными и с памятью. Это обусловлено следующими причинами: искажением сигналов и влиянием помех в непрерывном канале, задержкой во времени выходной последовательности сиг­нала по отношению к входной, нарушением тактовой синхронизации передаваемых и принимаемых импульсов, ошибками решающих схем. Однако модель дискретного однородного канала без памяти как модель первого приближения находит широкое применение. Она позволяет упростить методы анализа и получения исходных данных.

2. Обнаружение, исправление ошибки с использованием многочленов, синдром ошибки и методы его определения.

Билет№27.

1. Принципы многоканальной передачи информации.

Канал- это совокупность тех.средств и линий связи. Линии связи-самый дорогой Эл-т в системе. Каналы связи характеризуются пропускной способностью- измер. количеством инф. в единицу времени., С*= бит/сек.

R ик- производительность к-го источника информации. С*>=Σ R ик.

Многоканальная сист.как и одноканальная может быть аналоговой и цифровой. Аналоговые многоканальные системы- в них имеется осн.стандарт канал(300-3400 Гц. Аналоговые объединены в группы. Цифровые- скорость 64 кбит/сек. Они формируются по иерархич. принципу.

Осн.свойство: необходимо исп.признаки пригодные только для данного канала.

Разделение канала бывает по: времени,частоте и по форме.

2. Системы счисления и кодирования

Билет№28.

1. Частотное разделение каналов передачи информации.

В многоканальных системах с частотным разделением каналов эффективно используется лишь около 80% полосы пропускания тракта передачи. Кроме того, необходимо обеспечить очень высокую степень линейности всего тракта группового сигнала. Для снижения взаимных переходных помех между каналами до допустимого уровня приходится вводить защитные частотные интервалы ∆ f_защ

2. Определение и классификация сигналов. Непериодические сигналы. Детерминированные, случайные процессы.

Передача и хранение информации, т.е. перенос информации в пространстве и времени, осуществляется сигналами.

Сигналами называются физические процессы, параметры которых содержат информацию, т.е. сигналы являются материальными носителями информации. В исходном состоянии носитель информации представляет собой как бы чистую поверхность, подготовленную к нанесению необходимых данных – модуляции. Сигналы можно классифицировать по ряду признаков. различают дискретные и непрерывные сигналы, которые, в свою очередь могут быть детерминированными или случайными. Дискретный сигнал представляет собой дискретную последовательность определенных элементов, соответствующую элементам передаваемого сообщения. Непрерывный сигнал может принимать любые значения в заданном интервале времени.

Сигнал называется детерминированным или регулярным, если его математическим представлением является заданная функция времени.

В реальных системах передачи всегда действуют непериодические сигналы, так как все сигналы имеют конечную длительность.

при гармоническом анализе непериодической функции получается сплошной спектр, состоящего из бесконечно большого количества гармоник с бесконечно малыми амплитудами.

Билет№29.

1. Временное разделение каналов передачи информации.

При временном разделении существует взаимные помехи. Они опр-ся тем,что спектр ограничен и АЧХ ФЧХ неидеальны. Для снижения уровня взаимных помех нужно вводить «защитные» временные интервалы.

Системы с временным разделением каналов находят широкое применение при передаче непрерывных сообщений с помо­щью аналоговых видов импульсной модуляции (ФИМ, ШИМ), но особенно в цифровых системах с ИКМ .

2. Амплитудная модуляция

Билет№30.

1. Общие сведения о приеме сигналов. Методы накопления.(глава8)

2. Угловая модуляция.

При изменении частоты всегда меняется фаза колебаний, а при изменении фазы меняется частота. Этим определяется общий характер частотной (ЧМ) и фазовой (ФМ) модуляции. Поэтому их часто объединяют под общим названием угловой модуляции. Для простого гармонического колебания:

s (t) =А₀ cos( ω₀ t + ₀ ) = А₀cos ψ (t)

набег фазы (изменение фазы) за какой-либо конечный промежуток времени от t = t₁ до t = t₂ равен:

ψ(t₂) - ψ(t₁) = (ω₀ t₂ + ₀ ) - (ω₀ t₁ + ₀ )= ω₀ (t₂ - t₁)

Угловую частоту можно определить как отношение:

(t₂) - (t₁)

₀ =  .

t₂ – t₁

Отсюда видно, что угловая частота есть не что иное, как скорость изменения фазы колебания. Где (t₂) -фаза колебания, t_{2 и} t₁ - моменты времени. В случае сложного колебания, частота которого меняется во времени:

∞ ψ(t₂) - ψ(t₁) =  ω(t) dt; зав-ть между частотой и фазой:

-∞

ω(t) =2 π f(t) – мгновенная угловая частота колебания; f(t) – мгновенная частота.

Полную фазу колебания можно представить в виде:

ψ(t) =ω₀(t) + (t) +₀ . (3.11)

Общее выражение для высокочастотного колебания, амплитуда которого постоянна(А (t) =А₀), а аргумент ψ(t) модулирован, записывается в след. форме:

s (t) =А₀ cos [ω₀ t + (t) + ₀]. (3.12)

Простейшая гармоническая ЧМ, когда мгновенная частота колебания определяется выражением:

ω(t) = ω₀ +ω₀ cos Ωt, (3.13)

где ω₀ =2 π f₀ представляет собой амплитуду частотного отклонения. Для краткости ₀ в дальнейшем будем называть девиацией. Через ω₀ и Ω обозначены несущая и модулирующая частоты.

Таким образом подставляя формулу 3.13 в 3.11 и 3.12 получим

₀

s (t) =А₀ cos [ω₀ t +  sin Ωt + ₀] . (3.15)

Ω

Фаза колебания s (t) наряду с линейно возрастающим слагаемым ω₀t содержит

₀

еще периодическое слагаемое  sinΩt. Это позволяет рассматривать s(t) как

Ω

колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к закону изменения частоты. Именно модуляция частоты по закону _д cos Ωt приводит к модуляции фазы по закону:

_д

 sinΩt. Амплитуду изменения фазы :

Ω

_д

_maх =  = m

Ω называют индексом угловой модуляции.

Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω₀, а определяется исключительно девиацией ω_д и модулирующей частотой Ω.

Билет№31.

1. Поперечный и непоперечный прием сигналов.

2. Прием на согласованный фильтр.

Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна. К таким сигналам, в первую очередь, относятся дискретные двоичные сигналы. В этих случаях важным параметром, характеризующим качество обнаружения , явл. отношение сигнала к помехе. Линейный фильтр максимизирующий это отношение, называется оптимальным согласованным фильтром.

Амплитудно-частотная характеристика согласованного фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнала, а фазочастотная характеристика определяется фазовым спектром сигнала φ(ω) и линейной функцией частоты ωt₀. Таким образом, частотная характеристика оптимального фильтра полностью определяется спектром сигнала, "согласована" с ним. Отсюда и название — согласованный фильтр.

. Билет№32.

1. Корреляционный и автокорреляционный прием сигналов.

В зависимости от метода регистрации сигнала на выходе корреляционный прием может быть когерентным и некогерентным.

Отношение сигнала к помехе на выходе корреляционного приемника при когерентном приеме будет равно:

При некогерентном приеме это отношение будет в два раза меньше:

Корреляционный способ приема можно рассматривать как обобщение метода накопления на сигналы произвольной формы.

В схеме автокорреляционного приемника отсутствует специальный генератор опорных колебаний.

В данной схеме имеется линия задержки ЛЗ, осуществляющая задержку принимаемого сигнала на время τ. Задержанное колебание x(t - τ) используется в качестве опорного.

При большом уровне помех (qвx<<1) автокорреляцион­ный приемник по помехоустойчивости приближается к приемнику с квадратичным детектором. Более низкая помехоустойчивость автокорреляционного приемника по сравнению с корреляционным при любых значениях q_вx обусловлена наличием помехи в тракте опорного напряжения. Автокорреляционный прием возможен и в том случае, когда отсутствуют сведения не только о фазе сигнала, но и о частоте. Это воз­можно благодаря тому, что опорное колебание порождается самим принимаемым сигналом, а не создается специальным генератором в месте приема.

2. Код с проверкой на чётность: процедура построения и основные характеристики.

Кодовых комбинаций данного кода всегда чётное число! Этот код является простейшим разделимым систематическим циклическим линейным кодом длины n с k = n-1 информационными и r =1 проверочным символом. Обозначается как (n,n-1)-код. Его комбинации обладают свойством цикличности, поэтому код является циклическим. В рамках ТЛ3 проверочный символ находится как сумма по модулю два всех информационных символов. Корректирующая способность кода: код обнаруживает ошибки любой нечетной кратности в пределах n.

Процедура обнаружения состоит в проверке на четность всей принятой комбинации.

Характеристики кода: Число информационных символов k Число проверочных символов r=1 Длина кода n = k+r Кодовое расстояние d=2 Относительная скорость передачи q = k/n Избыточность кода И = 1/k Вероятность появления ошибочной комбинации на выходе устройства обнаружения при вероятности перехода 1 в 0 и 0 в 1. вероятность приема неискаженных символов q=1-p равна: Р_ош = С²_n p² q^n-2 + C⁴_n p⁴ q^n-4 = С²₄ p² q^4-2 + C⁴₄ p⁴ q^4-4 Вер-ть необнаружения однократных и трёхкратных ошибок: Р_но = С¹_n p¹ q^n-1 + C³_n p³ q^n-3