6 Параметр, характеризующий нелинейную зависимость q( A ) = qx , не

вошёл в последнее уравнение. Граница абсолютной устойчивости определяем по параметрам линейной части системы (по выражению в скобках).

4.6 Определение границ дополнительной области устойчивости

Рассмотрим нелинейные системы, в которых факт устойчивости может быть установлен, если удовлетворяется критерий устойчивости линейной части

систем, а возможные значения r при нечетно-симметричной нелинейной ха-

0

рактеристике y = f(x) могут содержаться в интервале угла ограниченного прямыми r1 x и r2 x (смотри рисунок 4.13). Дополнительная область устойчивости определяется в зависимости от максимального и минимального значения коэффициента гармонической линеаризации для каждого вида нелинейной характеристики. Так интервал значений 0 ≤ q( A ) ≤ ∞ в действительности имеет

113

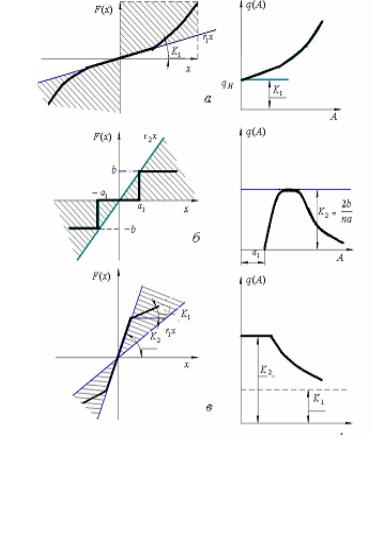
Рассмотрим наиболее характерные графики изменения коэффициентов гармонической линеаризации в зависимости от расположения нелинейной характеристики F(x) внутри сектора r1 x и r2 x (рисунок

4.14)

На рисунке 4.14 а показана нелинейная характеристика с возрастающим коэффициентом усиления, расположенная в секторе

Соответствующий коэффициент гармонической линеаризации изменяется в пределах

0 ≤ q(A) ≤ qнб = K2

На рисунке 4.14 в показана нелинейная характеристика усилителя с зоной насыщения, в которой коэффициент усиления уменьшается. Эта характеристика аппроксимирована кусочно-линейной зависимостью с коэффициентами усиления K 1 и K 2 , и расположена в секторе

r1 x ≤F( x )≤r2 x

Соответствующий коэффициент гармонической линеаризации изменяется в пределах

qнм = K1 ≤ q( A ) ≤ qнб = K2

Таким образом, каждый вид нелинейной характеристики имеет свой сектор расположения и свои предельные значения коэффициента линеаризации, что позволяет более точно определить условия устойчивости нелинейной системы. Е. П. Попов рекомендует этот расчет провести в следующем порядке [4].

114

Первый шаг. Границу области абсолютной устойчивости определять при 0 ≤ q( A) ≤ ∞ путем исключения гармонического коэффициента q( A) из урав-

нений

H n−1( q ) = 0; ∂Hn−1( q ) / ∂H =0

Это решение дает достаточные условия устойчивости при любой форме однозначной нелинейной характеристики и при любом интервале изменения коэффициента гармонической линеаризации.

Второй шаг. Получение дополнительной области устойчивости за счёт ограничения интервала фактически возможного изменения коэффициента гармонической линеаризации. Для этого в уравнение Hn−1(q) = 0 надо подставить

значения qнм (наименьшее) и qнб (наибольшее). Эти значения выражены через

параметры коэффициентов гармонической линеаризации (рисунок 4.14). Такое решение дает необходимые и достаточные условия устойчивости при заданной форме однозначной нелинейной характеристики.

Таким образом, по первому шагу определяется устойчивость нелинейной системы с некоторым запасом, когда не учитывается действительная граница нелинейности в секторе r1 x ≤ F( x ) ≤ r2 x .

По второму шагу проводится учет границ нелинейности. И чем более узкий сектор, где разместилась вся нелинейная характеристика, тем больше будет область дополнительной границы абсолютной устойчивости. Кроме этого, по условию Hn−1( q ) =0 при различных варьируемых параметрах линейной

части можно определить область периодических решений (режим автоколебаний). Рассмотрим этот метод на конкретном примере.

Пример 4.12 – Определить дополнительную область устойчивости в зависимости от K1 с учётом различного расположения нелинейной характеристики внутри сектора r1 x и r2 x по данным примера 4.11.

РЕШЕНИЕ

1 Определим значение Koc по уравнению границы области абсолютной устойчивости по критерию Гурвица H n−1(q) = 0 .

Hn−1( q ) =T1 +T2 +T1K2 (T1Koc −T2 K1 )q =0 T12 K2 Kocq = −(T1 +T2 ) +T1T2 K1K2q

В общем случае значение Koc в зависимости от ограничения интервала изменения q( A) от qнб до qнм определяется соотношением

115

Устойчивость системы при непериодических решениях остается в тех же пределах

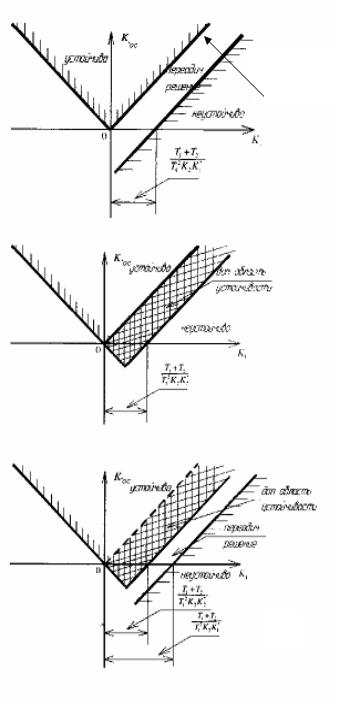
Это показано на рисунке 4.15 а 3 Для характеристики реле с

взоной нечувствительности (рисунок 4.14 б) имеется ограничение по q

непериодического решения. Области периодического решения нет. Это показано на рисунке 4.15 б.

116