
- •«Обработка изображений и распознавание образов» Визильтер Юрий Валентинович Методическое пособие-2010
- •Раздел 2. Распознавание образов. 165
- •1.1. Задачи и приложения машинного зрения. Примеры практических приложений.
- •Уровни и методы машинного зрения
- •Растровое изображение Изображение как двумерный массив данных
- •Алгебраические операции над изображениями
- •Физическая природа изображений
- •Изображения различных диапазонов длин волн
- •Изображения различной физической природы
- •Тип пикселя
- •Возможности и особенности системыPisoft
- •Базовые средства просмотра и анализа изображений и видеопоследовательностей
- •Алгебра изображений
- •Геометрические преобразования изображений
- •Устройства оцифровки и ввода изображений
- •Линейки и матрицы, сканеры и камеры
- •Геометрия изображения
- •Цифровые и аналоговые устройства
- •Пространственное разрешение
- •Программное обеспечение
- •Обработка цветных изображений
- •Цветовая модельRgb
- •Цветовая модель hsv
- •Цветовая модель yuv
- •Цветовая сегментация изображения
- •Гистограмма и гистограммная обработка изображений
- •Профиль вдоль линии и анализ профиля
- •Проекция и анализ проекции
- •Бинаризация полутоновых изображений
- •Сегментация многомодальных изображений
- •Выделение и описание областей
- •Выделение связных областей на бинарных изображениях
- •1. Отслеживающие алгоритмы на примере алгоритма обхода контура.
- •2. Сканируюющие алгоритмы.
- •1.3. Фильтрация. Выделение объектов при помощи фильтров
- •Оконная фильтрация изображений в пространственной области
- •Фильтрация бинарных изображений Модель шума «соль и перец»
- •Структура оконного фильтра
- •Логическая фильтрация помех
- •Бинарная медианная фильтрация
- •Бинарная ранговая фильтрация
- •Взвешенные ранговые фильтры
- •Анизотропная фильтрация
- •Расширение-сжатие (простая морфология)
- •Стирание бахромы
- •Нелинейная фильтрация полутоновых изображений
- •Ранговая оконная фильтрация
- •Минимаксная фильтрация
- •Задача выделения объектов интереса
- •Бинарные фильтры для выделения объектов
- •Метод нормализации фона
- •Скользящее среднее в окне
- •Гауссовская фильтрация
- •Преобразование Фурье. Линейная фильтрация в частотной области
- •Преобразование Фурье
- •Комплексное представление преобразования Фурье
- •Быстрое преобразование Фурье
- •Двумерное преобразование Фурье
- •Свертка с использованием преобразования Фурье
- •Фильтрация изображений в частотной области
- •Вейвлет-анализ
- •Пирамида изображений
- •Вейвлет-преобразование
- •Операторы вычисления производных
- •Операторы вычисления векторов градиентов
- •Операторы Марра и Лапласа
- •Постобработка контурного изображения Локализация края
- •Утончение контура
- •Сегментация полутоновых изображений
- •Пороговая и мультипороговая сегментация
- •Методы слияния, разбиения и слияния/разбиения областей
- •Способы описания выделенных областей
- •Текстурные признаки
- •1.6.Морфологические методы анализа сцен (по ю.П. Пытьеву) Методы обнаружения объектов, заданных эталонами
- •Согласованная фильтрация.
- •Корреляционное обнаружение.
- •Морфологический подход ю.П. Пытьева.
- •Форма изображения как инвариант преобразований изображений, отвечающих вариациям условий регистрации
- •Сравнение изображений по форме
- •Выделение отличий изображений по форме
- •Обнаружение объекта по его изображению и оценка его координат
- •*Морфология на базе кусочно-линейной интерполяции
- •Преобразование Хафа для поиска прямых
- •*Различные способы параметризации прямых
- •Преобразование Хафа для поиска окружностей
- •Анализ аккумулятора при поиске геометрических примитивов
- •Обобщенное преобразование Хафа
- •*Специализированная процедура голосования для поиска эллипсов
- •*Рекуррентное преобразование Хафа в скользящем окне
- •1.8.Математическая морфология (по ж. Серра)
- •Морфологические операции на бинарных изображениях
- •Морфологические операции на полутоновых изображениях
- •Морфологическое выделение «черт» и объектов
- •Морфологический спектр
- •Морфологические скелеты. Непрерывная бинарная морфология Непрерывная бинарная морфология
- •Непрерывное гранично-скелетное представление изображения
- •Обработка и использование скелета
- •*Обобщенные скелетные представления бинарных фигур
- •Алгоритмы утончения дискретного бинарного изображения
- •*Регуляризация скелетов
- •Типы нерегулярностей скелета
- •Устранение нерегулярностей
- •Регуляризация скелета по Тихонову
- •*Селективные морфологии
- •1.9. Анализ движения. Выделение движущихся объектов. Разность кадров. Вычитание фона. Анализ оптических потоков. Слежение за движущимися объектами. Корреляционное слежение.
- •Обучение с учителем. Детерминированные методы, основанные на «близости». Линейные решающие правила. Метод построения эталонов. Метод ближайшего соседа. Методkближайших соседей.
- •Линейные решающие правила
- •Метод построения эталонов
- •Методы ближайших соседей
- •Параметрические и непараметрические методы
- •Дискриминантные и моделирующие методы обучения
- •Способность распознавателя к обобщению. Регуляризация.
- •Байесовская теория решений. Случай двух классов. Классификаторы, разделяющие функции и поверхности решений. Вероятности ошибок. Разделяющие функции для случая нормальной плотности.
- •Дискриминантный анализ. Линейный дискриминант Фишера. Персептронная функция критерия. Линейный дискриминантный анализ (lda,дискриминант Фишера)
- •Персептрон Розенблатта
- •Анализ свидетельств
- •Байесовское объединение свидетельств
- •Структурное распознавание
- •Автоматизированное конструирование алгоритмов обнаружения объектов на основе преобразований модельных описаний объектов.
- •Нейросетевое распознавание
- •Нейронные сети ассоциативной памяти. Сети Хопфилда.
- •Многослойные персептроны. Оптимизационное обучение. Метод обратного распространения ошибки.
- •Многослойные персептроны. Правило Хебба.
- •*Связь с байесовским распознаванием
- •Сети встречного распространения. Самоорганизующиеся сети.
Байесовская теория решений. Случай двух классов. Классификаторы, разделяющие функции и поверхности решений. Вероятности ошибок. Разделяющие функции для случая нормальной плотности.
Говоря
о статистических методах распознавания,
мы предполагаем установление связи
между отнесением объекта к тому или
иному классу (образу) и вероятностью
ошибки при решении этой задачи. В ряде
случаев это сводится к определению
апостериорной вероятности принадлежности
объекта образу
![]() при условии, что признаки этого объекта
приняли значения
при условии, что признаки этого объекта
приняли значения![]() .
Начнём с байесовского решающего правила.
По формуле Байеса
.
Начнём с байесовского решающего правила.
По формуле Байеса

Здесь
![]() –
априорная вероятность предъявления к
распознаванию объекта
–
априорная вероятность предъявления к
распознаванию объекта![]() -го
образа:
-го
образа:
![]()
![]() .
.
для
каждого
![]()
![]() ,
,
при признаках с непрерывной шкалой измерений
 ,
,
при признаках с дискретной шкалой измерений
![]() .
.
При
непрерывных значениях признаков
![]() представляет из себя функцию плотности
вероятностей, при дискретных –
распределение вероятностей.
представляет из себя функцию плотности
вероятностей, при дискретных –
распределение вероятностей.
Распределения,
описывающие разные классы, как правило,
"пересекаются", то есть имеются
такие значения признаков
![]() ,
при которых
,
при которых
![]() .
.
В
таких случаях ошибки распознавания
неизбежны. Естественно, неинтересны
случаи, когда эти классы (образы) в
выбранной системе признаков
![]() неразличимы (при равных априорных
вероятностях решения можно выбирать
случайным отнесением объекта к одному
из классов равновероятным образом).
неразличимы (при равных априорных
вероятностях решения можно выбирать
случайным отнесением объекта к одному
из классов равновероятным образом).
В общем случае нужно стремиться выбрать решающие правила так, чтобы минимизировать риск потерь при распознавании.
Риск потерь определяется двумя компонентами: вероятностью ошибок распознавания и величиной "штрафа" за эти ошибки (потерями). Матрица ошибок распознавания:
 ,
,
где ![]() –
вероятность правильного распознавания;
–
вероятность правильного распознавания;
![]() –вероятность
ошибочного отнесения объекта
–вероятность
ошибочного отнесения объекта
![]() -го
образа к
-го
образа к![]() -му
(
-му
(![]() ).
).
Матрица потерь
![]()
 ,
,
где ![]() –
"премия" за правильное распознавание;
–
"премия" за правильное распознавание;
![]() –"штраф"
за ошибочное отнесение объекта
–"штраф"
за ошибочное отнесение объекта
![]() -го
образа к
-го
образа к![]() -му
(
-му
(![]() ).
).
Необходимо построить решающее правило так, чтобы обеспечить минимум математического ожидания потерь (минимум среднего риска). Такое правило называется байесовским.
Разобьём
признаковое пространство
![]() на
на![]() непересекающихся областей
непересекающихся областей![]() ,
каждая из которых соответствует
определённому образу.
,
каждая из которых соответствует
определённому образу.
Средний
риск при попадании реализаций
![]() -го
образа в области других образов равен
-го
образа в области других образов равен
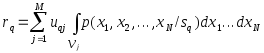 ,
,
![]() .
.
Здесь
предполагается, что все компоненты
![]() имеют непрерывную шкалу измерений (в
данном случае это непринципиально).
имеют непрерывную шкалу измерений (в
данном случае это непринципиально).
Величину
![]() можно назвать условным средним риском
(при условии, что совершена ошибка при
распознавании объекта
можно назвать условным средним риском
(при условии, что совершена ошибка при
распознавании объекта![]() -го
образа). Общий (безусловный) средний
риск определяется величиной
-го
образа). Общий (безусловный) средний
риск определяется величиной![]()
Решающие
правила (способы разбиения
![]() на
на![]()
![]() )
образуют множество
)
образуют множество![]() .
Наилучшим (байесовским) решающим правилом
является то, которое обеспечивает
минимальный средний риск
.
Наилучшим (байесовским) решающим правилом
является то, которое обеспечивает
минимальный средний риск![]() ,
где
,
где![]() –
средний риск при применении одного из
решающих правил, входящих в
–
средний риск при применении одного из
решающих правил, входящих в![]() .
.
Рассмотрим
упрощённый случай. Пусть
![]() ,
а
,
а![]() (
(![]() ).
В таком случае байесовское решающее
правило обеспечивает минимум вероятности
(среднего количества) ошибок распознавания.
Пусть
).
В таком случае байесовское решающее
правило обеспечивает минимум вероятности
(среднего количества) ошибок распознавания.
Пусть![]() .
Вероятность ошибки первого рода (объект
1-го образа отнесён ко второму образу)
.
Вероятность ошибки первого рода (объект
1-го образа отнесён ко второму образу)
![]() ,
,
где
![]() –
вероятность ошибки второго рода
–
вероятность ошибки второго рода
![]() .
.
Средние ошибки
![]() .
.
Так как
![]() ,
то
,
то
![]()
и
![]() .
.
ясно,
что минимум
![]() будет иметь минимум в том случае, если
подынтегральное выражение в области
будет иметь минимум в том случае, если
подынтегральное выражение в области![]() будет строго отрицательным, то есть в
будет строго отрицательным, то есть в![]()
![]() .
В области
.
В области![]() должно выполняться противоположное
неравенство. Это и есть байесовское
решающее правило для рассматриваемого
случая. Оно может быть записано иначе:
должно выполняться противоположное
неравенство. Это и есть байесовское
решающее правило для рассматриваемого
случая. Оно может быть записано иначе:![]() ;
величина
;
величина![]() ,
рассматриваемая как функция от
,
рассматриваемая как функция от![]() ,
называется правдоподобием
,
называется правдоподобием![]() при данном
при данном![]() ,
а
,
а![]() –
отношением правдоподобия. Таким образом,
байесовское решающее правило можно
сформулировать как рекомендацию выбирать
решение
–
отношением правдоподобия. Таким образом,
байесовское решающее правило можно
сформулировать как рекомендацию выбирать
решение![]() в случае, если отношение правдоподобия
превышает определённое пороговое
значение, не зависящее от наблюдаемого
в случае, если отношение правдоподобия
превышает определённое пороговое
значение, не зависящее от наблюдаемого![]() .
.
Без
специального рассмотрения укажем, что
если число распознаваемых классов
больше двух (![]() ),
решение в пользу класса (образа)
),
решение в пользу класса (образа)![]() принимается в области
принимается в области![]() ,
в которой для всех
,
в которой для всех![]()
![]() .
.
После
вычисления апостериорных вероятностей
принадлежности неизвестного объекта
с параметрами
![]() каждому из образов
каждому из образов![]() ,
,![]() ,
отрезок прямой длиной единица разбивают
на
,
отрезок прямой длиной единица разбивают
на![]() интервалов с длинами, численно равными
интервалов с длинами, численно равными![]() ,
и каждому интервалу ставят в соответствие
этот образ. Затем с помощью датчика
случайных (псевдослучайных) чисел,
равномерно распределённых на
,
и каждому интервалу ставят в соответствие
этот образ. Затем с помощью датчика
случайных (псевдослучайных) чисел,
равномерно распределённых на![]() ,
генерируют число, определяют интервал,
в который оно попало, и относят
распознаваемый объект к тому образу,
которому соответствует данный интервал.
Понятно, что такое решающее правило не
может быть лучше байесовского, но при
больших значениях отношения правдоподобия
ненамного ему уступает, а в реализации
может оказаться достаточно простым
(например, метод ближайшего соседа).
,
генерируют число, определяют интервал,
в который оно попало, и относят
распознаваемый объект к тому образу,
которому соответствует данный интервал.
Понятно, что такое решающее правило не
может быть лучше байесовского, но при
больших значениях отношения правдоподобия
ненамного ему уступает, а в реализации
может оказаться достаточно простым
(например, метод ближайшего соседа).
Байесовское решающее правило реализуется в компьютерах в основном двумя способами.
1. Прямое вычисление апостериорных вероятностей
 ,
,
где  –
вектор значений параметров распознаваемого
объекта и выбор максимума. Решение
принимается в пользу того образа, для
которого
–
вектор значений параметров распознаваемого
объекта и выбор максимума. Решение
принимается в пользу того образа, для
которого![]() максимально. Иными словами, байесовское
решающее правило реализуется решением
задачи
максимально. Иными словами, байесовское
решающее правило реализуется решением
задачи![]() .
.
Если
пойти на дальнейшее обобщение и допустить
наличие матрицы потерь общего вида, то
условный риск можно определить по
формуле
![]() ,
,![]() .
Здесь первый член определяет "поощрение"
за правильное распознавание, а второй –
"наказание" за ошибку. Байесовское
решающее правило в данном случае состоит
в решении задачи
.
Здесь первый член определяет "поощрение"
за правильное распознавание, а второй –
"наказание" за ошибку. Байесовское
решающее правило в данном случае состоит
в решении задачи

2. "Топографическое"
определение области
![]() ,
в которую попал вектор
,
в которую попал вектор![]() значений признаков, описывающих
распознаваемый объект.
значений признаков, описывающих
распознаваемый объект.
Такой
подход используют в тех случаях, когда
описание областей
![]() достаточно компактно, а процедура
определения области, в которую попал
достаточно компактно, а процедура
определения области, в которую попал![]() ,
проста. Иными словами, данный подход
естественно использовать, когда в
вычислительном отношении он эффективнее
(проще), чем прямое вычисление апостериорных
вероятностей.
,
проста. Иными словами, данный подход
естественно использовать, когда в
вычислительном отношении он эффективнее
(проще), чем прямое вычисление апостериорных
вероятностей.

Рис. 19. Байесовское решающее правило для нормально распределённых признаков с равными ковариационными матрицами
Так,
например (доказательство приводить не
будем), если классов два, их априорные
вероятности одинаковы,
![]() и
и![]() –
нормальные распределения с одинаковыми
ковариационными матрицами (отличаются
только векторами средних), то байесовская
разделяющая граница – гиперплоскость.
Запоминается она значениями коэффициентов
линейного уравнения. При распознавании
какого-либо объекта в уравнение
подставляют значения признаков
–
нормальные распределения с одинаковыми
ковариационными матрицами (отличаются
только векторами средних), то байесовская
разделяющая граница – гиперплоскость.
Запоминается она значениями коэффициентов
линейного уравнения. При распознавании
какого-либо объекта в уравнение
подставляют значения признаков![]() этого объекта и по знаку (плюс или минус)
получаемого решения относят объект к
этого объекта и по знаку (плюс или минус)
получаемого решения относят объект к![]() или
или![]() (рис. 19).
(рис. 19).
Если
у классов
![]() и
и![]() ковариационные матрицы
ковариационные матрицы![]() и
и![]() не только одинаковы, но и диагональны,
то байесовским решением является
отнесение объекта к тому классу, евклидово
расстояние до эталона которого минимально
(рис. 20).
не только одинаковы, но и диагональны,
то байесовским решением является
отнесение объекта к тому классу, евклидово
расстояние до эталона которого минимально
(рис. 20).

Рис. 20. Байесовское решающее правило для нормально распределённых признаков с равными диагональными ковариационными матрицами (элементы диагоналей одинаковы)
Таким образом, мы убеждаемся в том, что некоторые решающие правила, ранее рассмотренные нами как эмпирические (детерминированные, эвристические), имеют вполне чёткую статистическую трактовку. Более того, в ряде конкретных случаев они являются статистически оптимальными.
