Свертка с использованием преобразования Фурье

Свертка функций s(t) и r(t) определяется, как

На практике приходится иметь дело с дискретной сверткой, в которой непрерывные функции заменяются наборами значений в узлах равномерной сетки (обычно берется целочисленная сетка):

Здесь –N и P определяют диапазон, за пределами которого r(t) = 0.

При вычислении свертки с помощью преобразования Фурье используется свойство преобразования Фурье, согласно которому произведение образов функций в частотной области эквивалентно свертке этих функций во временной области.

Для вычисления сверки необходимо преобразовать исходные данные в частотную область, то есть вычислить их преобразование Фурье, перемножить результаты преобразования и выполнить обратное преобразование Фурье, восстановив исходное представление.

Единственная тонкость в работе алгоритма связана с тем, что в случае дискретного преобразования Фурье (в отличие от непрерывного) происходит свертка двух периодических функций, то есть наши наборы значений задают именно периоды этих функций, а не просто значения на каком-то отдельном участке оси. То есть алгоритм считает, что за точкой x_N идет не ноль, а точкаx₀, и так далее по кругу. Поэтому, чтобы свертка корректно считалась, необходимо приписать к сигналу достаточно длинную последовательность нулей.

Фильтрация изображений в частотной области

Линейные методы фильтрации относятся к числу хорошо структурированных методов, для которых разработаны эффективные вычислительные схемы, основанные на быстрых алгоритмах свертки и спектральном анализе. В общем виде линейные алгоритмы фильтрации выполняют преобразование вида:

f'(x,y) = f(–x,–y)K(,)dd,

где K(,) – ядро линейного преобразования.

При дискретном представлении сигнала интеграл в данной формуле вырождается во взвешенную сумму отсчетов исходного изображения в пределах некоторой апертуры. При этом выбор ядра K(,) в соответствии с тем или иным критерием оптимальности может привести к ряду полезных свойств (гауссовское сглаживание при регуляризации задачи численного дифференцирования изображения и др.).

Наиболее эффективно линейные методы обработки реализуются в частотной области.

Использование Фурье образа изображения для выполнения операций фильтрации обусловлено прежде всего более высокой производительностью таких операций. Как правило, выполнение прямого и обратного двумерного преобразования Фурье и умножение на коэффициенты Фурье образа фильтра занимает меньше времени, чем выполнение двумерной свертки исходного изображения.

Алгоритмы фильтрации в частотной области основываются на теореме о свертке. В двумерном случае преобразование свертки выглядит следующим образом:

,

где G– Фурье образ результата свертки, Н – Фурье образ фильтра, аF– Фурье образ исходного изображения. То есть в частотной области двумерная свертка заменяется поэлементным перемножением образов исходного изображения и соответствующего фильтра.

Для выполнения свертки необходимо выполнить следующие действия:

1. Умножить элементы исходного изображения на 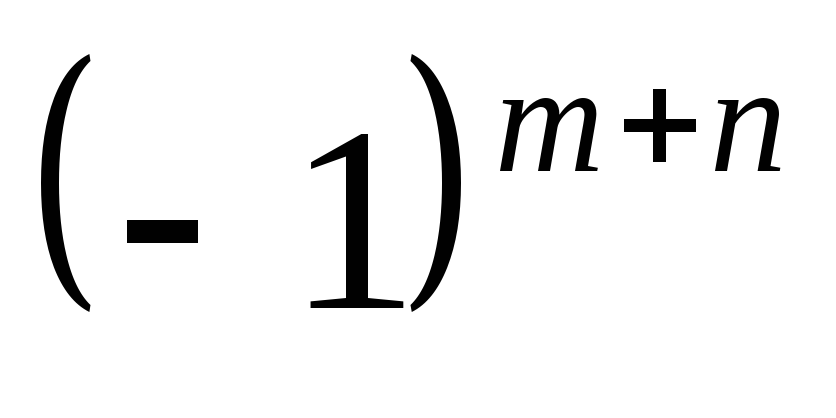, для центрирования Фурье образа.

2. Вычислить F(u,v) используя БПФ.

3. Умножить F(u,v) на функцию фильтраH(u,v).

4. Вычислить обратное преобразование Фурье.

5. Умножить вещественную часть обратного преобразования на .

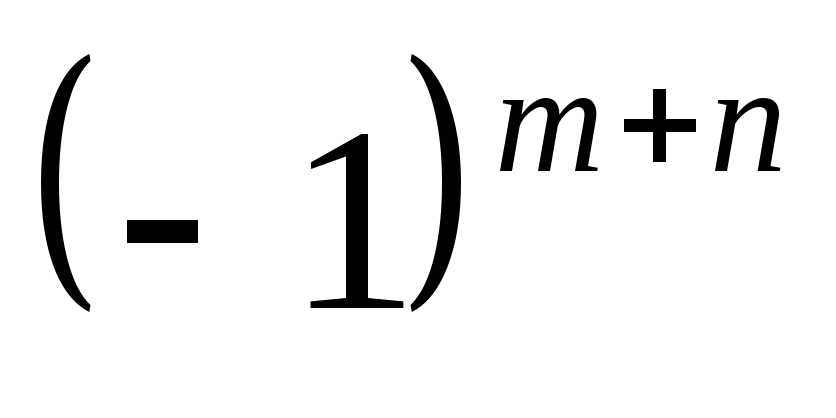Как правило, фильтры описываются вещественными функциями, в этом случае каждый компонент Hумножается на соответствующие элементы действительной и мнимой части Фурье образа изображения. Если исходная функцияf(x,y) и фильтрHне комплексные, то результат сверткиg(x,y) также должен быть вещественной функцией. Однако на практике обратное преобразование содержит паразитную мнимую составляющую, которую надо отбросить.

Связь между функцией фильтра в частотной и пространственной области можно определить, используя теорему о свертке:

Свертка функции с импульсной функцией может быть представлена следующим образом:

Фурье преобразование импульсной функции:

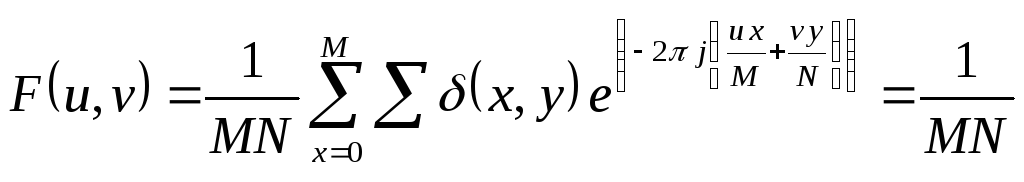
пусть f(x,y) =δ(x,y) тогда свертка

Из этих выражений видно, что функции фильтра в частотной и пространственной областях взаимосвязаны через преобразование Фурье. Для данной функции фильтра в частотной области всегда можно найти соответствующий фильтр в пространственной области, применив обратное преобразование Фурье. Тоже верно и для обратного случая. Используя данную взаимосвязь можно определить процедуру синтеза пространственных фильтров:

1. Определяем требуемые характеристики (форму) фильтра в частотной области.

2. Выполняем обратное преобразование Фурье.

3. Полученный фильтр можно использовать как маску для пространственной свертки, при этом размеры маски можно уменьшить по сравнению с размерами исходного фильтра.

Идеальный фильтр низких частотH(u,v) имеет вид:

H(u,v) = 1, если D(u,v) < Do

H(u,v) = 0, еслиD(u,v)Do, где–

расстояние от центра частотной плоскости.

После свертки с этим фильтром на результирующем изображении появляются паразитные искажения в виде полутоновых ложных границ.

Идеальный высокочастотный фильтрполучается путем инверсии идеального низкочастотного фильтра:

h(u,v) = 1–H(u,v).

Здесь происходит полное подавление низкочастотных компонент при сохранении высокочастотных. Однако как и в случае идеального низкочастотного фильтра, его применение чревато появлением существенных искажений.

Для синтеза фильтров с минимальными искажениями используются различные подходы. Одним из них, является синтез фильтров на основе экспоненты. Такие фильтры привносят минимальные искажения в результирующее изображение и удобны для синтеза в частотной области.

Широко используемым при обработке изображений является семейство фильтров на основании вещественной функции Гаусса.

Низкочастотный гауссовский фильтримеет вид:

и

Чем уже профиль фильтра в частотной области (чем больше σ), тем он шире в пространственной.

Высокочастотный гауссовский фильтримеет вид:

В двумерном случае низкочастотныйфильтр гаусса выглядит следующим образом:

,

Высокочастотныйгауссовский фильтр имеет вид:

Рассмотрим пример фильтрации изображения (рис. 3.2.1) в частотной области

(рис. 3.3.17 – 3.3.22). Заметим, что частотная фильтрация изображения может иметь смысл как сглаживания (низкочастотная фильтрация), так и выделения контуров и мелкоразмерных объектов (высокочастотная фильтрация).

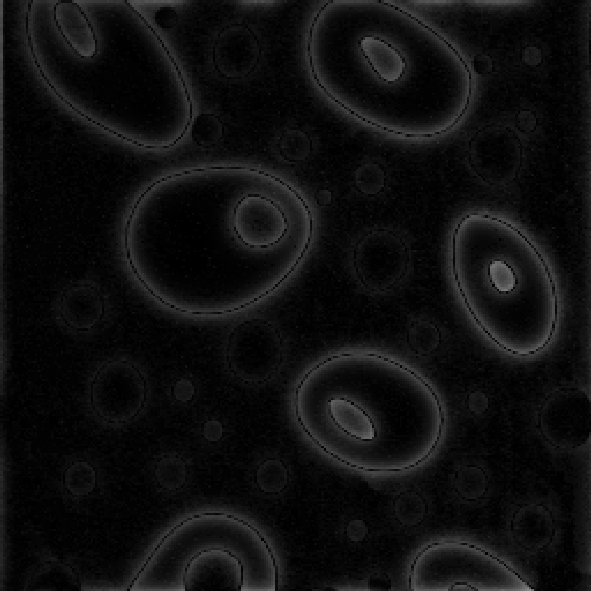
@Рис. 3.3.17. Низкочастотная фильтрация @Рис. 3.3.18. Высокочастотная

с параметрами (10,10) фильтрация с параметрами (10,10)

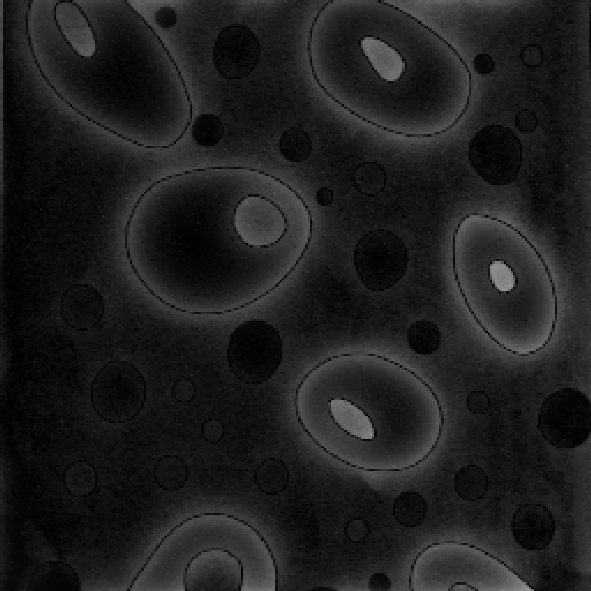
@Рис. 3.3.19. Низкочастотная фильтрация @Рис. 3.3.20. Высокочастотная

с параметрами (50,50) фильтрация с параметрами (50,50)

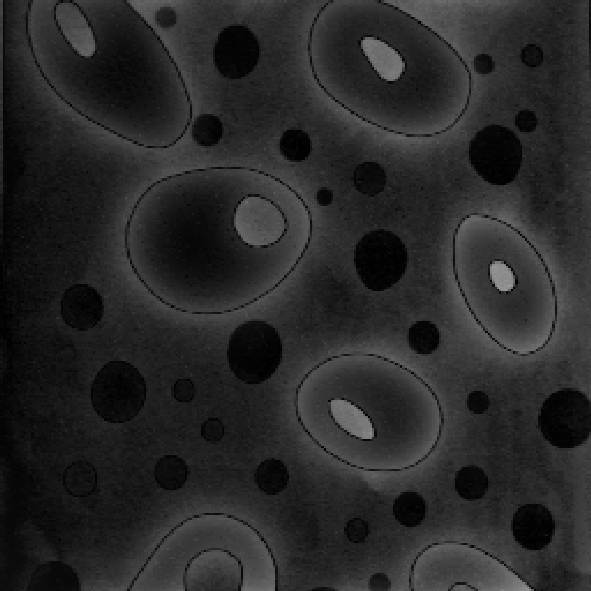
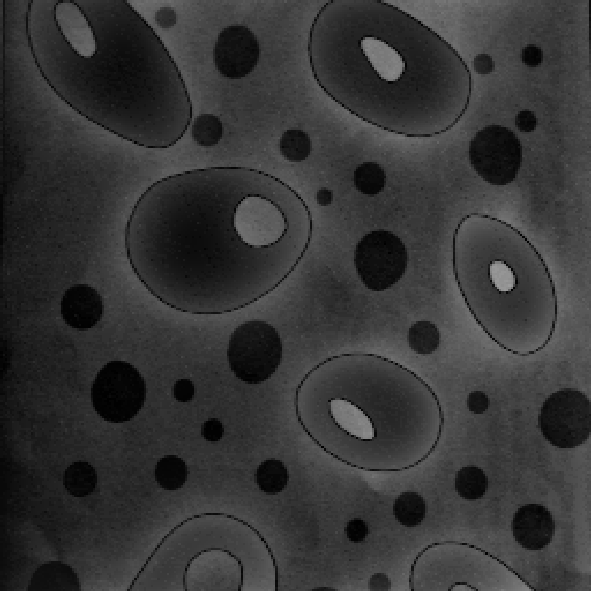
@Рис. 3.3.21. Высокочастотная фильтрация @Рис. 3.3.22. Высокочастотная

с параметрами (100,100) фильтрация с параметрами (200,200)

Как видно из рис. 3.3.17, 3.3.19 по мере нарастания «мощности» фильтрации в низкочастотной составляющей изображения все сильнее проявляется эффект «кажущейся расфокусировки» или размытияизображения. В то же время, в высокочастотную составляющую, где в начале наблюдаются лишь контура объектов, постепенно переходит большая часть информационного содержания изображения (рис. 3.3.18, 3.3.20 – 3.3.22).

Рассмотрим теперь поведение высокочастотных и низкочастотных фильтров

(рис. 3.3.23 – 3.3.28) в присутствии аддитивного гауссовского шума на изображении (рис. 3 3.7).

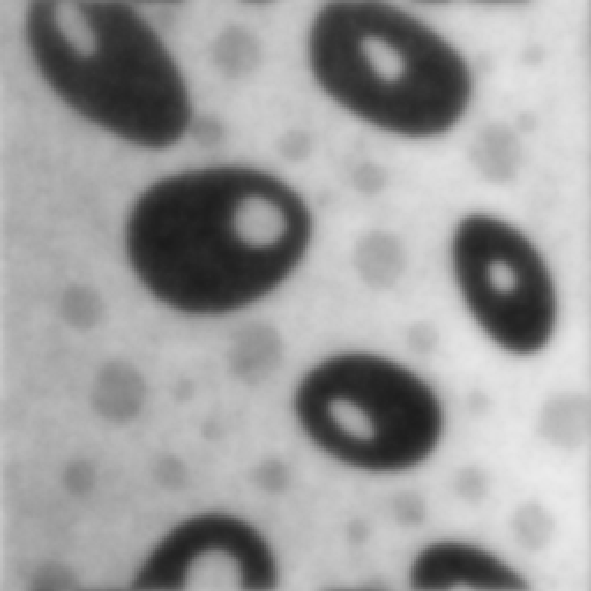
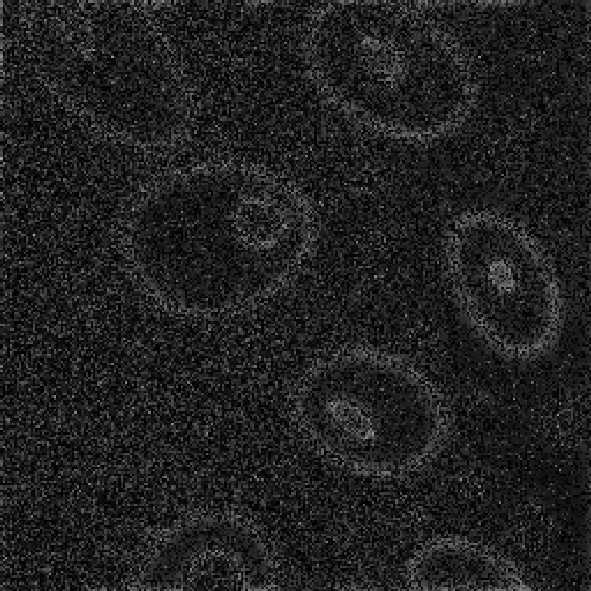
@Рис. 3.3.23. Низкочастотная фильтрация @Рис. 3.3.24. Высокочастотная

с параметрами (10,10) фильтрация с параметрами (10,10)

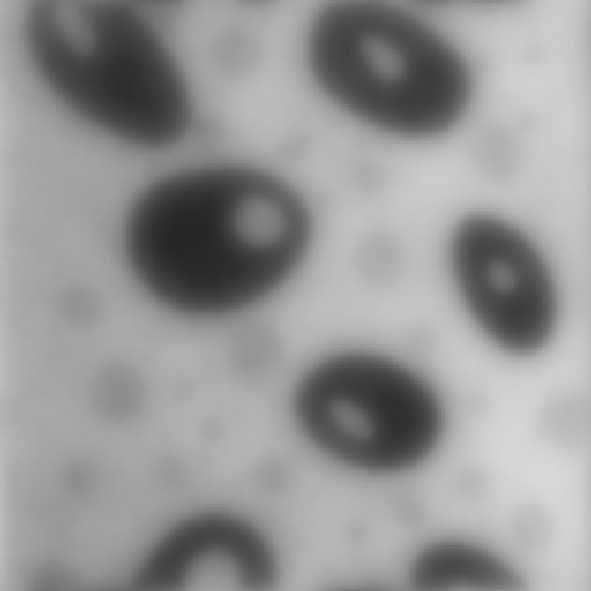
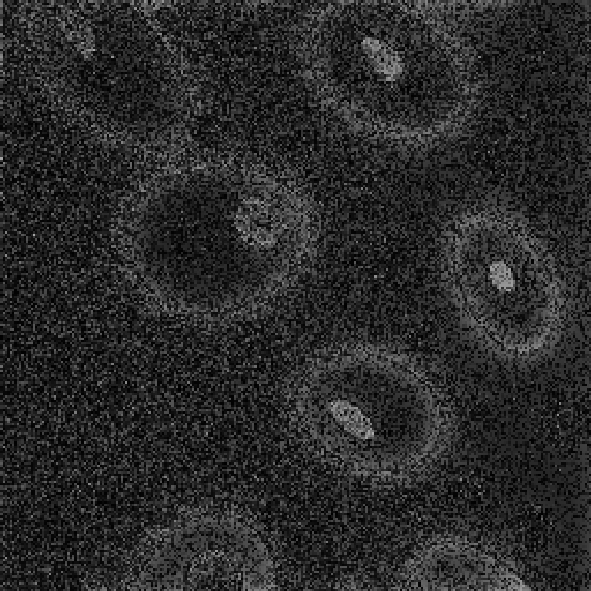
@Рис. 3.3.25. Низкочастотная фильтрация @Рис. 3.3.26. Высокочастотная

с параметрами (50,50) фильтрация с параметрами (50,50)

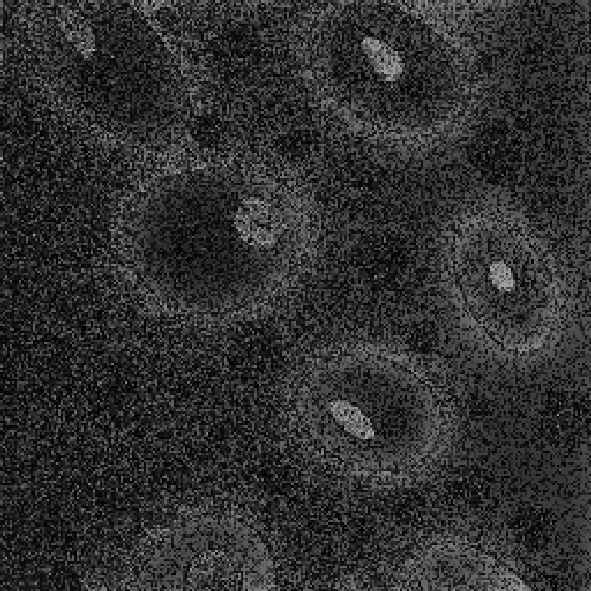
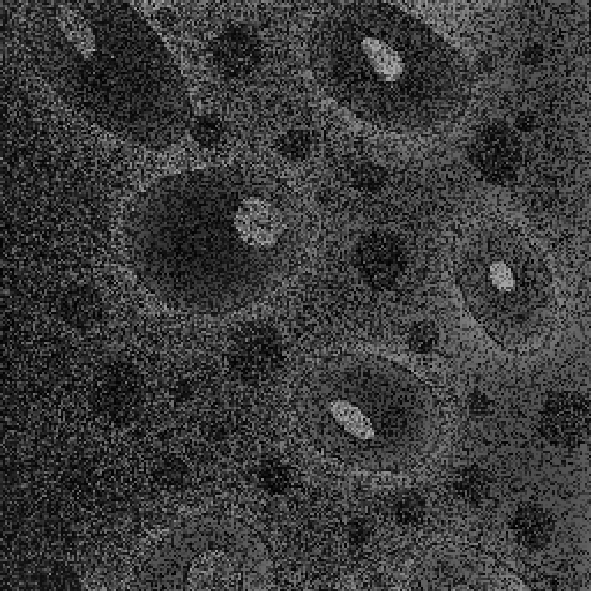
@Рис. 3.3.27. Высокочастотная фильтрация @Рис. 3.3.28. Высокочастотная

с параметрами (100,100) фильтрация с параметрами (200,200)

Как видно из рис. 3.3.23 – 3.3.25, свойства низкочастотных фильтров по подавлению аддитивной случайной помехи аналогичны свойствам ранее рассмотренных линейных фильтров – при достаточной мощности фильтра помехи подавляются, однако платой за это является сильное размытие контуров и «расфокусировка» всего изображения. Высокочастоная составляющая зашумленного изображения перестает быть информативной, так как помимо контурной и объектовой информации там теперь также полностью присутствует и шумовая компонента (рис. 3.3.27, 3.3.28).

Применение частотных методов наиболее целесообразно в случае, когда известны статистическая модель шумового процесса или/и оптическая передаточная функция канала передачи изображения. Учесть такие априорные данные удобно, выбрав в качестве восстанавливающего фильтра обобщенный управляемый (параметрами и) фильтр следующего вида:

где 0 < < 1, 0 << 1 назначаемые параметры фильтра, P(w₁,w₂) – передаточная функция системы, Q(w₁,w₂) – стабилизатор фильтра, согласованный с энергетическим спектром фона. Выбор параметров= 1,= 0 приводит к чисто инверсной фильтрации,== 1 квинеровской фильтрации, что позволяет получить изображение, близкое к истинному в смысле минимума СКО при условии, что спектры плотности мощности изображения и его шумовой компоненты априорно известны. Для дальнейшего улучшения эффекта сглаживания в алгоритм линейной (винеровской) фильтрации вводят адаптацию, основанную на оценке локальных статистик: математического ожиданияM[(P)]и дисперсии(P).Этот алгоритм эффективно фильтрует засоренные однородные поверхности (области) фона. Однако при попадании в скользящее окно обработки неоднородных участков фона импульсная характеристика фильтра сужается ввиду резкого изменения локальных статистик и эти неоднородности (контура, пятна) передаются практически без расфокусировки, свойственной неадаптивным методам линейной фильтрации.

К достоинствам методов линейной фильтрации следует отнести их ясный физический смысл и простоту анализа результатов. Однако при резком ухудшении соотношения сигнал/шум при возможных вариантах площадного зашумления и наличии высокоамплитудного импульсного шума линейные методы предварительной обработки могут оказаться недостаточными. В этой ситуации значительно более мощными оказываются нелинейные методы.