Скользящее среднее в окне

Простейшим видом линейной оконной фильтрации в пространственной области является скользящее среднеев окне. Результатом такой фильтрации является значение математического ожидания, вычисленное по всем пикселям окна. Математически это эквивалентно свертке с маской, все элементы которой равны 1/n, гдеn– число элементов маски. Например, маска скользящего среднего размера 33 имеет вид:



Рассмотрим пример фильтрации зашумленного полутонового изображения фильтром «скользяшее среднее». Изображения зашумлены гауссовским аддитивным шумом (рис. 3.2.2 – 3.2.8).

На рис. 3.3.1 – 3.3.6 приводятся примеры фильтрации полутонового изображения с различными степенями зашумления средним фильтром с размером окна 33. Как видно из примера, фильтр «скользящее среднее» обладает меньшей способностью к подавлению шумовой компоненты по сравнению с ранее рассмотренным медианным фильтром 33.

@Рис. 3.3.1. Слабая степень зашумления @Рис. 3.3.2. Результат фильтрации исходного изображения средним (avr) 33

@Рис. 3.3.3. Средняя степень зашумления @Рис. 3.3.4. Результат фильтрации исходного изображения avr33

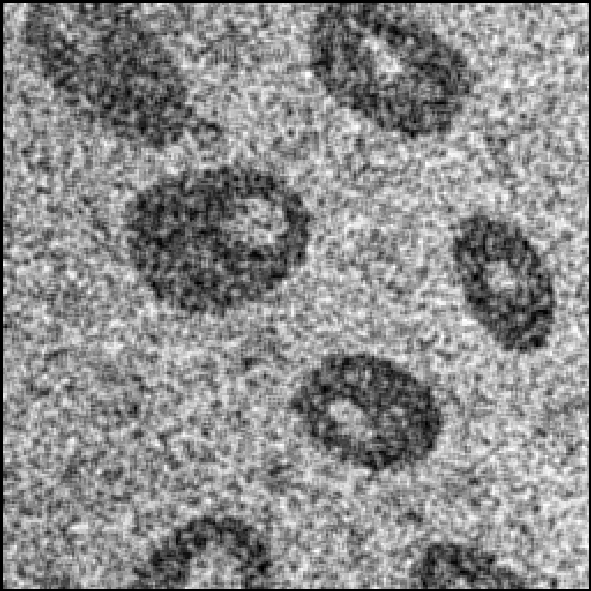
@Рис. 3.3.5. Сильная степень зашумления @Рис. 3.3.6. Результат фильтрации исходного изображения avr33

Рассмотрим скользящее среднее с бо€льшими размерами окна фильтрации. На рис. 3.2.23 – 3.2.28 приводится пример медианной фильтрации с различными размерами апертуры.

Как видно из рис. 3.3.7 – 3.3.12, с увеличением размера окна растет способность медианного фильтра подавлять шумовую компоненту. Однако при этом нарастает и эффект кажущейся «расфокусировки» изображения (рис. 3.3.11, 3.3.12) за счет размытия краев видимых объектов. Этого специфически присущего линейным фильтрам эффекта размытия мы также не наблюдали в случае нелинейной ранговой фильтрации.

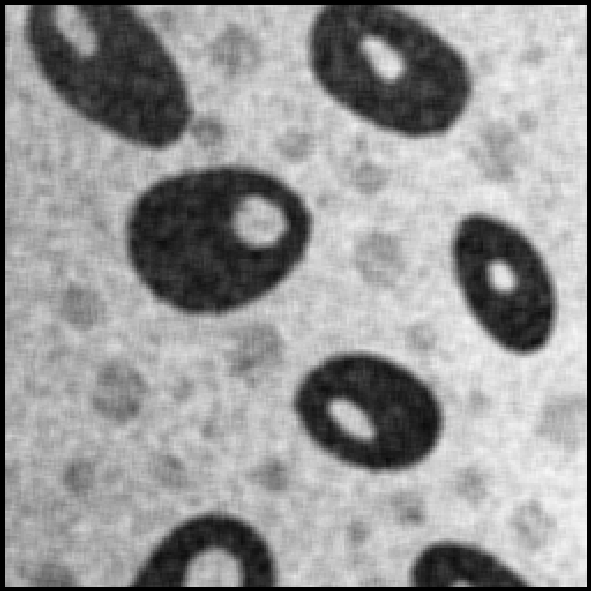
@Рис. 3.3.7. Зашумленное изображение @Рис. 3.3.8. Результат средней линейной фильтрации

avr55

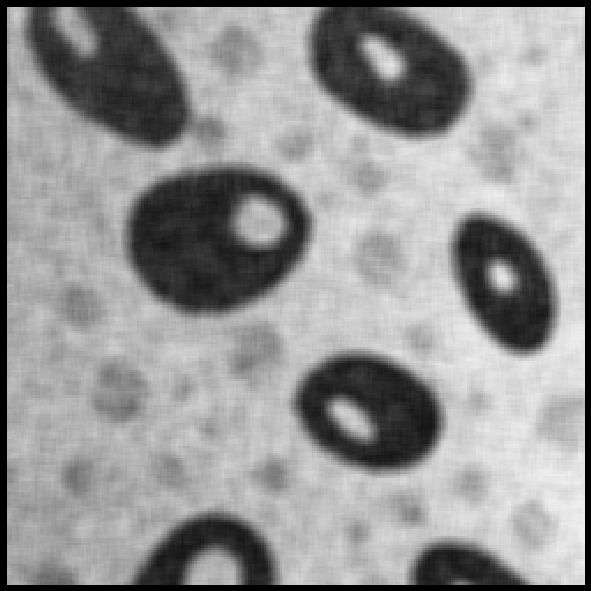
@Рис. 3.3.9. Результат средней линейной @Рис. 3.3.10. Результат средней линейной фильтрации

avr77 фильтрацииavr99

@Рис. 3.3.11. Результат средней линейной @Рис. 3.3.12. Результат средней

фильтрации avr1515 линейной фильтрацииavr3131

Гауссовская фильтрация

В предыдущем разделе мы рассмотрели «вырожденный» случай линейной фильтрации с однородной маской. Между тем, сама идея свертки изображения с весовой матрицей аналогична ранее рассмотренной идее введения весовой матрицы во взвешенных процентильных фильтрах. Повысить устойчивость результатов фильтрации на краях областей можно, если придать более близким точкам окрестности большее влияние на окончательный результат, чем дальним. Примером реализации этой идеи для окна размера 33 является следующая маска:



Такая маска называется Гауссовой, соответственно и использующий ее линейный фильтр также называется гауссовым. Используя дискретные приближения двумерной гауссовой функции можно получить и другие гауссовы ядра большего размера. Обратите внимание на то, чтосглаживающиеилифильтрующиемаски линейных фильтров должны иметь сумму всех элементов равную 1. Данноеусловие нормировкигарантирует адекватный отклик фильтра на постоянный сигнал (постоянное изображениеIm[x,y] =const).

На рис. 3.3.13 – 3.3.15 приведен пример гауссовой линейной фильтрации зашумленного изображения.

@Рис. 3.3.13. Зашумленное @Рис. 3.3.14. Результат @Рис. 3.3.15. Результат изображение гауссовой линейной гауссовой линейной фильтрации gauss33 фильтрацииgauss55