
- •«Обработка изображений и распознавание образов» Визильтер Юрий Валентинович Методическое пособие-2010
- •Раздел 2. Распознавание образов. 165
- •1.1. Задачи и приложения машинного зрения. Примеры практических приложений.
- •Уровни и методы машинного зрения
- •Растровое изображение Изображение как двумерный массив данных
- •Алгебраические операции над изображениями
- •Физическая природа изображений
- •Изображения различных диапазонов длин волн
- •Изображения различной физической природы
- •Тип пикселя
- •Возможности и особенности системыPisoft
- •Базовые средства просмотра и анализа изображений и видеопоследовательностей
- •Алгебра изображений
- •Геометрические преобразования изображений
- •Устройства оцифровки и ввода изображений
- •Линейки и матрицы, сканеры и камеры
- •Геометрия изображения
- •Цифровые и аналоговые устройства
- •Пространственное разрешение
- •Программное обеспечение
- •Обработка цветных изображений
- •Цветовая модельRgb
- •Цветовая модель hsv
- •Цветовая модель yuv
- •Цветовая сегментация изображения
- •Гистограмма и гистограммная обработка изображений
- •Профиль вдоль линии и анализ профиля
- •Проекция и анализ проекции
- •Бинаризация полутоновых изображений
- •Сегментация многомодальных изображений
- •Выделение и описание областей
- •Выделение связных областей на бинарных изображениях
- •1. Отслеживающие алгоритмы на примере алгоритма обхода контура.
- •2. Сканируюющие алгоритмы.
- •1.3. Фильтрация. Выделение объектов при помощи фильтров
- •Оконная фильтрация изображений в пространственной области
- •Фильтрация бинарных изображений Модель шума «соль и перец»
- •Структура оконного фильтра
- •Логическая фильтрация помех
- •Бинарная медианная фильтрация
- •Бинарная ранговая фильтрация
- •Взвешенные ранговые фильтры
- •Анизотропная фильтрация
- •Расширение-сжатие (простая морфология)
- •Стирание бахромы
- •Нелинейная фильтрация полутоновых изображений
- •Ранговая оконная фильтрация
- •Минимаксная фильтрация
- •Задача выделения объектов интереса
- •Бинарные фильтры для выделения объектов
- •Метод нормализации фона
- •Скользящее среднее в окне
- •Гауссовская фильтрация
- •Преобразование Фурье. Линейная фильтрация в частотной области
- •Преобразование Фурье
- •Комплексное представление преобразования Фурье
- •Быстрое преобразование Фурье
- •Двумерное преобразование Фурье
- •Свертка с использованием преобразования Фурье
- •Фильтрация изображений в частотной области
- •Вейвлет-анализ
- •Пирамида изображений
- •Вейвлет-преобразование
- •Операторы вычисления производных
- •Операторы вычисления векторов градиентов
- •Операторы Марра и Лапласа
- •Постобработка контурного изображения Локализация края
- •Утончение контура
- •Сегментация полутоновых изображений
- •Пороговая и мультипороговая сегментация
- •Методы слияния, разбиения и слияния/разбиения областей
- •Способы описания выделенных областей
- •Текстурные признаки
- •1.6.Морфологические методы анализа сцен (по ю.П. Пытьеву) Методы обнаружения объектов, заданных эталонами
- •Согласованная фильтрация.
- •Корреляционное обнаружение.
- •Морфологический подход ю.П. Пытьева.
- •Форма изображения как инвариант преобразований изображений, отвечающих вариациям условий регистрации
- •Сравнение изображений по форме
- •Выделение отличий изображений по форме
- •Обнаружение объекта по его изображению и оценка его координат
- •*Морфология на базе кусочно-линейной интерполяции
- •Преобразование Хафа для поиска прямых
- •*Различные способы параметризации прямых
- •Преобразование Хафа для поиска окружностей
- •Анализ аккумулятора при поиске геометрических примитивов
- •Обобщенное преобразование Хафа
- •*Специализированная процедура голосования для поиска эллипсов
- •*Рекуррентное преобразование Хафа в скользящем окне
- •1.8.Математическая морфология (по ж. Серра)
- •Морфологические операции на бинарных изображениях
- •Морфологические операции на полутоновых изображениях
- •Морфологическое выделение «черт» и объектов
- •Морфологический спектр
- •Морфологические скелеты. Непрерывная бинарная морфология Непрерывная бинарная морфология
- •Непрерывное гранично-скелетное представление изображения
- •Обработка и использование скелета
- •*Обобщенные скелетные представления бинарных фигур
- •Алгоритмы утончения дискретного бинарного изображения
- •*Регуляризация скелетов
- •Типы нерегулярностей скелета
- •Устранение нерегулярностей
- •Регуляризация скелета по Тихонову
- •*Селективные морфологии
- •1.9. Анализ движения. Выделение движущихся объектов. Разность кадров. Вычитание фона. Анализ оптических потоков. Слежение за движущимися объектами. Корреляционное слежение.
- •Обучение с учителем. Детерминированные методы, основанные на «близости». Линейные решающие правила. Метод построения эталонов. Метод ближайшего соседа. Методkближайших соседей.
- •Линейные решающие правила
- •Метод построения эталонов
- •Методы ближайших соседей
- •Параметрические и непараметрические методы
- •Дискриминантные и моделирующие методы обучения
- •Способность распознавателя к обобщению. Регуляризация.
- •Байесовская теория решений. Случай двух классов. Классификаторы, разделяющие функции и поверхности решений. Вероятности ошибок. Разделяющие функции для случая нормальной плотности.
- •Дискриминантный анализ. Линейный дискриминант Фишера. Персептронная функция критерия. Линейный дискриминантный анализ (lda,дискриминант Фишера)
- •Персептрон Розенблатта
- •Анализ свидетельств
- •Байесовское объединение свидетельств
- •Структурное распознавание
- •Автоматизированное конструирование алгоритмов обнаружения объектов на основе преобразований модельных описаний объектов.
- •Нейросетевое распознавание
- •Нейронные сети ассоциативной памяти. Сети Хопфилда.
- •Многослойные персептроны. Оптимизационное обучение. Метод обратного распространения ошибки.
- •Многослойные персептроны. Правило Хебба.
- •*Связь с байесовским распознаванием
- •Сети встречного распространения. Самоорганизующиеся сети.
1.3. Фильтрация. Выделение объектов при помощи фильтров
ФИЛЬТРАЦИЯ БИНАРНЫХ ИЗОБРАЖЕНИЙ. МОДЕЛЬ ШУМА "СОЛЬ И ПЕРЕЦ". ЛОГИЧЕСКАЯ ФИЛЬТРАЦИЯ. РАНГОВАЯ ФИЛЬТРАЦИЯ. БИНАРНАЯ МЕДИАНА. СТРУКТУРНЫЕ ИСКАЖЕНИЯ. РАСШИРЕНИЕ И СЖАТИЕ БИНАРНЫХ ИЗОБРАЖЕНИЙ. ВЫДЕЛЕНИЕ МЕЛКОРАЗМЕРНЫХ ОБЪЕКТОВ. ПЕЛЕНГ. ПЕЛЕНГ С ОКАЙМЛЕНИЕМ. РЕКУРРЕНТНАЯ РЕАЛИЗАЦИЯ БИНАРНЫХ ФИЛЬТРОВ.
НЕЛИНЕЙНАЯ ФИЛЬТРАЦИЯ ПОЛУТОНОВЫХ ИЗОБРАЖЕНИЙ. ОБОБЩЕНИЕ МЕТОДОВ БИНАРНОЙ ФИЛЬТРАЦИИ. ПОРЯДКОВЫЕ СТАТИСТИКИ. РАНГОВАЯ ФИЛЬТРАЦИЯ. "БЫСТРЫЕ" АЛГОРИТМЫ РАНГОВОЙ ФИЛЬТРАЦИИ. СИГМА-ФИЛЬТР. ФИЛЬТРЫ, СОХРАНЯЮЩИЕ КРАЯ. НОРМАЛИЗАЦИЯ ФОНА.
Задача фильтрации изображений
Зашумление изображения. Модели шумов
Под задачей «фильтрации изображений» в широком смысле иногда понимают любые процедуры обработки изображений, при которых на вход процедуры подается (одно) растровое изображение, и на выходе также формируется растровое изображение. Такие процедуры типа (один растровый вход, один растровый выход) называют фильтрами.
Однако чаще под «фильтрацией» в более узком смысле понимают так называемую помеховую фильтрациюили фильтрацию изображений от «шума». При этом неявно предполагается, что первоначально где-то существовало некое «исходное» идеально чистое (незашумленное) изображение, из которого затем путемзашумления(определенного вида искажения), было получено то реальное изображение, которое мы наблюдаем. Задача помеховой фильтрации, таким образом, сводится к тому, чтобы путем некоторой обработки наблюдаемого реального изображения, как можно лучше «очистить его от шума», то есть получить изображение, наиболее близкое по своим характеристикам к исходному «незашумленному» изображению.
На самом деле необходимо понимать, что «зашумление» – это всего лишь очень упрощенная идеализированная модель возникновения искажений в цифровых изображениях реальных объектов. Вообще же говоря, искажения изображения, получаемого путем видеосъемки реального трехмерного объекта в природной обстановке, могут носить весьма сложный характер, зависящий от условий съемки (освещенность, туман, блики, тени, дождь, снег и т.п.), характеристик оптической системы (дисторсии, расфокусировки, замутненность линз и зеркал и т.п.), характеристик электронной регистрирующей аппаратуры, характеристик канала передачи, характеристик устройств оцифровки и еще многих и многих факторов. Приближенные к реальности математические модели формирования цифровых изображений содержат сотни сложных нелинейных уравнений и множество табличных поправок. При этом закон формирования значения яркости каждого пикселя изображения, как правило, не является независимым от формирования соседних пикселей, яркостные параметры изображения зависят от геометрических, и так далее. При попытке математически «скорректировать» подобную сложную модель регистрации изображения говорят уже не о фильтрации от шума, а о реставрацииилиреконструкцииизображений.
К сожалению, методы реставрации изображений слишком сложны в вычислительном смысле, чтобы на практике использоваться в системах машинного зрения, работающих в реальном масштабе времени. Кроме того, они требуют точного знания математической модели и всех параметров системы видео регистрации, что на практике также практически невозможно. Поэтому в реальных системах машинного зрения, как правило, используются более простые, но тем не менее достаточно эффективные процедуры помеховой фильтрации, разработанные для борьбы с гораздо более простыми искажениями в виде независимого зашумления пикселейизображения.
Наиболее общей моделью независимого зашумления пикселей является шум замещения. Пусть дано исходное («незашумленное») полутоновое изображениеIm, каждый пиксель которого может принимать значения в диапазоне [0..IMAX–1]. Общая модель шума замещения предполагает, что после зашумления каждый пиксель изображения, имевший ранее некотрое значение яркостиI, либо с некоторой известной вероятностьюp(I) это значение сохранит, либо данное значение яркости будет случайным образом замещено с вероятностьюq(I,J) некоторым другим значением яркостиJиз того же конечного дискретного диапазона [0..IMAX–1]. Как видно, для описания такой общей модели случайного замещения нам потребуется задать таблицупереходных вероятностейразмера (IMAX)2, что составляет весьма значительное количество в случае обычного 8-битового полутонового изображения (размер таблицы – 256256 элементов). Такое описание явно является некомпактным и поэтому редко используется на практике для полутоновых изображений. В то же время, для бинарных изображений, в которыхIMAX= 2, такое описание является наиболее удобным, простым и естественным. Чуть ниже мы еще рассмотрим модель шума замещения на бинарных изображениях – так называемую модель шума «соль и перец».
Для полутоновых изображений, как правило, рассматривают другую, более частную модель зашумления – аддитивный шум. Такая модель предполагает, что зашумленное изображение порождается по следующему закону:
Im’[x,y] = Im[x,y] + R(x,y),
где Im’[x,y] – пиксель зашумленного изображения,Im[x,y] – пиксель исходного изображения, аR(x,y) – случайнаяаддитивная шумовая компонента. Кроме того, в большинстве приложений зависимость шума от координат пикселя считается несущественной. И наконец, исходя из известного в статистикезакона больших чисел, закон распределения аддитивной шумовой компоненты предпочитают описывать удобным параметрическим семействомнормальныхилигауссовскихраспределений с нулевым средним. Таким образом,гауссовский аддитивный шумописывается следующим выражением:
Im’[x,y] = Im[x,y] + N(0,),
где N(a,) – нормальное распределение,a– математическое ожидание нормально распределенного сигнала,– средний квадрат отклонения (СКО) нормально распределенной величины. Именно такая модель зашумления чаще всего рассматривается в задачах фильтрации полутоновых изображений.
На рис. 3.2.2 – 3.2.8 показаны примеры искусственного зашумления исходного полутонового изображения лейкоцитов (рис. 3.2.1) специально сгенерированным аддитивным гауссовским шумом с различными значениями СКО. Как видно, чем больше параметр зашумления , тем более искаженным выглядит изображение. При больших значениях(рис. 3.2.7, 3.2.8) даже человеческий глаз уже с трудом различает общие очертания крупноразмерных объектов изображения (в данном случае – лейкоцитов), более мелкие и менее контрастные объекты становятся практически неразличимы.

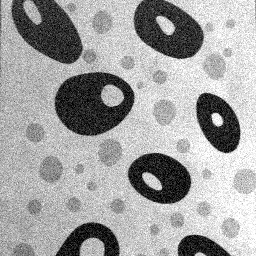
@Рис. 3.2.1. Исходное полутоновое @Рис. 3.2.2. Зашумление полутонового
изображение, = 0 изображения аддитивным гауссовским шумом,= 20


@Рис. 3.2.3. Зашумление полутонового @Рис. 3.2.4. Зашумление полутонового
изображения аддитивным гауссовским изображения аддитивным гауссовским
шумом, = 40 шумом,= 60


@Рис. 3.2.5. Зашумление полутонового @Рис. 3.2.6. Зашумление полутонового
изображения аддитивным гауссовским изображения аддитивным гауссовским
шумом, = 80 шумом,= 100


@Рис. 3.2.7. Зашумление полутонового @Рис. 3.2.8. Зашумление полутонового
изображения аддитивным гауссовским изображения аддитивным гауссовским
шумом, = 200 шумом,= 300
В следующих разделах мы будем иметь в виду этот пример, рассматривая различные методы фильтрации цифровых изображений.
