Гистограмма и гистограммная обработка изображений

Гистограммахарактеризует частоту встречаемости на изображении пикселей одинаковой яркости.

Для 8 битного полутонового изображения гистограмма яркости представляет собой одномерный целочисленный массив из 256 элементов:

Hist: 1D-array [0..255] of unsigned long (32-bit integer).

Элементы гистограммы Hist[i] содержат целые значения, равные количеству пикселей изображения, яркость которых равна значениюi. Визуально гистограмма обычно отображается как обычный график одномерной функции. Гистограмма позволяет оценить и необходимым образом изменить яркость изображения, его контраст, площадь изображения, которую занимают светлые, темные и другие яркостные элементы, и наконец, определить, где на плоскости изображения находятся отдельные области (объекты), соответствующие тем или иным диапазонам значений яркости.

Яркостными преобразованиями изображенияназываются преобразования двумерных функций яркости, описываемые простой формулой:

Im’(x,y) = f(Im(x,y)).

Здесь f(*) –функция отображения яркости, которая никак не зависит от положения пикселя (x,y). Простейшим случаем яркостных преобразований изображения являются линейные преобразования яркости, в которых функция отображения яркости имеет вид:

f(I) = a  I + b,

где a– коэффициент, определяющий изменение контраста изображения,

b– коэффициент, определяющий изменение средней яркости изображения,

I– собственно яркость в текущей точке изображенияIm(x,y). Такие линейные преобразования яркости называют такжефотографическими, так как при традиционной фотосъемке их можно устанавливать при помощи изменения характеристик выдержки и диафрагмы объектива. Возможны и другие функции отображения яркости.

Яркостные преобразования цифровых изображений часто называют гистограммными, так как при этом, во-первых, изменяется гистограмма изображения, во-вторых, вид функции преобразования (параметры преобразования) часто определяютсяадаптивно, на основании ранее собранной гистограммы исходного изображения.

В случае дискретных цифровых изображений функция отображения яркости принимает вид так называемой таблицы отображения яркостиLUT (Look-Up-Table, просмотровой таблицы).Гистограммная обработка изображения при помощи таблицы отображения яркости осуществляется следующим образом:

Im[i,j] = LUT[Im[i,j]],

где Im[i,j] – пиксель изображения с координатами (i,j), а LUT– целочисленный массив размера 256 элементов для 8 битного изображения или длиной 65536 элементов для 16-битного изображения. Далее без принципиальной потери общности будем рассматривать гистограммную обработку на примере 8-битных полутоновых изображений. При этомLUTможет задаваться:

• произвольной таблицей отображения, формируемой пользователем непосредственно;

• некоторой математической функцией, выбранной из заданного набора функций;

• адаптивно по гистограмме данного анализируемого изображения.

Пользовательские таблицы отображения позволяют выполнять следующие типовые операции:

• ручное вырезание определенных диапазонов яркости;

• ручное вырезание битовых плоскостей;

• ручная бинаризация изображения по одному или двум порогам;

• ручная сегментация изображения на несколько яркостных диапазонов.

Стандартные математические функции, используемые для формирования LUT, как правило, выделяются из следующего типового набора:

• Линейное преобразование – Linear;

• Логарифмическая функция – Log;

• Экспонента – Exp;

• Квадратичная функция – Square;

• Квадратный корень – Squareroot;

• Степенная функция – PowerX;

• Обратная степенная функция – Power1/X.

Известным частным случаем стандартной обработки изображений является инвертирование яркости, определяемое зависимостью вида

LUT[i] = 255 – i.

В результате инвертирования изображения получается его негатив. При этом темные области становятся светлыми, и наоборот.

Другое широко используемое преобразование – степенной закон вида

LUT[i] = r(i)^,

где r– коэффициент контраста, а– степень преобразования. Такие преобразования известны в области аналогового телевидения как процедурагамма-коррекции. Легко увидеть, что изменяя параметр, мы можем получатьLUTразличного типа. При

 = 1 преобразование будет линейным, при < 1 предпочтение будет отдаваться более светлым цветам (на них придется большая часть диапазона), при> 1 предпочтение будет отдаваться более темным цветам. такие преобразования часто используются для «выравнивания» яркости изображений, получаемых на электронно-лучевых трубках (ЭЛТ).

Рассмотрим теперь простейший способ адаптивной(то есть не наперёд заданной, а зависящей от данного конкретного изображения) гистограммной обработки. Начнем с линейной адаптивной процедуры, называемойяркостной нормализациейизображения и описываемой следующей математической зависимостью:

LUT[i] = 255  (i – min(Hist(Im))) / (max(Hist(Im)) – min(Hist(Im))).

Данное преобразование равномерно «растягивает» диапазон яркостей [min(Hist(Im)),max(Hist(Im))], присутствующих на исходном изображенииIm, на максимально возможны диапазон [0, 255]. Это способствует максимально возможному улучшению контраста изображения без потери каких-либо различий элементов яркости исходного изображения.

Другой популярной процедурой адаптивной гистограммной обработки изображения является эквализацияизображения. Эквализация также отображает реальный яркостной диапазон данного изображения (от минимального до максимального значения интенсивности) на диапазон [0, 255]. При этом обеспечивается «выравнивание» числа пикселей изображения, имеющих различные значения яркости. Математическая форма данного преобразования имеет вид

LUT[i] = 255  (SUM(Hist(Im),1,i) / SUM(Hist(Im),1,255),

где SUM(Hist(Im),k,i) обозначает сумму значений гистограммы изображенияImот ячейки с номеромkдо ячейки с номеромiвключительно. В тех случаях, когда в диапазоне [min(Hist(Im)),max(Hist(Im))] более или менее равномерно присутствуют все градации, визуальный эффект от эквализации изображения трудно отличить его нормализации. Однако в случае, когда значительная часть градаций яркости отсутствует, эквализация позволяет более равномерно использовать диапазон [0, 255] для более контрастного отображения присутствующих на изображении градаций. Визуально это выглядит как «проявление» большего количества ранее незаметных на изображении деталей и контуров.

В заключение этого краткого введения в гистограммную обработку и анализ изображений необходимо отметить, что наиболее общей смысловой единицей анализа гистограммы является мода. Это понятие, позаимствованное из математической статистики, означает максимум или «горб» графика гистограммы. Если гистограмма имеет одну моду, такая гистограмма называетсяунимодальнойи свидетельствует о яркостной однородности изображения.Бимодальнаягистограмма с двумя явно наблюдающимися модами, разделенными заметной «впадиной», скорее всего означает, что данное изображение содержит заметно отличающиеся друг от друга «светлую» и «темную» области, часто называемые «фоном» и «объектом» или «фоном» и «символом». Разделение этих областей порогом, определяемым по гистограмме, называетсяадаптивной бинаризацией изображения. Наконец, если на гистограмме наблюдается несколько мод, такая гистограмма называетсямультимодальной, и ее анализ осуществляется более сложными методами.

Рассмотрим теперь, как гистограммные преобразования яркости реализуются в среде Pisoft.

Рис.2.1. Средство построения и анализа гистограммы

Рис.2.2. Средство построения и анализа проекций

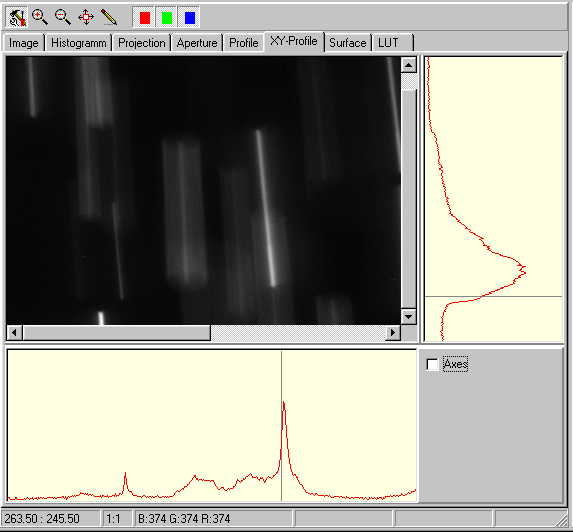
Рис 2.3. Средство построения и анализа профилей

 

Рис.2.4. Средство построения и анализа профиля вдоль произвольной кривой

Рис.2.5 Средство для табличных преобразований яркости

Рис.2.6 Пример задания табличного преобразования яркости