3. Исходные данные

Параметры орбиты ИСЗ – варьируемые:

Долгота восходящего узла: ;

Наклонение орбиты: ;

Широта перицентра: .

Большая полуось орбиты: км

Эксцентриситет:

Истинная аномалия на начало эксперимента: .

1. Порядок выполнения

1. Выбрать параметры орбиты ИСЗ в оскулирующих элементах, пересчитать их в геоцентрические прямоугольные координаты с целью формирования начальных условий интегрирования.

2. Реализовать четыре математических модели движения ИСЗ с использованием каждой из перечисленных моделей гравитации (используя информацию, содержащуюся в [1]).

3. Используя метод численного интегрирования, провести четыре вычислительных эксперимента, состоящих в моделировании движения ИСЗ при одинаковых начальных условиях и разных моделях гравитации.

5. Методические указания к выполнению работы

В справочнике [1] приведены соотношения, описывающие гравитационный потенциал Земли тремя разными способами: с использованием точечных масс («нормальное поле в точечных массах»), разложением в ряд по сферическим функциям (т.н. «нормальное поле в сферических функциях») и с использованием аномальных поправок (т.н. «аномальное поле в сферических функциях»). Для получения ускорений ИСЗ в геоцентрической прямоугольной СК необходимо вычислить частные производные потенциала по соответствующим координатам. Для моделей нормального и аномального поля, полученных разложением в ряд по сферическим функциям, выражение для потенциала определено в сферических координатах (), поэтому для использования выражений его производных в правых частях дифференциальных уравнений необходимо выполнить их пересчет в геоцентрическую прямоугольную СК.

1. Центральное поле Земли

,

где м³/с²– геоцентрическая гравитационная постоянная;

– радиус-вектор ИСЗ в прямоугольной геоцентрической СК.

2. Нормальная Земля в точечных массах

;

,

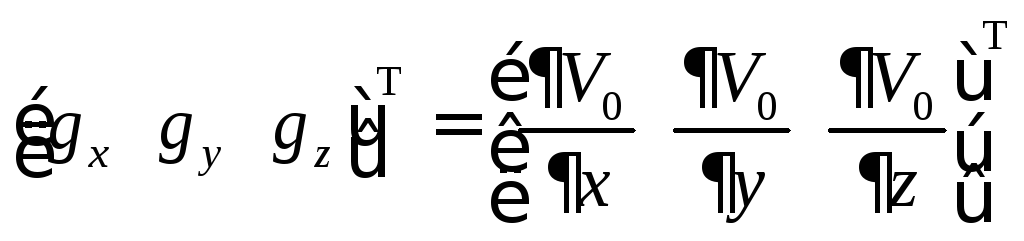где – потенциал притяжения нормальной Земли в точечных массах:

, где:

– отношение-ой точечной массы к массе Земли (см. [1]);

– расстояние от-ой точечной массы до текущей точки (положение ИСЗ).

– количество используемых точечных масс.

3. Нормальная Земля в сферических функциях

;

Потенциал притяжения нормальной Земли, согласованный с параметрами общего земного эллипсоида (ОЗЭ):

,

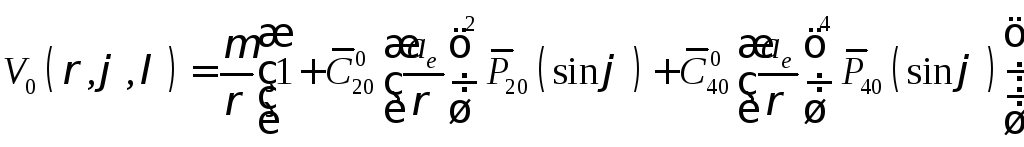где () – сферические координаты текущей точки;

м – большая полуось ОЗЭ.

;

;

,– полностью нормированные полиномы Лежандра второй и четвертой степеней (см.[1]).

4. Аномальная Земля в сферических функциях

;

Потенциал притяжения аномальной Земли:

,

где () – сферические координаты текущей точки;

,– коэффициенты разложения гравитационного поля Земли по сферическим функциям (приведены в [1]);

– количество членов ряда, участвующих в разложении ()

Алгоритмы расчета нормированных функций Лежандра и их производных рассмотрен в [1] (требуется их программная реализация).

Пересчет ускорений (производных гравитационного потенциала) из сферических координат в геоцентрические прямоугольные должен выполняться с использованием переходной матрицы:

,

где – длина радиус-вектора текущей точки (положения ИСЗ);

– длина проекции радиус-вектора текущей точки (положения ИСЗ) на плоскость ;

– гравитационные ускорения в сферических координатах (частные производные гравитационного потенциала).

Для перехода от сферических координат к прямоугольным следует использовать соотношения:

Обратный переход может быть выполнен с использованием соотношений: