Математическая модель движения исз созвездия.

Математическая модель центра масс ИСЗ созвездия как материальной точки имеет следующий вид:

,

где:

m- масса ИСЗ,

X- вектор состояния ИСЗ,

F_i- силы, действующие на ИСЗ.

Таким образом, точность моделирования динамики ИСЗ созвездия зависит только от состава учитываемых возмущений. Пользователь может учитывать по своему усмотрению следующие возмущения:

• силы, вызванные гравитационным влиянием Земли с учетом ее несферичности;

• силы, вызванные гравитационным влиянием Луны и Солнца;

• аэродинамические силы;

• силы, вызванные давлением солнечного света без учета переотражения и альбедо;

• силы, вызванные управляющими ускорениями.

Математические модели перечисленных возмущающих факторов, используемых в МДС, приведены ниже.

Модель геопотенциала

Для представления геопотенциала используется его разложение в ряд по шаровым функциям [3]:

,

где

R_- экваториальный радиус Земли;

r- величина геоцентрического радиус-вектора рассматриваемой точки пространства;

, - геоцентрические широта и долгота точки;

P_n^m- присоединенная функция Лежандра;

C_n,m, S_n,m- константы.

Для вычисления градиента геопотенциала в ГСК используется так называемый алгоритм Каннингхема. Основная идея этого алгоритма состоит в комплексном представлении геопотенциала, что позволяет выделить компоненты, зависящие только от координат данной точки пространства (так называемые V_n,mфункции):

,

В результате геопотенциал может быть представлен в виде:

,

и необходимые для расчетов гравитационные ускорения определяются следующим образом:

.

Окончательно получаем:

,

,

,

где V*- величина, сопряженная сV.

Рекуррентные формулы для вычисления V_nmимеют следующий вид:

,

,

.

Приведенные выше соотношения для V_n,mдают эффективный вычислительный алгоритм определения компонент гравитационного ускорения в ГСК. Это дает возможность сократить время вычислений, поскольку в процессе численного интегрирования уравнений движения ИСЗ необходимо неоднократно вычислять гравитационные ускорения на каждом шаге интегрирования.

Гравитационное влияние Луны и Солнца

Для вычисления гравитационных ускорений, вызываемых влиянием Луны и Солнца используется традиционная математическая модель, описанная например в [4]. Если геоцентрическое положение Луны и Солнца известно, то соответствующие ускорения определяются следующим образом:

,

,

,

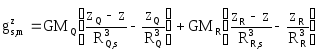где (X_Q,Y_Q,Z_Q) - геоцентрические координаты Солнца;

(X_R,Y_R,Z_R) - геоцентрические координаты Луны.

Основная проблема здесь состоит в необходимой точности определения геоцентрического положения Луны и Солнца на требуемый момент времени. Исходные данные относительно положения Луны и Солнца подготавливаются на основе теории DE2000/LE200 [4], которая считается в настоящее время наиболее точной. Эта теория используется также для расчета параметров прецессии и нутации. Для того, чтобы уменьшить время вычисления положений Луны и Солнца на требуемый момент времени с необходимой точностью, обсуждаемое ПМО использует Чебышевскую аппроксимацию исходных данных по геоцентрическому положению этих светил.

Аэродинамические силы

Опыт космических исследований показывает [2], что для большинства орбит необходимо учитывать только ту составляющую аэродинамической силы, которая противоположна по направлению вектору относительной скорости ИСЗ. Эта сила является силой аэродинамического сопротивления и определяется следующим образом:

,

где

 - плотность атмосферы;

V- скорость ИСЗ относительно атмосферы;

m- масса ИСЗ;

A- опорное значение площади ИСЗ для расчета сопротивления;

C_D- коэффициент аэродинамического сопротивления ИСЗ.

Величина C_D зависит главным образом от двух факторов: средней длины пробега молекул воздуха в атмосфере и геометрических размеров ИСЗ. Как правило, величинаC_Dдля данного ИСЗ должна быть известна заранее. Опорное значение площади ИСЗ, используемое для расчета аэродинамического сопротивления зависит от ориентации ИСЗ и, следовательно, является переменной величиной. Заметим, что в тех случаях, когда не рассматривается движение ИСЗ вокруг центра масс, при моделировании аэродинамической силы целесообразно использовать произведениеAC_D, которое уточняется затем по результатам навигационного эксперимента как компонента расширенного вектора состояния ИСЗ.

Наиболее сложной и важной проблемой при моделировании и расчете аэродинамической силы является выбор модели атмосферы или, более конкретно, модели зависимости плотности от высоты полета (h). Программа МДС использует “Модель плотности для баллистического обеспечения полетов искусственных спутников Земли” (ГОСТ 25645.115-84). В соответствии с этой моделью плотность атмосферы определяется следующим образом:

 = _нК₀К₁К₂К₃К₄,

где:

_н- ночная плотность атмосферы -_н= 9.80665exp{a₁-a₂(h-a₃)^1/2}

h- высота полета ИСЗ,

a₁, a₂, a₃- коэффициенты,

К₀- коэффициент, учитывающий вариации плотности, вызванные средневзвешенным значением коэффициента солнечной активности,

К₁- коэффициент, учитывающий суточный эффект перераспределения плотности,

К₂- коэффициент, учитывающий полугодовой эффект перераспределение плотности,

К₃- коэффициент, учитывающий вариации плотности, определяемые отклонением коэффициента солнечной активности от средневзвешенного значения

К₄- коэффициент, учитывающий зависимость плотности атмосферы от геомагнитной активности.

Детальное описание способа вычисления упомянутых коэффициентов приводится в [7].

Давление солнечного света

Математическая модель ускорения g_sp, вызванного давлением солнечных лучей, определяется следующим образом:

,

где

k= 4.56´10-6 N/m²- давление солнечных лучей в окрестности земной орбиты;

A= 1.4959787061´10¹¹- астрономическая единица;

S- площадь облучаемой поверхности ИСЗ;

m- масса ИСЗ;

C_R- коэффициент отражения;

, R- геоцентрический радиус-вектор ИСЗ и его модуль соответственно (в случае, если ИСЗ не затеняется Луной или Землей).

Управляющие ускорения

Математическая модель управляющего ускорения может быть построена в случае, если имеется достаточно подробная модель тяги бортовой корректирующей двигательной установки.

Математическая модель вектора ускорения g_сtl, вызываемого корректирующим импульсом тяги имеет вид:

g_ctl = P/m,

где

P- вектор тяги;

m- текущая масса ИСЗ.

Здесь мы полагаем, что ИСЗ оборудован двигательной установкой малой тяги с фиксированным уровнем тяги. В случае необходимости программа МДС позволяет моделировать работу установки малой тяги на заданном интервале времени.При этом программа МДС использует специальную технологию, которая позволяет отслеживать моменты включения и выключения установки малой тяги с целью высокоточного интегрирования уравнений движения ИСЗ путем автоматического выбора шага интегрирования (подробнее смотри ниже).