Рулевой привод элеронов

ДУС

Корректирующее

устройство

Уравнения углового движения ла по крену

(-)

Рис. 3.3. Состав и структура системы стабилизации в канале крена

Измерительные устройства системы стабилизации

В составе системы стабилизации используется измерительные устройства трех типов:

• датчик угловых скоростей (ДУС);

• датчик линейных ускорений (акселерометр);

• датчик угла атаки.

Датчик угловых скоростей

Датчик угловых скоростей (ДУС) осуществляет измерения угловой скорости в связанной системе координат.

Динамические свойства ДУС описываются передаточной функцией колебательного звена и звеном типа «насыщение» с уровнем .

Передаточная функция ДУС является следующей:

, (3.1)

где :

- угловая скорость на входе скоростного гироскопа;

- выходной сигнал гироскопа;

и - постоянная времени и коэффициент демпфирования колебательного звена, которым описываются динамические свойства скоростного гироскопа

- уровень насыщения (диапазон измерений) гироскопа.

Указанным передаточной функции и звену «насыщение» соответствует система дифференциальных уравнений в нормальной форме Коши:

, (3.2)

где:

- вспомогательные переменные, которые используются для описания динамики датчика в виде уравнения 2-го порядка в нормальной форме Коши.

Уравнения гироскопа присутствуют в полной системе уравнений 3 раза для трех датчиков, измеряющих .

Акселерометр

Нормальные ускорения ЛА измеряются датчиком линейных ускорений (акселерометром) в связанной системе координат.

Математическая модель датчика линейных ускорений (ДЛУ) аналогична модели ДУС. Динамика датчика описывается колебательным звеном и нелинейным звеном типа «насыщение» с уровнем насыщения .

Передаточная функция акселерометра задается соотношением:

, (3.3)

где:

- перегрузка, измеряемая акселерометром;

- сигнал на выходе акселерометра;

и - постоянная времени и коэффициент демпфирования колебательного звена, которым описываются динамические свойства акселерометра;

- уровень насыщения (диапазон измерений) акселерометра.

В нормальной форме Коши динамика акселерометра описывается следующими уравнениями:

, (3.4)

где:

- вспомогательные переменные, которые используются для описания динамики датчика в виде уравнения 2-го порядка в нормальной форме Коши.

Уравнения акселерометра присутствуют в полной системе уравнений 2 раза для двух датчиков, измеряющих .

Измеритель угла атаки

Для измерения угла атаки на ЛА рассматриваемого класса применяются флюгерные датчики, расположенные на корпусе ЛА впереди аэродинамических рулей.

Математическая модель датчика аналогична моделям ДУС и ДЛУ. Она представлена колебательным звеном и звеном типа «насыщение» с уровнем насыщения .

Передаточная функция датчика угла атаки имеет вид:

(3.5)

где:

- угол атаки, измеряемый датчиком;

- сигнал на выходе датчика;

и - постоянная времени и коэффициент демпфирования колебательного звена, которым описываются динамические свойства датчика угла атаки;

- уровень насыщения датчика угла атаки.

Динамика датчика угла атаки описывается уравнениями:

, (3.6)

где:

- вспомогательные переменные, которые используются для описания динамики датчика в виде уравнения 2-го порядка в нормальной форме Коши.

Уравнения присутствуют в полной системе уравнений 2 раза для двух датчиков, измеряющих .

Корректирующие устройства контуров системы стабилизации

Как видно из блок-схемы продольного канала системы стабилизации (см. рис. 3.2), в ней используются два корректирующих устройства:

• устройство в замкнутом контуре;

• устройство в прямой цепи.

а) Корректирующее устройство

Сигнал наведения , сформированный в цепи формирования сигнала наведения, перед подачей его в замкнутый контур системы стабилизации подвергается нелинейному преобразованию с помощью устройства переменной структуры. Цель преобразования – ограничить угол атаки ЛА.

Преобразование сигнала осуществляется с помощью соотношения:

(3.7)

В этом соотношении:

- командный сигнал, поступающий в систему стабилизации из системы наведения (см. рис. 3.2);

- выходной сигнал устройства ;

(3.8)

- максимально допустимое значение угла атаки;

- эмпирическая функция, которая имеет следующую структуру:

(3.9)

- измеренное датчиком угла атаки значение угла атаки в канале;

- угловая скорость ЛА в канале, измеренная с помощью ДУС;

- угловое ускорение ЛА в канале, вычисляемое при помощи соотношения:

- производная перегрузки ЛА в канале, определяемая при помощи соотношения:

- коэффициенты;

- постоянные времени интегро-дифференцирующего фильтра 1-го порядка;

- постоянные времени измерителей углового ускорения и производной перегрузки ЛА в канале.

В нормальной форме Коши соотношение (3.9) записывается следующим образом:

(3.10)

где:

- вспомогательные переменные;

Уравнения для изаписываются следующим образом:

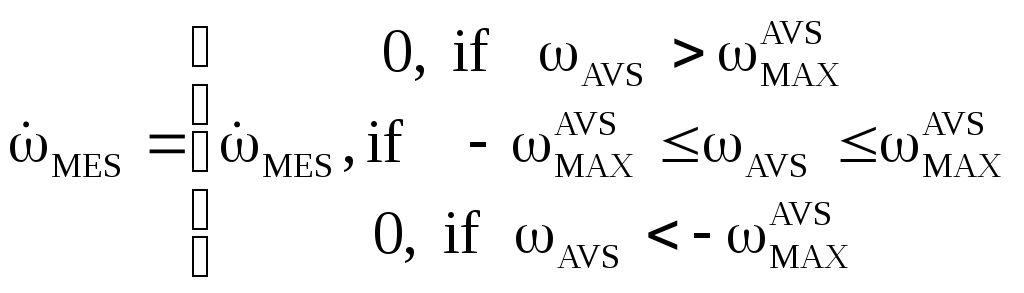
где:

- вспомогательные переменные.

Здесь также необходимо учитывать, что коэффициенты ,заданы исходя из условия, чтоизадаются в град/с и град/с² соответственно. Также в градусах задается величина - угол атаки, измеренный датчиком угла атаки.

б) Корректирующее устройство

Это корректирующее устройство реализует нелинейный закон стабилизации (т.е. представляет собой регулятор с переменной структурой).

Закон стабилизации формируется следующим образом:

(3.11)

где

- сигнал на выходе корректирующего устройства, требуемое значение угла отклонения рулей;

- угловая скорость ЛА в канале, измеренная с помощью ДУС;

- угловое ускорение ЛА в канале, вычисляемое при помощи соотношения:

- разность между потребной перегрузкой ЛА, сформированной в корректирующем устройстве (во входной цепи контура) и перегрузкой, измеренной с помощью акселерометра;

- передаточные коэффициенты по перегрузке, угловой скорости и угловому ускорению ЛА;

- постоянные времени интегро-дифференцирующего звена;

- функция переключения, равная нулю или единице в зависимости от значения аргумента .

Переменная , входящая в выражение (3.11), рассчитывается с использованием следующего соотношения:

, (3.12)

где:

- заданные коэффициенты;

- постоянная времени апериодического звена.

В нормальной форме Коши соотношения (3.11) и (3.12) можно переписать следующим образом:

(3.13)

где:

- вспомогательные переменные;

Совместно уравнения (3.11) и (3.12) описывают работу корректирующего устройства .

Необходимо учитывать, что коэффициенты ,,,заданы исходя из условия, чтоизадаются в град/с и град/с² соответственно.

Как показано на схеме рис. 3.3, в контуре стабилизации угловой скорости крена используется корректирующее устройство .

Это устройство имеет следующую структуру:

(3.14)

где:

- сигнал на выходе корректирующего устройства, требуемое значение угла отклонения элеронов;

- угловая скорость крена, измеренная ДУС.

- коэффициент усиления и постоянные времени фильтра.

В нормальной форме Коши соотношения (3.14) можно переписать следующим образом:

(3.15)

где:

- вспомогательные переменные;

Рулевые приводы

Структура и характеристики рулевого привода в каждом из двух продольных каналов задаются математической моделью, показанной на рис. 3.4.

1

K_G

( - )

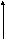
Рис. 3.4. Состав и структура рулевого привода в продольных каналах

На этой схеме:

- максимальная скорость поворота рулей в продольном канале;

- максимальный угол поворота аэродинамических рулей;

K_G– коэффициент пропорциональности между углами отклонения аэродинамического и газового рулей.

Как видно на схеме, управление аэродинамическими и газовыми рулями происходит с помощью единого рулевого привода и углы поворота обоих рулей пропорциональны друг другу. Коэффициент пропорциональности определяется из соотношения:

,

где и- максимально возможные углы отклонения соответственно газовых и аэродинамических рулей.

В прямой цепи рулевого привода находится апериодическое звено:

.

Этому звену соответствует дифференциальное уравнение первого порядка:

(3.16)

где: - коэффициент усиления (добротность) рулевого привода.

Дополнительно к уравнению (3.16), динамика рулевого привода в продольных каналах описывается следующими уравнениями:

(3.17)

.

В этих уравнениях:

- индекс, обозначающий рулевой привод в продольных каналах;

и - углы поворота аэродинамических и газовых рулей;

- уровни насыщения по угловой скорости и углу поворота рулей;

- переменные, которые используются для описания динамики рулевого привода в виде уравнения в нормальной форме Коши: сигнал на выходе апериодического звена и переменная на выходе интегрирующего звена, соответственно.

Уравнения (3.16) - (3.17) присутствуют в полной системе уравнений 2 раза для двух приводов, функционирующих в продольных каналах I и II.

Привод элеронов в канале крена

Состав и структура рулевого привода в канале крена аналогичны приводу в продольных каналах (рис. 3.5). Различие состоит в том, что привод в канале крена управляет положением только аэродинамических органов управления – элеронов, а также в конкретных значениях параметров привода .

( - )

Рис. 3.5. Состав и структура рулевого привода в канале крена

В прямой цепи рулевого привода находится апериодическое звено:

.

Этому звену соответствует дифференциальное уравнение первого порядка:

(3.18)

где: - коэффициент усиления (добротность) рулевого привода.

Дополнительно к уравнению (3.18), динамика рулевого привода в канале крена описывается следующими уравнениями:

(3.19)

В этих уравнениях:

- индекс, обозначающий рулевой привод в канале крена;

- углы поворота элеронов;

- уровни насыщения по угловой скорости и углу поворота рулей;

- переменные, которые используются для описания динамики рулевого привода в виде уравнения в нормальной форме Коши: сигнал на выходе апериодического звена и переменная на выходе интегрирующего звена, соответственно.

Методика моделирования

При моделировании управляемого движения ЛА вся совокупность дифференциальных уравнений, описывающих динамику системы стабилизации (3.2, 3.4, 3.6, 3.8, 3.10, 3.13, 3.153.19), включаются в общую систему уравнений движения ЛА, описанных в п.2 настоящего документа. При этом размерность фазового вектора увеличивается до 47. Коэффициент веса в методе интегрирования для уравнений системы стабилизации выбран равным 1000, т.е. таким как и коэффициент для уравнений углового движения.

МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ЦЕЛИ

При рассмотрении процесса наведения ЛА необходимо моделировать движение цели с различными видами маневров. Для этого ниже рассматривается технология моделирования движения и основные виды маневров цели.

Уравнения движения цели

Рассматривается пространственное движение цели как тела с тремя степенями свободы. Обозначим вектор скорости цели в ИСК как . Этот вектор задается его модулеми двумя траекторными углами:. Проекции вектора скорости целина оси ИСК описываются уравнениями:

(4.1)

Маневрирование цели задается тремя составляющими ее ускорения относительно ее вектора скорости:

. (4.2)

Из приведенных соотношений следует, что:

• при нулевых углах ии при нулевых ускоренияхцель совершает горизонтальный полет с постоянной скоростью параллельно осив направлении начала координат, т.е. сближается с ЛА;

• при отрицательных значениях угла цель совершает прямолинейное движение в сторону ЛА со снижением высоты поелета;

• при цель совершает маневр по скорости;

• при цель совершает маневр в вертикальной плоскости, при этом положительное ускорение вызывает набор высоты, а отрицательное –снижение высоты полета цели;

• при цель совершает маневр в горизонтальной плоскости;

• при одновременном действии ускорений в вертикальной и горизонтальной плоскостях цель соверщает пространственный маневр.

Виды маневров

Конкретный способ маневрирования цели определяется способом задания составляющих ускорений цели как явных функций времени:

Обычно рассматривают следующие типовые маневры:

Односторонний маневр в одной плоскости. Происходит с момента с постоянным ускорениемилив течение заданного интервала времени. Например, односторонний горизонтальный маневр на интервале временизаписывается так:

(4.3)

Обычно момент начала маневра выбирается так, чтобы маневр длился до точки встречи с целью.

Уравнение для одностороннего вертикального маневра записывается аналогично.